Quiz Master No : 224 Answers

Question No : 01

එක් කොටසක් භ්‍රමණය කළ විට ඉස්කුරුප්පුව චලනය වන දුර    = a/n mm

කොටස් x ගණනක් භ්‍රමණය කළ විට ඉස්කුරුප්පුව චලනය වන දුර = ax/n mm

කොටස් x ගණනක් භ්‍රමණය කළ විට ඉස්කුරුප්පුව චලනය වන දුර ax/n mm වේ.

Question No : 02

a) සිදු වේ.

මෙහි දී වස්තුවේ ස්කන්ධය m ලෙස සලකමු. වස්‍තුවේ සිරස් සමතුලිතතාවය ගත් විට, mg + F₂ = R වේ. මෙහි දී F₂ බලය වැඩි කරන විට වස්තුව මත ඇති වන අභිලම්භ ප්‍රතික්‍රියාව වැඩි වේ.

b) සිදු නොවේ.

වස්තුව චලනය නොවන බැවින් වස්තුව මත ඇති වන ඝර්ෂණ බලය බාහිර බලයට සමාන වේ. එනම් වස්තුව මත යෙදෙන තිරස් F₁ බලයට වේ. මෙහිදී F₂ බලය වැඩි කරන විට වස්තුව හා තලය අතර ඇතිවන ඝර්ෂණ බලය වැඩි නොවේ.

c) සිදු වේ.

වස්තුව හා තලය අතර ඇතිවන උපරිම ඝර්ෂණ බලය μR ට සමාන වේ. මෙහි දී F₂ බලය වැඩි කරන විට වස්තුව මත ඇති වන අභිලම්භ ප්‍රතික්‍රියාව R වැඩි වේ. එම නිසා වස්තුව මත ඇති වන උපරිම ඝර්ෂණ බලය වැඩි වේ.

මෙහි දී a හා c යන්න පමණක් සිදු වේ.  

Question No : 03

එක් වස්තුවක ස්කන්ධය m ලෙස සලකමු. 

පහළින් පවතින ස්කන්ධයේ සමතුලිතතාවය සැලකු විට, 

T = mg

මෙහි දී තන්තුව කැපූ මොහොතේ දී දුන්නේ විතතිය වෙනස් නොවන බැවින් දුන්නේ ප්‍රත්‍යස්ථ බලය වෙනස් නොවේ. 

තන්තුව කැපු විට ඉහළින් පවතින වස්තුව සලකා 

F      = ma 

T + mg = ma

2mg    = ma 

a      = 2g

තන්තුව කැපූ මොහොතේ දී ඉහළ පවතින වස්තුවේ ත්වරණය 2g වේ.

Question No : 04

T = 2π/ω  

ω = 2π/2  

ω = π

ω = 3 rads⁻¹  

a = ω²x  

වස්තුව උපරිම ත්වරණය ලබා ගන්නේ විස්ථාරයේ දී වේ. මෙහි දී A හා B යන ලක්ෂ්‍යය දෙක අතර පරතරය 4 m වේ. එබැවින් විස්ථාරය 2 m වේ. 

a = ω²A

a = (3 rads⁻¹)²⨯2 m

a = 18 ms⁻² 

F = ma 

F = 0.2 kg⨯18 ms⁻² 

F = 3.6 N 

වස්තුව මත යෙදෙන උපරිම බලය 3.6 N වේ.

Question No : 05

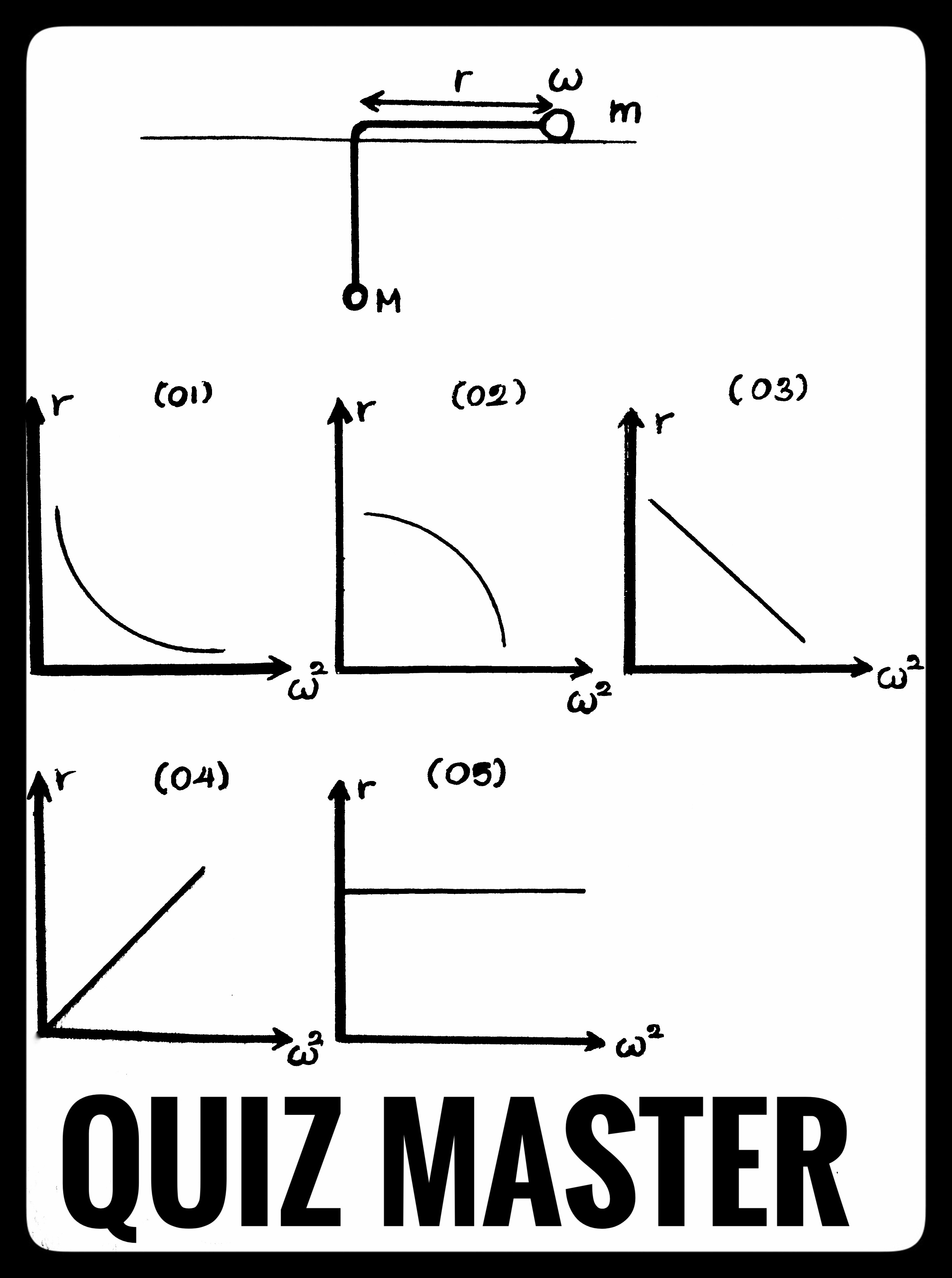
මෙහි දී M ස්කන්ධයේ සමතුලිතතාවය සැලකු විට,

T = Mg 

m ස්කන්ධය සලකා කේන්ද්‍රය දෙසට F = ma යෙදීමෙන්,

T = mω²r

Mg = mω²r

r = Mg/mω²

ඒ අනුව ω² සමග r වෙනස් වන ආකාරය නිවැරදිව දැක්වෙන්නේ, 1) හි දැක්වෙන ප්‍රස්ථාරය මගින් ය.