Puzzle #87. Новости

Разбор

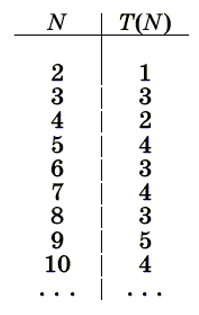
Обозначим через T(n) минимальное время, за которое n друзей смогут обменяться новостями. Любопытно, что функция T = T(N) не монотонна. Это можно обнаружить, найдя значения T(N) для небольших N — они приведены в таблице ниже.

Рассмотрим произвольную новость. После первого часа её знают не больше двух друзей, после второго часа — не больше четырёх друзей, ..., после k-го часа — не больше 2^k друзей. Поэтому, если после T часов все N друзей знают все новости, то 2^T ≥ N и T ≥ log2(N). 

Так как T — целое число, то T ≥ [log2(N)] (Значение логарифма округляем в большую сторону).

Если N — нечётное число, то найдётся один из N друзей — обозначим его через A, — который в первый час не участвует в разговорах. Применяя вышеприведённые рассуждения к той новости, которую вначале знает только A, мы получим, что для обмена всеми новостями необходимо не менее 1 + log2(N).

По этой формуле получаем следующие ответы:

• а) [log2(64)] = 6 часов 
• б) 1 + [log2(55)] = 7 часов 
• в) [log2(100)] = 7 часов.