Проверка статистических гипотез

Итак, начнём с того, что есть нулевая гипотеза (Н0). В общем смысле она гласит, что между событиями нет разницы. Например, при проверке распределения на нормальность нулевая гипотеза будет о том, что между распределением нашей выборки и нормальным разницы нет. При сравнении групп (например эксперимент vs контроль) нулевая гипотеза может быть, например в том, что между математическим ожиданиями генеральных совокупностей, откуда пришли выборки, разницы нет. Также есть альтернативная гипотеза (Н1), она прямо противоположна нулевой и говорит, что различия есть.

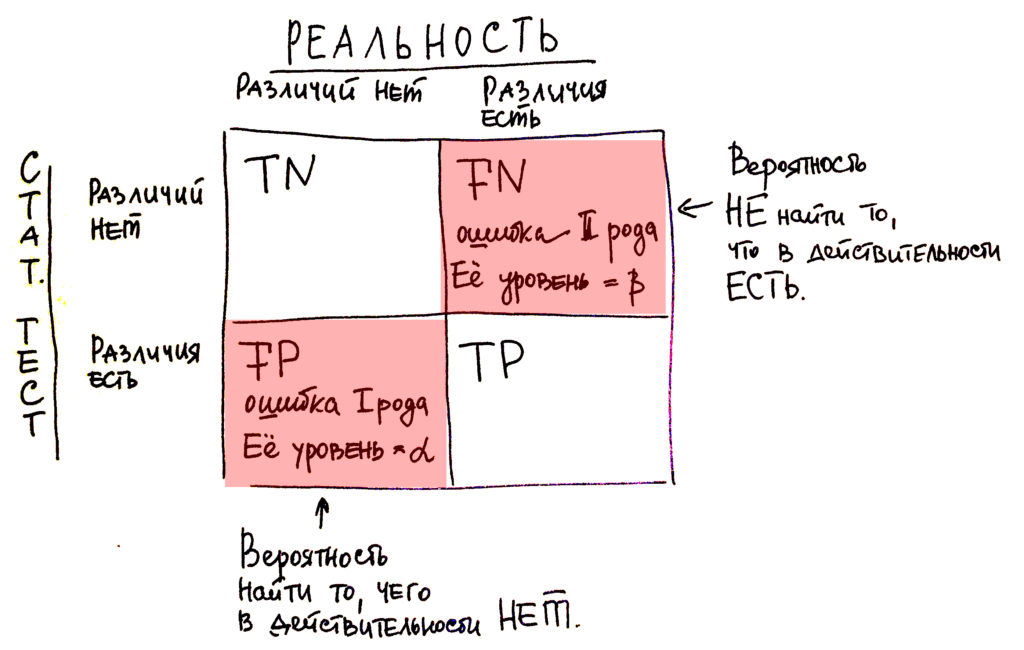
Проверка статистических гипотез по сути сводится к отвержению или принятию нулевой гипотезы. Мы задаём некоторые условия, при которых считаем, что верна либо Н0, либо Н1. Но всегда есть вероятность, что мы ошибёмся. Если мы отвергаем Н0 при условии, что на самом деле она верна, то мы совершаем ошибку I рода. Её вероятность называется называется уровнем значимости (α). Если мы принимаем Н0, хотя она не верна, то мы совершаем ошибку II рода, а её вероятность обозначается буквой β. Она нам ещё понадобится в разговоре про мощность критерия.

Теперь немного о логике проверки гипотез. Сначала мы предполагаем, что нулевая гипотеза верна. Исходя из этого предположения определяется статистика критерия - это некоторая функция, отличающаяся для разных критериев. Как и любая функция, статистика может иметь разное распределение вероятностей, и для многих критериев оно стандартное нормальное или Стьюдента.

На хвостах распределения мы находим некоторую критическую область такую, чтобы вероятность попадания в неё значения статистики не превышала уровень значимости α. Чаще всего α принимают за 0.05 или 0.01. Критическая область бывает односторонней (лево- и право-) и двухсторонней и это зависит от альтернативной гипотезы. Если мы говорим, что что-то просто отличается, не важно в большую или меньшую сторону, то используем двухстороннюю критическую область. А если мы в альтернативную гипотезу вшиваем, что, например, одна выборка заведомо больше или меньше другой, то тогда критическая область будет односторонней.

Далее мы высчитываем значение статистики для конкретно нашей выборки. Чем оно больше, тем ближе к хвостам распределения оно будет лежать, и рано или поздно мы попадём в критическую область. И как только значение статистики будет там - мы говорим, что отвергаем нулевую гипотезу на уровне значимости α.

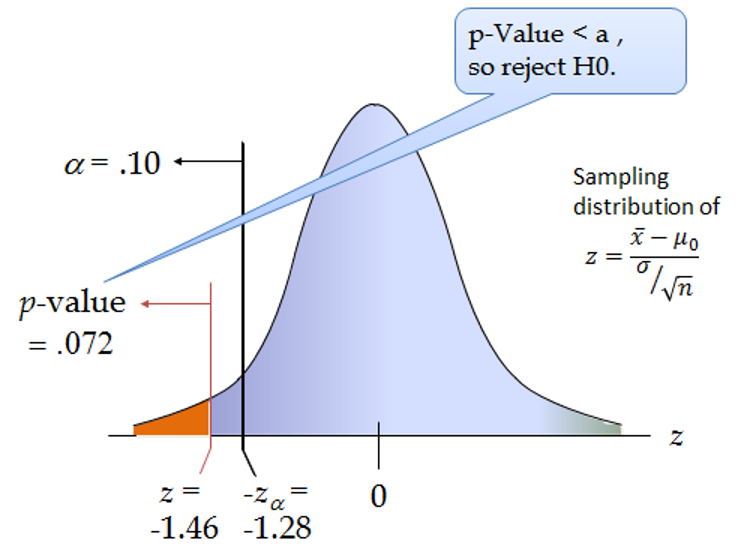
Различные программы выдают нам результаты расчёта статистик, но пользоваться ими не удобно, так как нам надо искать конкретные точки на оси Х, отсекаемые критической областью и сравнивать с ними. Поэтому помимо конкретного значения, рассчитывается также вероятность получения такого же или ещё большего по модулю значения статистики. И эта вероятность называется p-значением. Поскольку мы уже знаем, что в критической области вероятность значений не может превышать уровень значимости, то если наша выстраданная в эксперименте вероятность a.k.a. p-значение меньше этого уровня, то она явно будет в критической области. А если мы в критической области, то H0 отвергается. Собственно в этом и кроется суть заветного р<0.05.

Ещё раз

Если p>α, то принимаем Н0 и различий нет, если p<α, то принимаем H1 и различия есть.

И я пишу именно α, а не 0.05. Уровень значимости мы задаём сами, можем хоть единицей сделать, хотя тогда 100% совершим ошибку 1 рода. Так что все договорились, что 0.05 или на крайняк 0.01 будет  ̶с̶о̶м̶н̶и̶т̶е̶л̶ь̶н̶о̶,̶ ̶н̶о̶ ок. И вот какая штука, мы сначала сами поставили границу, а потом получили, что если у нас p=0.051, то различий нет, а если р=0.049, то различия есть. Разница мизерная, а результат диаметрально противоположный. Поэтому p-значение в частности и весь описываемый в классических учебниках подход к статистике всё чаще подвергается критике и в качестве альтернативы рассматривается байесовская статистика. Особенно активно это развивается для областей, связанных с работой с большими данными и машинным обучением. Очень понравилась вот эта статья на Хабре, в котором эта проблема отражена в диалоге между байесовцем и учёным.

Тем не менее во многих областях науки от p-значения уйдут ещё не скоро, так что в следующих постах я расскажу о том, что делать если p>0.05 и почему p<0.05 не всегда повод для радости.