Простой тест на простоту

TL;DR: Тест на простоту, который легче запомнить, написать и доказать, чем тест Миллера — Рабина

Если в задаче нужно проверить на простоту достаточно большое число n, скорее всего вы будете делать это при помощи теста Миллера — Рабина. Не знаю как вы, но я постоянно забываю, как его писать. Он не интуитивно понятный! И доказывать его достаточно сложно.

С другой стороны, тест Ферма очень простой и понятный: берем кучу случайных чисел a, не равных нулю, и проверяем, что a^(n-1) дает остаток 1 от деления на n. Однако, как известно, этот тест не работает на числах Кармайкла. Тест, который я нашел в одной статье 1982 года, почти так же прост, однако работает для любых чисел. Не буду томить и сразу покажу его:

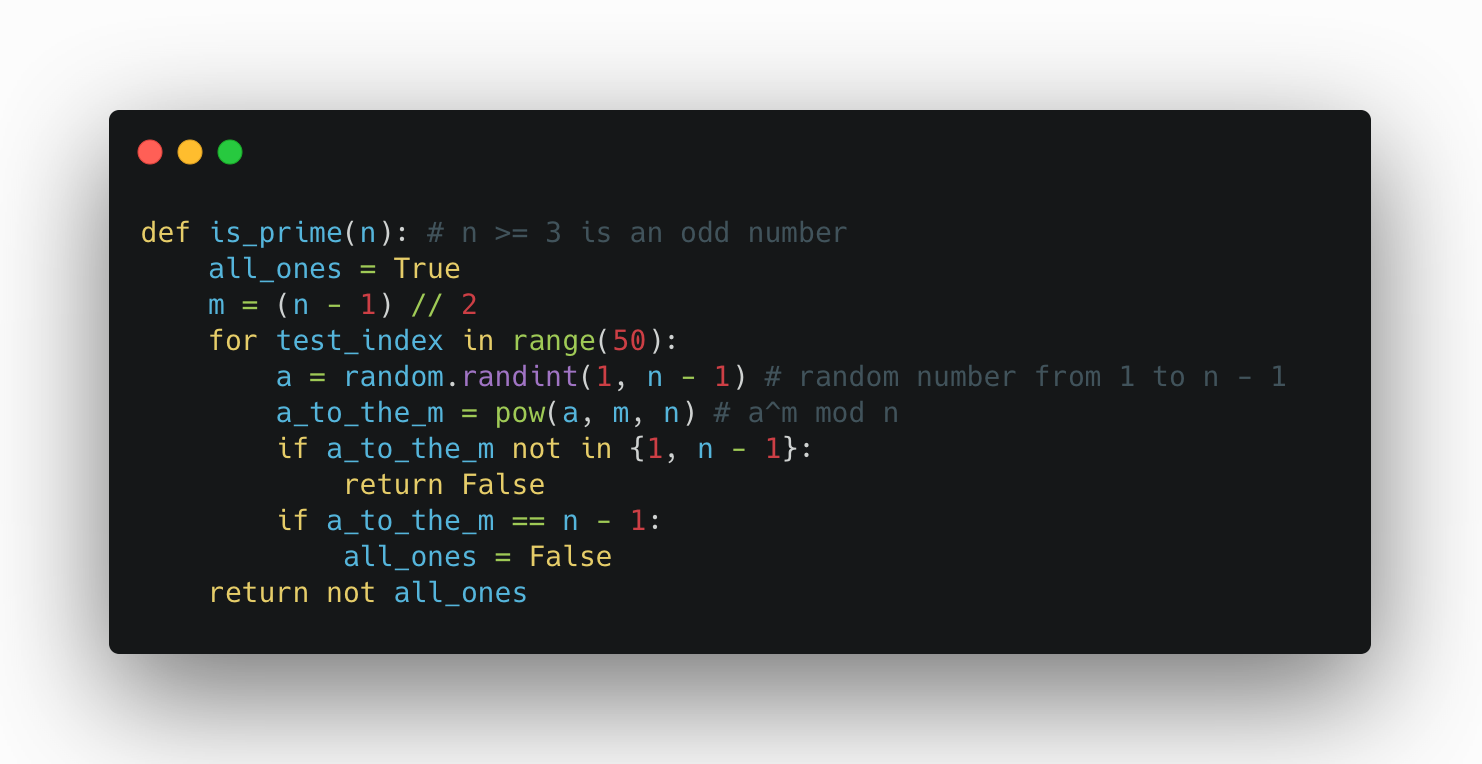
Мы запускаем 50 раз что-то похожее на тест Ферма, но вместо проверки, что a^(n-1) дает остаток 1, мы проверяем, что a^((n-1)/2) дает остаток 1 или -1. А также в конце мы делаем еще одну маленькую проверку: если все 50 раз a^((n-1)/2) давало остаток именно 1, то мы говорим, что число не простое. Вероятность ошибки этого алгоритма не больше 1/2^50.

Почему же этот алгоритм работает? Я попытаюсь не использовать теорию групп в рассуждениях, чтобы вы могли понять доказательство даже если знакомы только с теорией чисел.

Для начала докажем, что если n действительно простое, то алгоритм вернет False с вероятностью 1/2^50. Это всегда верно, что a^((n-1)/2) дает остаток 1 или -1. При этом ровно половина a-шек даст остаток 1, и половина даст остаток -1. Поэтому вероятность того, что все они были равны единице, составляет 1/2^50.

Теперь перейдем к доказательству в более сложную сторону: если n — составное, то алгоритм вернет True с вероятностью не больше 1/2^50.

Предположим, что в принципе существует такое a, что a^((n-1)/2) сравнимо с по модулю n с x, не равным ±1. Тогда по аналогии с тестом Ферма мы докажем, что таких a должно быть не меньше половины от всех, а значит, мы не встретим ни одного из них с вероятностью не больше 1/2^50.

Почему же это так? Посмотрим на значения a^((n-1)/2) для всех a от 1 до n-1. Все остатки разбиваются на группы одинаковых размеров (k), дающие одинаковый остаток при возведении в степень (n-1)/2. При этом мы точно знаем, что хотя бы в одной группе значение не равно ±1. Из этого мы уже можем понять, что таких чисел хотя бы одна треть от всех, потому что остатки ±1 есть у не более 2k элементов. Однако на самом деле их не меньше половины. Если из остатков ±1 есть только один, то хороших остатков ровно k, а плохих, как мы знаем, не меньше k. Если же есть и остаток 1, и остаток -1, то посмотрим на остаток b, такой что b^((n-1)/2) дает остаток -1. Тогда (ab)^((n-1)/2) дает остаток -x, который не может быть равен x, потому что n нечетно. Тогда у нас есть как минимум две группы плохих остатков, а значит, плохих остатков не меньше 2k, а хороших ровно 2k. Что и требовалось доказать.

Теперь предположим, что для всех a от 1 до n-1 число a^((n-1)/2) сравнимо с ±1 по модулю n. Это похоже на случай чисел Кармайкла для теста Ферма, однако для нашего теста данный вариант ничего не ломает. Нам надо доказать, что если мы всегда получаем остатки ±1, то тогда мы на самом деле всегда получаем именно остаток 1, и тест точно провалится на последней проверке.

Сперва предположим, что n — это степень простого, то есть n=p^k, где k>1. Мы знаем, что для всех остатков a^((n-1)/2) сравнимо с ±1 по модулю n. Тогда a^(n-1) всегда сравнимо с 1. При этом по модулю степени простого всегда существует первообразный корень b. То есть минимальная степень, в которой b дает остаток 1, — это phi(n)=(p-1)*p^(k-1). При этом мы знаем, что b^(n-1) тоже дает остаток 1, Тогда n-1=p^k-1 должно делиться на phi(n). Но первое не делится на p, а второе делится. Противоречие.

Теперь пускай n не является степенью простого. Тогда n можно представить как произведение двух взаимно простых чисел x и y, больших единицы. Пускай есть остаток a, для которого a^((n-1)/2) сравнимо с -1 по модулю n. Тогда в частности a^((n-1)/2) сравнимо с -1 по модулю x. По китайской теореме об остатках, так как x и y взаимно просты, существует такой (единственный) остаток b по модулю n, что b сравнимо с a по модулю x и b сравнимо с 1 по модулю y. Тогда b^((n-1)/2) сравнимо с a^((n-1)/2) (то есть с -1) по модулю x, а также b^((n-1)/2) сравнимо с 1 по модулю y. Но ведь если бы b^((n-1)/2) было сравнимо с ±1 по модулю n, то остатки по модулям x и y должны были бы быть либо оба 1, либо оба -1. Противоречие.

Таким образом, мы доказали, что в случае, если по модулю n в степени (n-1)/2 есть что-то кроме ±1, то таких остатков не меньше половины (и тест вернет неверный результат с вероятностью не больше 1/2^50), а если есть только ±1, то на самом деле есть только 1 (и тест всегда вернет верный результат).

Обратите внимание, что это редкий алгоритм, в котором бывают и ложноположительные, и ложноотрицательные результаты.

На практике этот тест работает примерно так же быстро, как и тест Миллера — Рабина.

По аналогии с тестом Миллера — Рабина вместо случайных чисел можно брать числа по порядку из-за гипотезы Римана.