Private Information

🛑 ALL INFORMATION CLICK HERE 👈🏻👈🏻👈🏻
Private Information
From Wikipedia, the free encyclopedia
^ Baumeler, Ämin; Broadbent, Anne (17 April 2014). "Quantum Private Information Retrieval has Linear Communication Complexity". Journal of Cryptology . 28 : 161–175. arXiv : 1304.5490 . doi : 10.1007/s00145-014-9180-2 .
^ Jump up to: a b Chor, Benny; Kushilevitz, Eyal; Goldreich, Oded; Sudan, Madhu (1 November 1998). "Private information retrieval" (PDF) . Journal of the ACM . 45 (6): 965–981. CiteSeerX 10.1.1.51.3663 . doi : 10.1145/293347.293350 .
^ Jump up to: a b c Kushilevitz, Eyal; Ostrovsky, Rafail (1997). "Replication is not needed: single database, computationally-private information retrieval". Proceedings of the 38th Annual Symposium on Foundations of Computer Science . Miami Beach, Florida, USA: IEEE Computer Society. pp. 364–373. CiteSeerX 10.1.1.56.2667 . doi : 10.1109/SFCS.1997.646125 . ISBN 978-0-8186-8197-4 .
^ Cachin, Christian; Micali, Silvio; Stadler, Markus (1999). "Computationally Private Information Retrieval with Polylogarithmic Communication". Advances in Cryptology - EUROCRYPT '99 . Prague, Czech Republic: Springer-Verlag. pp. 402–414. doi : 10.1007/3-540-48910-X_28 . ISBN 978-3-540-48910-8 .
^ Jump up to: a b Lipmaa, Helger (2005). "An Oblivious Transfer Protocol with Log-Squared Communication". Proceedings of the 8th International Conference on Information Security (ISC 2005) . Lecture Notes in Computer Science. 3650 . Singapore: Springer-Verlag. pp. 314–328. CiteSeerX 10.1.1.73.8768 . doi : 10.1007/11556992_23 . ISBN 978-3-540-31930-6 .
^ Gentry, Craig; Ramzan, Zulfikar (2005). "Single-Database Private Information Retrieval with Constant Communication Rate". ICALP . LNCS. 3580 . Springer. pp. 803–815. CiteSeerX 10.1.1.113.6572 . doi : 10.1007/11523468_65 .
^ Kiayias, Aggelos; Leonardos, Nikos; Lipmaa, Helger; Pavlyk, Kateryna; Tang, Qiang (2015). "Optimal Rate Private Information Retrieval from Homomorphic Encryption". Proceedings on Privacy Enhancing Technologies 2015 . 2015 . DE GRUYTER. pp. 222–243. doi : 10.1515/popets-2015-0016 .
^ Jump up to: a b Lipmaa, Helger (2010). "First CPIR Protocol with Data-Dependent Computation". Proceedings of the 12th International Conference on Information Security and Cryptology . Lecture Notes in Computer Science. 5984 . Seoul, Korea: Springer-Verlag. pp. 193–210. CiteSeerX 10.1.1.215.7768 . doi : 10.1007/978-3-642-14423-3_14 . ISBN 978-3-642-14423-3 .
^ Ishai, Yuval; Kushilevitz, Eyal; Ostrovsky, Rafail; Sahai, Amit (2004). "Batch codes and their applications" (PDF) . STOC'04 . ACM. pp. 262–271. doi : 10.1145/1007352.1007396 . Retrieved 2015-10-23 .
^ Ostrovsky, Rafail; Skeith III; William E. (2007). "A Survey of Single-Database Private Information Retrieval: Techniques and Applications". Proceedings of the 10th International Conference on Practice and Theory in Public-Key Cryptography . Springer-Verlag. pp. 393–411. doi : 10.1007/978-3-540-71677-8_26 . ISBN 978-3-540-71677-8 .
^ Jump up to: a b Percy++ / PIR in C++ at SourceForge
^ Di Crescenzo, Giovanni; Malkin, Tal; Ostrovsky, Rafail (2000). "Single Database Private Information Retrieval Implies Oblivious Transfer". Eurocrypt 2000 . LNCS. 1807 . Springer. pp. 122–138. doi : 10.1007/3-540-45539-6_10 .
^ Ishai, Yuval; Kushilevitz, Eyal; Ostrovsky, Rafail (2005). "Sufficient Conditions for Collision-Resistant Hashing". Proceedings of the Second Theory of Cryptography Conference . Cambridge, MA, USA: Springer-Verlag. pp. 445–456. doi : 10.1007/978-3-540-30576-7_24 . ISBN 978-3-540-30576-7 .
^ Jump up to: a b Saint-Jean, Felipe (2005). "A Java Implementation of a Single-Database Computationally Symmetric Private Information Retrieval (cSPIR) protocol" (PDF) . Yale University Technical Report YALEU/DCS/TR-1333 .
^ "Popcorn" (PDF) . Archived from the original (PDF) on 2016-08-21 . Retrieved 2016-05-26 .
^ "encryptogroup/RAID-PIR" . GitHub . Retrieved 2016-05-26 .
^ "SealPIR" . Github . Retrieved 2018-06-07 .
^ "upPIR" . uppir.poly.edu . Archived from the original on 2016-06-25 . Retrieved 2016-05-26 .
^ "XPIR-team/XPIR" . GitHub . Retrieved 2016-05-26 .
A. Beimel, Y. Ishai, E. Kushilevitz, and J.-F. Raymond. Breaking the
O
(
n
1
/
(
2
k
−
1
)
)
{\displaystyle O(n^{1/(2k-1)})}
barrier for information-theoretic private information retrieval. Proceedings of the 43rd Annual IEEE Symposium on Foundations of Computer Science , Vancouver, Canada, pages 261-270, 2002.
A. Beimel and Y. Stahl, Robust information-theoretic private information retrieval , in Proceedings of the 3rd International Conference on Security in Communication Networks (SCN'02), pp. 326–341, 2003. Cite is from DGH 2012, op. cit.
[DGH 2012] Casey Devet, Ian Goldberg , and Nadia Heninger , Optimally Robust Private Information Retrieval , 21st USENIX Security Symposium, August 2012.
[AG 2007] C. Aguilar-Melchor and P. Gaborit. A lattice-based computationally-efficient private information retrieval protocol , Western European Workshop on Research in Cryptology (WEWoRC), 2007.
[CGKS 1998] B. Chor, O. Goldreich, E. Kushilevitz, and M. Sudan, Private information retrieval , Journal of the ACM, 45(6):965–981, 1998.
[Goldberg 2007] I. Goldberg, Improving the robustness of private information retrieval , IEEE Symposium on Security and Privacy (S&P), 2007.
[HOG 2011] R. Henry, F. Olumofin, and I. Goldberg, Practical PIR for electronic commerce , ACM Conference on Computer and Communications Security (CCS), 2011.
[LG 2015] W. Lueks and I. Goldberg, Sublinear scaling for multi-client private information retrieval , International Conference on Financial Cryptography and Data Security (FC), 2015.
[DHS 2014] D. Demmler, A. Herzberg, and T. Schneider, RAID-PIR: Practical multi-server PIR , In Cloud computing security workshop (CCSW), 2014.
[ABFK 2014] C. Aguilar-Melchor, J. Barrier, L. Fousse, and M.-O. Killijian, "XPIR: Private Information Retrieval for Everyone", Cryptology ePrint Archive, Report 2014/1025, 2014.
[GCMSAW 2016] T. Gupta, N. Crooks, W. Mulhern, S. Setty, L. Alvisi, and M. Walfish, [1] Scalable and private media consumption with Popcorn. USENIX NSDI, March 2016.
[Cappos 2013] J. Cappos, Avoiding theoretical optimality to efficiently and privately retrieve security updates , International Conference on Financial Cryptography and Data Security (FC), 2013.
Sergey Yekhanin. New locally decodable codes and private information retrieval schemes, ECCC TR06-127 , 2006.
[ACLS 2018] S. Angel, H. Chen, K. Laine, S. Setty, PIR with compressed queries and amortized query processing , IEEE Symposium on Security and Privacy (S&P), 2018.
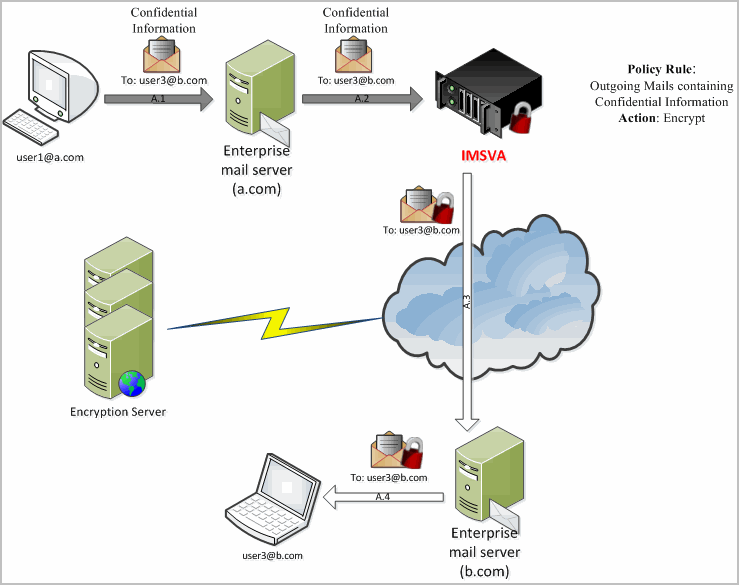
In cryptography , a private information retrieval (PIR) protocol is a protocol that allows a user to retrieve an item from a server in possession of a database without revealing which item is retrieved. PIR is a weaker version of 1-out-of- n oblivious transfer , where it is also required that the user should not get information about other database items.
One trivial, but very inefficient way to achieve PIR is for the server to send an entire copy of the database to the user. In fact, this is the only possible protocol (in the classical or the quantum setting [1] ) that gives the user information theoretic privacy for their query in a single-server setting. [2] There are two ways to address this problem: make the server computationally bounded or assume that there are multiple non-cooperating servers, each having a copy of the database.
The problem was introduced in 1995 by Chor, Goldreich, Kushilevitz and Sudan [2] in the information-theoretic setting and in 1997 by Kushilevitz and Ostrovsky in the computational setting. [3] Since then, very efficient solutions have been discovered. Single database (computationally private) PIR can be achieved with constant (amortized) communication and k-database (information theoretic) PIR can be done with
n
O
(
log
log
k
k
log
k
)
{\displaystyle n^{O\left({\frac {\log \log k}{k\log k}}\right)}}
communication.
The first single-database computational PIR scheme to achieve communication complexity less than
n
{\displaystyle n}
was created in 1997 by Kushilevitz and Ostrovsky [3] and achieved communication complexity of
n
ϵ
{\displaystyle n^{\epsilon }}
for any
ϵ
{\displaystyle \epsilon }
, where
n
{\displaystyle n}
is the number of bits in the database. The security of their scheme was based on the well-studied Quadratic residuosity problem . In 1999, Christian Cachin, Silvio Micali and Markus Stadler [4] achieved poly-logarithmic communication complexity. The security of their system is based on the Phi-hiding assumption . In 2004, Helger Lipmaa [5] achieved log-squared communication complexity
O
(
ℓ
log
n
+
k
log
2
n
)
{\displaystyle O(\ell \log n+k\log ^{2}n)}
, where
ℓ
{\displaystyle \ell }
is the length of the strings and
k
{\displaystyle k}
is the security parameter. The security of his system reduces to the semantic security of a length-flexible additively homomorphic cryptosystem like the Damgård–Jurik cryptosystem . In 2005 Craig Gentry and Zulfikar Ramzan [6] achieved log-squared communication complexity which retrieves log-square (consecutive) bits of the database. The security of their scheme is also based on a variant of the Phi-hiding assumption. The communication rate was finally brought down to
1
{\displaystyle 1}
by Aggelos Kiayias , Nikos Leonardos , Helger Lipmaa , Kateryna Pavlyk , Qiang Tang , in 2015. [7]
All previous sublinear-communication computational PIR protocol required linear computational complexity of
Ω
(
n
)
{\displaystyle \Omega (n)}
public-key operations. In 2009, Helger Lipmaa [8] designed a computational PIR protocol with communication complexity
O
(
ℓ
log
n
+
k
log
2
n
)
{\displaystyle O(\ell \log n+k\log ^{2}n)}
and worst-case computation of
O
(
n
/
log
n
)
{\displaystyle O(n/\log n)}
public-key operations. Amortization techniques that retrieve non-consecutive bits have been considered by Yuval Ishai , Eyal Kushilevitz , Rafail Ostrovsky and Amit Sahai . [9]
As shown by Ostrovsky and Skeith, [10] the schemes by Kushilevitz and Ostrovsky [3] and Lipmaa [5] use similar ideas based on homomorphic encryption . The Kushilevitz and Ostrovsky protocol is based on the Goldwasser–Micali cryptosystem while the protocol by Lipmaa is based on the Damgård–Jurik cryptosystem .
Achieving information theoretic security requires the assumption that there are multiple non-cooperating servers, each having a copy of the database. Without this assumption, any information-theoretically secure PIR protocol requires an amount of communication that is at least the size of the database n . Multi-server PIR protocols tolerant of non-responsive or malicious/colluding servers are called robust or Byzantine robust respectively. These issues were first considered by Beimel and Stahl (2002). An ℓ-server system that can operate where only k of the servers respond, ν of the servers respond incorrectly, and which can withstand up to t colluding servers without revealing the client's query is called " t -private ν-Byzantine robust k -out-of-ℓ PIR" [DGH 2012]. In 2012, C. Devet, I. Goldberg, and N. Heninger (DGH 2012) proposed an optimally robust scheme that is Byzantine-robust to
ν
<
k
−
t
−
1
{\displaystyle \nu Homemade Group Porn
Oral Cum Porn
Kinky Mature
Trans Nasty
Pics Naked Free