Принцип Парето та самоподібність

Летючка

Почнемо з питання:

Якщо топ 20% агентів володіє 80% ресурсів, то скількома відсотками ресурсів володіє топ 1% агентів?

Умова -- це твердження принципу Парето. Агентами можуть бути будь-хто, а ресурсами -- будь-що. В оригінальному спостереженні Парето агентами були італійські землевласники. Звичайно, що в різних сферах числа будуть різними, проте до кожної ситуації намагаються підібрати формулювання так, аби числа у твердженні в сумі давали сотню, хоч вони і не є сумовними -- з суто мнемонічних міркувань. То що там про золотий відсоток?

Здавалось би, умова неповна, але я вас прошу -- коли це ви не залишали решту припущень в умові як вправу для читача? Робота науківця -- сформулювати гіпотезу, навести припущення, отримати результат, і вже тоді в розділі Обговорення розкритикувати реальність за невідповідність припущенням. Привіт, гітарасти, давно не бачились, як і з СУПЕРСИМЕТРИЧНИМИ ПАРТНЕРАМИ (перепрошую за кросовер).

Яка задача, такі й припущення, тому припустимо, що серед топ 20 % агентів присутня точно така ж нерівність, як і у всьому світі, тобто цій задачі. Тоді топ 20% з цих топ 20% агентів володітимуть 80% від 80% ресурсів, себто топ 4% володітимуть 64%. Аналогічно, .8% володітимуть 51.2%. А отже, у власності золотого відсотка знаходиться більше, ніж половина всіх ресурсів. Ось так і живемо.

Виглядає як софістика

Чи валідне це припущення? Насправді, воно є значно реалістичнішим, ніж однорідний розподіл серед кожної з груп агентів. І цікавішим, звичайно. Я знаходжу некоректним, але провокуючим спосіб мислити про це за допомогою результатів цього дослідження на лабораторних щурах, проведеного в 1993. Там щурів індивідуально навчили здобувати їжу пірнаючи під воду. Потім поділили на одностатеві групи по 6 щурів і почали спостерігати протягом кількох тижнів. Як виявилось, половина щурів у групі (ледарі) жодного разу не пірнала у басейн, натомість крадучи їжу у тих, хто пірнав (годувальники). Цей розподіл на ледарів та годувальників утворився за перші 25% від всієї тривалості експерименту, протягом яких відбувались як бійки за їжу, так і більшість невдалих спроб вкрасти її один у одного. Проте цікавішим був другий етап експерименту, де утворили окремі групи суто з ледарів та суто годувальників відповідно, теж одностатеві. Як виявилось, групи знову поділились навпіл, і колишні годувальники могли запросто змінити статус, як і ледарі. А могли й не змінити. Тобто роль визначалась виключно середовищем, а не особистими якостями.

Так і серед середнього класу є нерівний розподіл на багатших та бідніших, як і серед багатіїв та навіть бідних. І взагалі у довільній групі, пригадайте довільний населений пункт, від мегаполісу та смт до міста та села. Це явище називається самоподібністю, коли частини чи підгрупи цілого відображають таку ж поведінку. Його можна спостерігати і у самоврядуванні, яке, незалежно від рівня (країна, місто, громада, університет, факультет, катедра) має схожу ієрархічну структуру та три гілки влади. Часто самоподібність (або ж масштабна інваріантність) виникає у самоорганізовуваних системах, як от люди, біологічні мікроагенти, фінансові ринки абощо. Тому спокійно можна очікувати її виникнення і серед розподілу ресурсів. З цього і випливає валідність припущення.

Аналітичний підхід

Проте чи згодна з цим математика? І як взагалі виглядатиме функція такого розподілу? Для початку, поглянемо як обраховуються величини, про які говориться в загадці. Топ-х % агентів визначається через впорядкування всіх агентів за розміром ресурсів у їхній власності, і тоді додаванням до групи усіх, починаючи з найбагатшого, так, аби розмір групи становив х% від розміру популяції агентів -- очевидно. Аналітично це виглядає так: якщо нам дана густина розподілу f(x), себто багатствами у розмірі від х до х+dx володіє f(x)dx відсоток населення, то у-відсотиль, ака у-квантиль, або ж у-персентиль, визначатиметься з наступного рівняння:

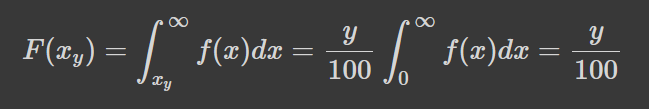
Де F(x) це кумулятивна функція розподілу, а x_y -- у-квантиль, або ж найменше значення х у топ-y%, як от мінімальний розмір статків серед групи олігархів. Верхньою межею служить максимально можливий розмір статків, що, звичайно, залежить від статків і не обов'язково є нескінченним. Аналогічно мінімумом необов'язково є нуль, особливо за допустимості явища заборгованості. Також ми використали умову повноти, а саме, що інтеграл густини розподілу по всьому проміжку рівний одиниці. Остаточно зазначимо, що ми означили квантиль та кумулятивну функцію трохи не так, як їх означають зазвичай. Зазвичай відсотки рахуються знизу, а тому наше x_y відповідатиме 100-y квантилю у класичному сенсі. Аналогічно, кумулятивну функцію F(x), яка рахує частку популяції, що має багатство більше за x, ми обраховуємо згори, а не знизу, тому F(0)=1, а F(oo)=0.

Розмір же статків у у-квантилі визначатиметься з наступного рівняння:

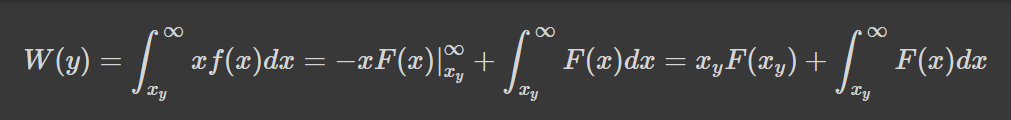
Де я здійснив абсолютно необов'язкове, проте бажане інтегрування частинами після другого знаку рівності. Також у останній формулі я припустив, що F(x) спадатиме до нуля швидше, ніж 1/x, інакше загальні статки популяції були б рівні безкінечності, і поняття "80% ресурсів" не мало б сенсу. Тепер, маючи все необхідне, запишемо рівняння, якому має задовольняти наша функція за умовою:

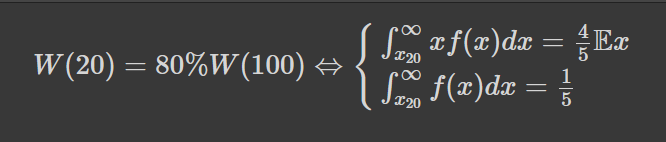
Де ми використали, що W(100) відповідає всім багатствам (багатство топ-100%, себто всіх агентів), а також тотожності цього виразу до означення матсподівання. Зазначимо, що W(y) лише пропорційно до розміру статків людства, і його потрібно домножити на розмір популяції аби отримати абсолютний розмір. Проте у наших формулах розмір популяції агентів скорочується. Якщо ж вам не зрозуміло, чому ця величина пропорційна до розміру статків, то замініть у виразі Nf(x)dx на m(x), де N -- розмір популяції, а m(x) -- відповідно кількість людей, які володіють статками від x до x + dx гривень, і все стане на свої місця.

Можна побачити, що наведене рівняння задовольняють дуже багато функцій. Тому почнемо з припущення, що правило 80 на 20 застосовне до довільного топ відсотку агентів, а отже для як завгодно малого теж. Тоді, рівняння внизу мають виконуватись для всіх 0<y<1 (ми віднормували y до 1 замість 100, у %):

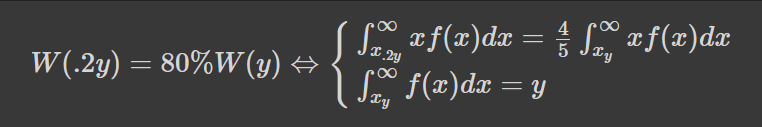
Для простоти вважатимемо, що максимальне багатство у популяції таки обмежене певним m. Розглянемо його окіл, а саме проміжок [m-z,m] з малим z. Можна показати, що в такому випадку обидва рівняння суперечитимуть одне одному, якщо тільки f(m) не рівне нулю або безкінечності. Що очікувано. Тому ми підемо іншим шляхом -- візьмемо похідну по у:

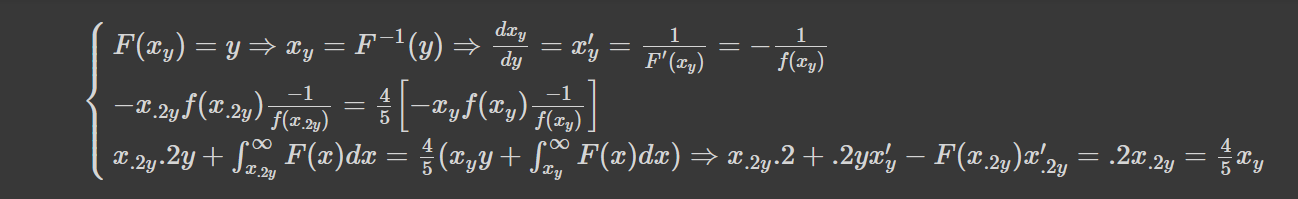
В першому рядку ми знайшли похідну від x_y і використали цей результат у другому рядку при знаходженні похідної від інтегралу, залежного від параметру. Третій рядок це альтернативний запис рівності у другому рядку. Приходимо до співвідношення:

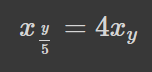
Тобто топ-20%у квартиль є вчетверо більшим за топ-у квартиль. Чи дає нам це щось нове? Чи могли ми записати цю рівність одразу? Не виглядає так, що могли б. Зауважимо, що аби правило виконувалось для як завгодно малих квартилів, необхідно аби максимальний статок був необмеженим, як видно з рівності при підстановці у=0 і як було показано раніше. Також мінімальний можливий статок має бути більше нуля для виконання правила для всього розподілу (у=1). В реальності все зазвичай навпаки -- обмеження згори є, а знизу -- нуль, якщо тільки кожен громадянин не отримує непередаровний до самої смерті клапоть землі і два раба.

Властивості

Маючи лише останню формулу на руках, можна отримати багато цікавих властивостей розподілу. Вже зрозуміло, що частина розподілу, починаючи з довільного х, виглядатиме точно так само, як і весь розподіл. Спробуємо тепер інтерпретувати формулу кількісно і подивимось на наслідки.

Тож, якщо мінімальна дозволена кількість ресурсів це 1 умовна одиниця (у.о.), то багатії з більше, ніж 4 у.о. на руках володіють 80% всіх наявних багатств, або ж у них вчетверо більше ресурсів, ніж у агентів з 1-4 у.о. Запишемо це так: 4:=4(1_4). У багатіїв з 8 у.о. і більше на руках вчетверо більше ресурсів, ніж у люду з 2-8 у.о.: (8:=4(2_8)). Тоді за допомогою простого віднімання можна побачити, що у категорії 4-8 у.о. (4:-8:=4_8) вчетверо більше ресурсів, ніж у 1-2 у.о. мінус 4-8 у.о. (1_4-2_8=1_2+2_4-2_4-4_8=1_2-4_8), себто 4-8 у.о. має на 20% менше, ніж 1-2 у.о. (4_8=4(1_2-4_8) -> 5(4_8)=4(1_2)). Аналогічно, 3-12 у.о. має вчетверо менше, ніж 12+ у.о., а отже 1-3 у.о. без 4-12 у.о. мають вчетверо менше, ніж 4-12 у.о., що призводить до 4(1_3)=5(4_12). Аналогічна арифметика дає 4(2_3)=5(8_12), тобто в загальному можна показати, що 4(a_b)=5(4a_4b). Аби з'єднати відрізки, покладемо b=4a, і отримаємо 4(a_4a)=5(4a_16a).

Як це інтерпретувати згідно з принципом Парето? Повернемось на початок і пригадаємо, що категорія 4: містить в собі 20% популяції, тому 1_4 це 80%. Також у групі 2_8 вчетверо більше агентів, ніж у 8:, і тепер правила можна записати як 1_4=4(4:), відповідна решта перетворень набуде вигляду 4(4_8)=1_2-4_8 -> 5(4_8)=1_2 -> a_b=5(4a_4b) -> a_4a=5(4a_16a). Тобто з лівого краю розподілу ми бачимо, що вп'ятеро місткіша група має лише на 25% більше багатств, тобто 83.(3)% найбідніших агентів володіють 55.(5)% багатств. Не так вже й нерівно, мусимо зазначити. Шкода достатньо лише змінити знак аби побачити, що серед бідних 44.(4)% багатств належать 16.(6)% найбагатших бідних, що вже не виглядає так надихаюче.

Як щодо відрізку, який знаходиться посеред розподілу? Можемо сказати, що останнє правило застосовне до довільного відрізку у розподілі, який закінчується вшістнадцятеро далі від нуля, ніж починається: топ 16.(6)% володіють 44.(4)% багатств. Схожі ігри призведуть і до інших співвідношень, але ми краще просто скористаємось аналітичною формулою.

Вигляд розподілу

Відповідь вже відома -- розподіл Парето, або ж звичайний степеневий розподіл, який є значно поширенішим у реальному світі, ніж нормальний гаусівський. Він має наступну кумулятивну функцію та густину розподілу:

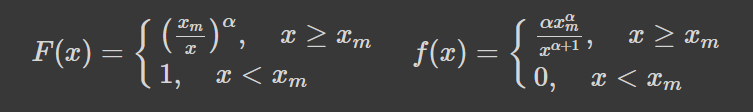
Поглянемо, як співвідносяться частки популяцій на відрізках [ka,kb] та [kc,kd], де k -- певна безрозмірна стала, від 0 і аж до безкінечності:

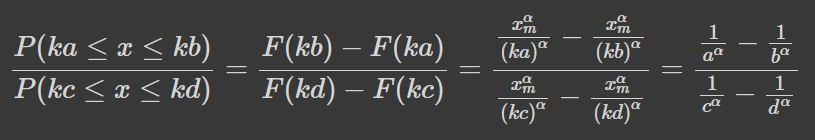
Це відношення є незалежним від k! Тобто степеневий розподіл володіє самоподібністю. Для прикладу: якби достаток був розподілений за Парето, і люди з доходом від 8 тис до 12 тис у. о. всумі володіли б вчетверо більшою кількістю грошей, ніж люди з доходом від 2.5 тис до 6 тис, то аналогічно люди з доходом 8-12 млн володіють вчетверо більшою кількістю грошей, ніж люди з доходом 2.5-6 млн. Тобто багатства бідних, середнього класу, мільйонерів, та олігархів будуть розподілені в певному однаково в межах своїх груп.

Результат не зміниться, якщо обрізати розподіл згори певним x_c -- з'явиться лише нормувальний множник до кумулятивної функції та функції розподілу, який скоротиться у вищенаведеному обчисленні.

Перевіримо виконання принципу Парето:

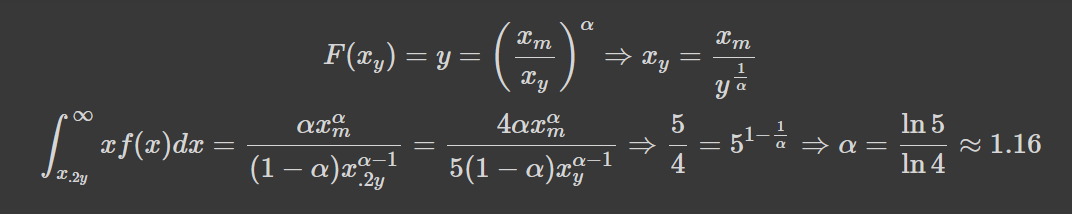
Виконується для показника ~1.16. Єдине завдання, яке лишається -- змусити розподіл працювати на відрізку [0,x_c], який є значно поширенішим. Цього можна досягти заміною змінних, наприклад:

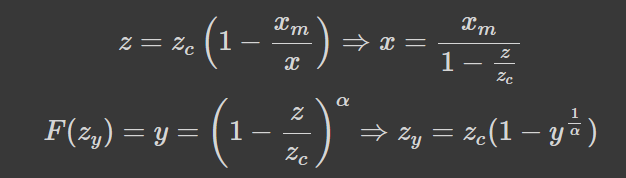
Це дозволяє зберегти самоподібність, проте принцип Парето більше не виконується для всіх y. Для y=1 можна отримати:

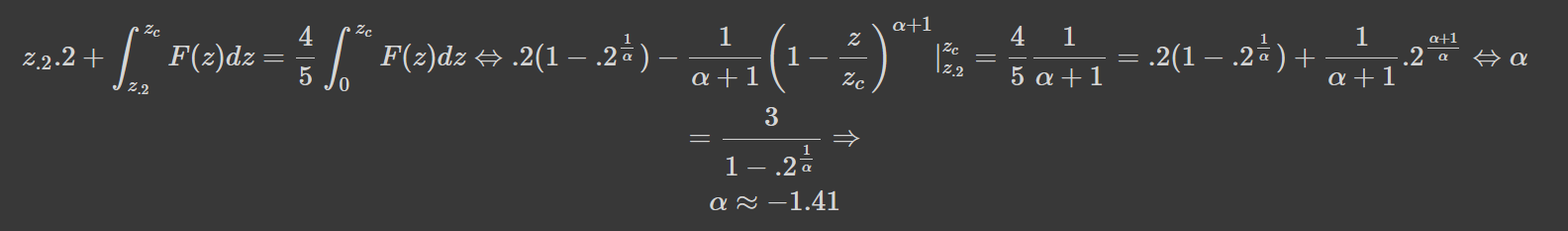
Як бачимо, досягти виконання принципу Парето для обмеженої величини неможливо, бо від'ємний показник не лізе ні в які ворота (це означає, що ймовірність мати певний статок зростає з його розміром).

Поглянемо, чи можна користуватись ним наближено до певного x_с. Пригадаймо, що 20% квартиль вчетверо більший за мінімум. Тоді 4% квартиль вшістнадцятеро більший, .8% квартиль -- в 64 рази, і так далі. Для обрізання на .032% квартилю, що відповідатиме нехтуванню 32 агентами у 100 тис. популяції, максимум рівний 1024-ом мінімумам. Тобто на проміжках між певним значенням і вищим за нього на три порядки розподіл може працювати.

Ще один з варіянтів вирішення проблеми може критись в розширенні розподілу Парето до IV типу:

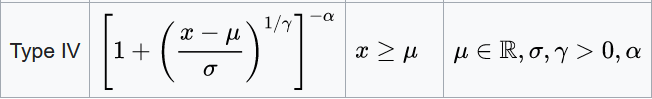
Але мені вже лінь займатись такою математикою. Наостанок зазначимо, що дискретна версія розподілу Парето зветься розподілом Зіфа-Мандельброта, і є застосовнішою за свій неперервний аналог у зв'язку з частою дискретністю розглядуваної величини.

Застосування

Тисячі їх. Ледь не все у світі розподілено за степеневим розподілом, від поширеності слів у мові (Зіф був лінгвістом) та росту акцій за день до довжин річок, розмірів, популярності творів, та ін. Складно знайти поширеніший розподіл, ніж цей. До речі, розмір файлів на вашому комп'ютері теж має цей розподіл, тому не варто нехтувати дріб'язковим сміттям, бо накопичується воно в гору не легшу, ніж один фільм в full HD.

Ще моя улюблена властивість -- для показника менше або рівного 1 розподіл не має середнього, а при менше або рівне 2 -- стандартного відхилення. У інших же випадках ці числа не кажуть про розподіл абсолютно нічого. Числа, які як ми вже вивчили, є часом безглуздими, але єдиними крихтами знань для типових користувачів статистики, і тому спостерігати як ті отримують беззмістовні значення при їхньому обрахунку -- сама насолода.

По ідеї, розподіл виникає всюди, де є якась самоорганізація. Також його люблять системи в околі фазових переходів.

Остання сигарета

Наостанок, задамося питанням:

Чи буде в середньому для вибірки з розподілу з правильним альфа виконуватись правило 80% на 20%?

Встановимо це емпірично:

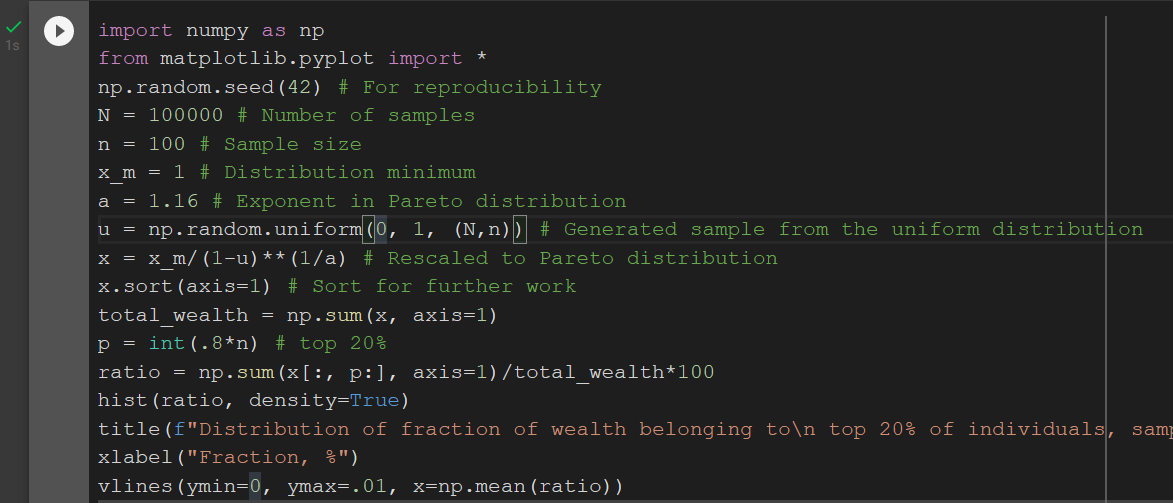
На рисунках далі чорна лінія позначає середнє. Як видно, частка ресурсів в руках топ 20% агентів схоже має логнормальний розподіл (нормальний по логарифму величини) з середнім, яке наближається до 80% зі збільшенням вибірки, проте дуже повільно.

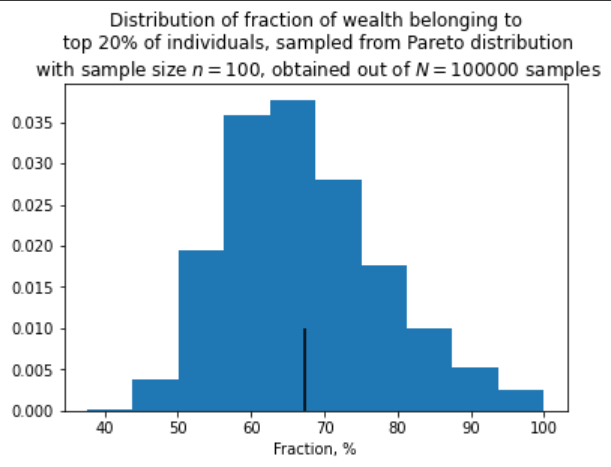
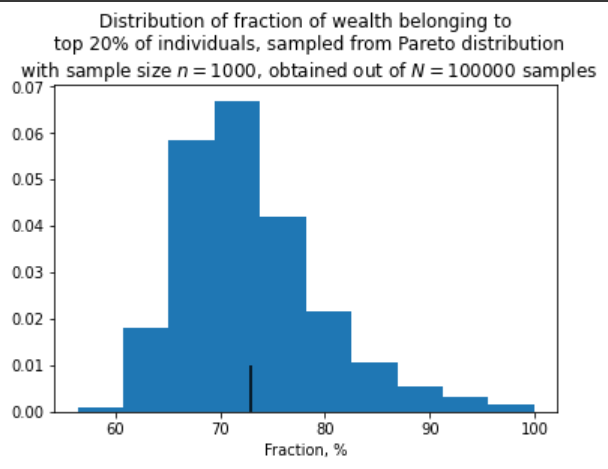
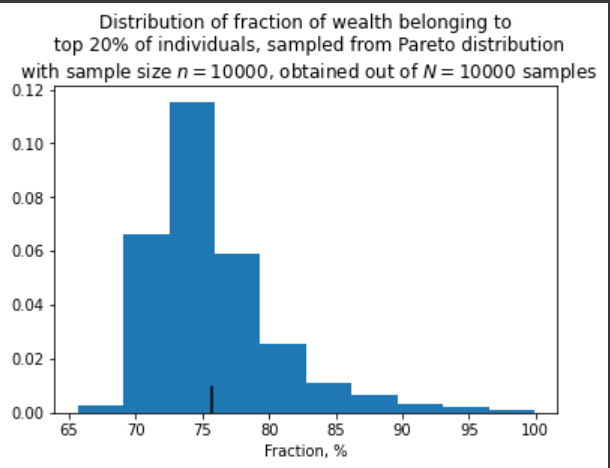
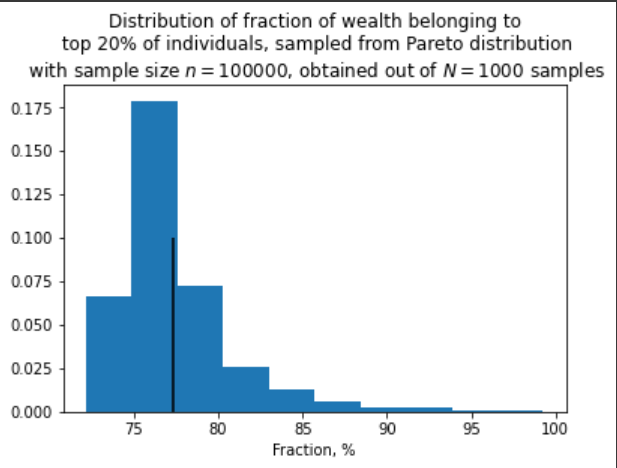
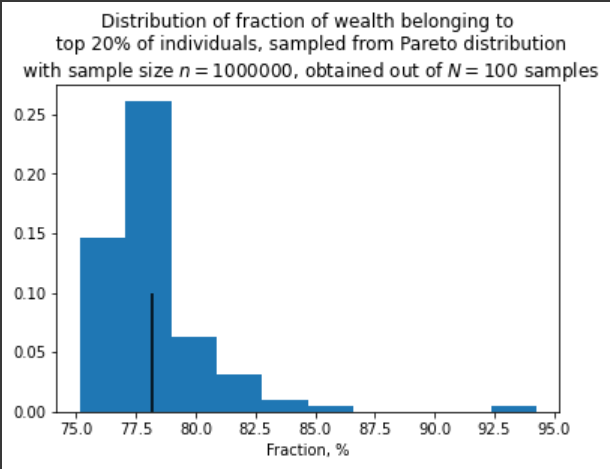
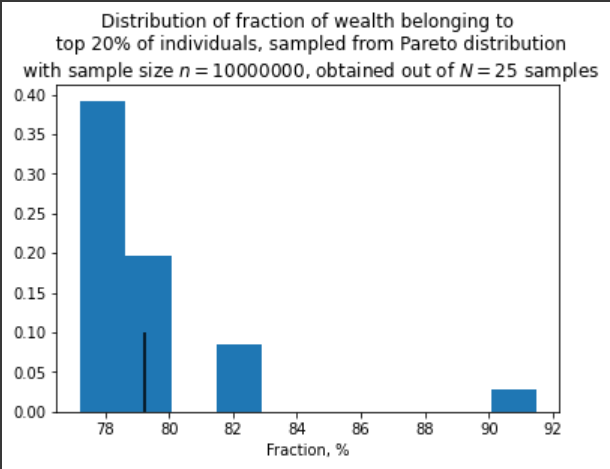
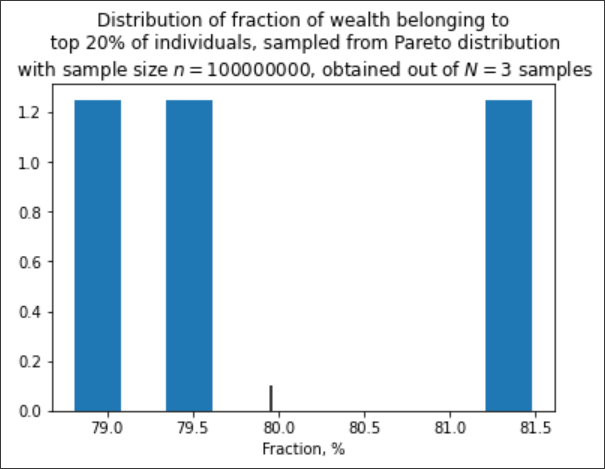
І остання картинка:

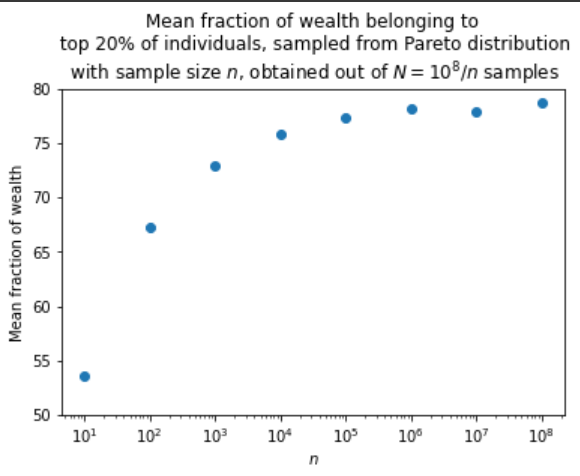
Ви, до речі, помітили, що навіть при великих n розподіл не наближається до нормального? Це тому, що розподіл Парето з таким показником має безкінечну дисперсію, і тому до нього центральна гранична теорема незастосовна. З цієї ж причини до середнього дуже повільне сходження. Коли матиму знання, можливо напишу про властивості таких розподілів та extreme value theory, а поки що вистачить.