Применение Bayesian подхода в A/B тестах
Evgeny - @evga85Я очень увлечен оптимизацией процессов, и классический вариант проведения A/B тестов меня не устраивал долгое время. Ощущение что все, или почти все продакты просто приняли способ обработки теста как так должно быть и не ищут новых путей. Есть калькулятор A/B теста, и на том хорошо.
- Я хочу уменьшить как можно сильнее количество “испытуемых”, т.к. хочу влиять на продуктовый опыт как можно меньшего количества людей.
- Нехватка пользователей во многих проектах тормозит получение результата и соответственно количество самих экспериментов.
- Даже если достаточно пользователей, то сократить их количество в тесте до самого возможного минимума, при этом сохранив статзначимость результата. Как минимум это позволит проводить больше отдельных тестов.
Ну и нужно наконец ввести обратно в моду здравый смысл, а не повсеместный расчет там где нужно и нет, слепо следуя инструкциям и формулам. И это моя попытка найти золотую середину.
Еще проблема в классическом подходе, то что подчинение правилу расчета количества выборки заранее и установление ожидаемого эффекта катастрофически замедляет эксперимент.
Конечно установление количества выборки заранее помогает избежать ошибки в традиционном подходе, НО чтоб определить количество выборки вы должны установить минимальный заметный эффект, или ожидаемую конверсию и т.д. Но ведь если вы установите этот эффект неверно, это сильно повлияет на последствия вашего теста и главное скорость.
Для определение небольшого эффекта требуется огромное количество пользователей для стат.значимости.
Установив большой ожидаемый эффект вы рискуете не заметить или точнее не принять во внимание небольшое, но тоже положительное изменение. Очень много продкутологов проводят эксперименты потому что они не знают что может случиться, соответственно определение каких-то желаемых результатов заранее не имеет никакого смысла вообще.
Теперь к делу.
Я начал проводить эксперименты на своих же экспериментах.
А именно, использовал Bayesian подход для фиксирования решения при проведении теста ранее чем заканчивался ход эксперимента по классическому пути расчета доверительного интервала. То есть в определенный момент(об этом ниже) я записал результат, но продолжил ход эксперимента чтоб посмотреть какой будет результат по стандартному пути. Либо при такой же длительности эксперимента брал в расчет в 2 раза меньше пользователей. Такое соотношение взял из этой статьи, где ребята это рассчитали.
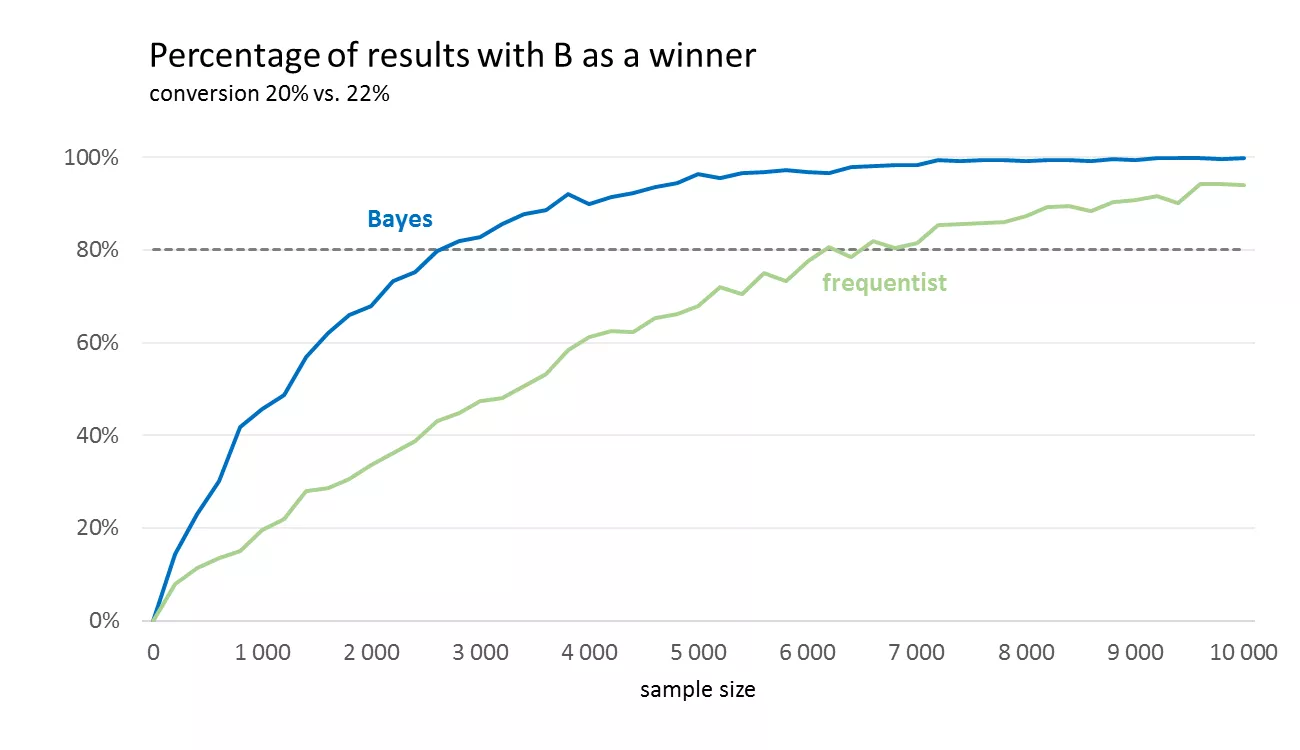
На данный момент я сравнил 10 экспериментов. Каждый длился по 2 недели, и все 10 показали, что если бы я раньше закончил эксперимент согласно Bayesian подходу, или взял бы меньшее количество пользователей в том же периоде, то мое решение после тестирования было бы таким же что и при стандартном подходе. Вряд ли это случайность. Но даже если случайность, в примере ниже я опишу почему этого можно не бояться или принять.
В общем, это первый несомненный плюс.
Но так же большим преимуществом Bayesian подхода является наличие в расчетах результата вероятности ошибки и ее величины.
Стандартный Chi-Squared test при p-value 0,05 нам дает информацию что есть лишь 5% вероятности что полученный результат это случайность, и минимум 95% вероятности что результат не случаен. Но никто не знает что будет если вдруг это случайность.
А я хочу определять значимый результат как только он появляется при проведении теста, и без предопреденения заранее минимального заметного эффекта и не ждать пока в тесте достигается заданный размер выборки, который опять же рассчитывается заранее, что заведомо ограничивает результат теста.
Как оказалось этим вопросом задаюсь не только я, но почему то пока больше в англоязычных источниках. Русскоязычные продакты этой проблемой пока не особо заинтересованы.
Bayesian же подход в случае если мы ошибочно примем новую гипотезу (то есть вариант B, а он окажется хуже) помимо доверительного интервала еще дает значение насколько будет хуже, а так же процентную вероятность что B лучше A.
Например, 10% вероятность что вариант B хуже, и это повлечет собой ухудшение конверсии на 0,09%. Соответсвенно 90% шансов что В лучше.
Прелесть этого в том, что я могу рассчитать чем грозит принятие и внедрение варианта B и соотношение успеха и провала. Даже не просто рассчитать, а принять заранее риск. То есть величину ухудшения, наш риск, например, на 0,1% я определяю заранее, предопределяя свои потери. И теперь самое важное, я останавливаю тест при достижении этого значения ухудшения, менее 0,1% пункта.
Здесь калькулятор Bayesian A/B test for conversion
https://vidogreg.shinyapps.io/bayes-conversion-test/
Допустим, у нас была конверсия 5%, а вариант B показал конверсию 6%.
В случае ошибки конверсия уменьшится на 0.089% то есть станет 4.91%.
Так же рассчитано что B лучше чем A с вероятностью 83.6%.
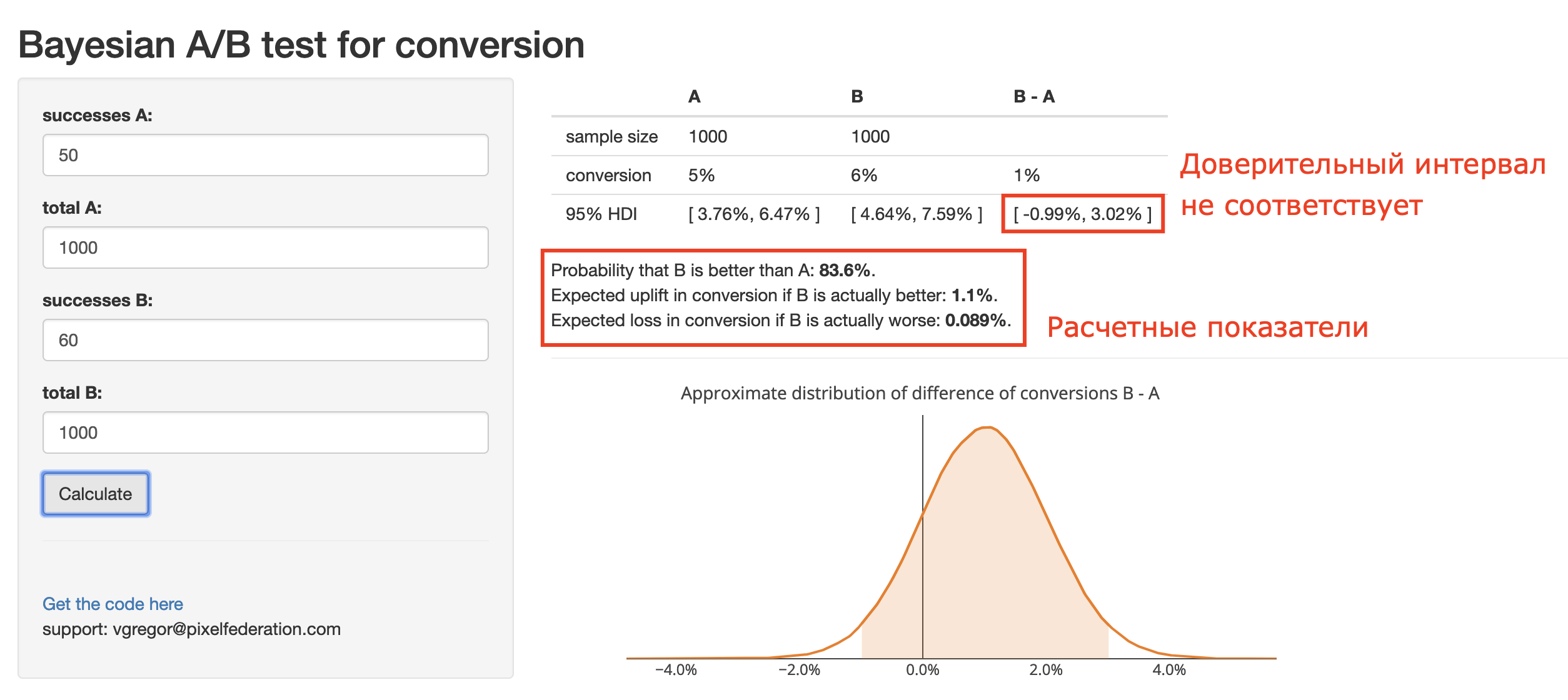
Мы приняли вариант B в результате эксперимента, т.к. ухудшение меньше предопределенного нами риска 0,1%.
Отсюда можно в деньгах, или в пользователях, или в % посчитать цену ошибки, в зависимости от вашей целевой метрики. Но как я говорил выше, я ее уже определил, просто сейчас мы ее сравниваем с получившейся новой конверсией при положительном результате.

Можно рассматривать это как ставку, мы готовы пожертвовать Х количеством денег (если гипотеза НЕверна), с возможностью заработать 10Х (если верна). И вот тут важно соотношение, оно и позволит принимать решение.
У нас есть данные, что приблизительно с 84% вероятностью вы заработаете 10Х, а с 16% вероятностью потеряете 1Х. Таким образом соотношение еще выше.
1 к 5 в вероятности верности гипотезы, и 1 к 10 в потерях/доходах.
В отличие от стандартного подхода мы здесь знаем наши предполагаемые потери и принимаем их, а там есть лишь вероятность верности гипотезы более 95%, а что если это ошибка?
Суть не в том что данные здесь менее статистически значимы, это в принципе другой вариант не только расчета, а подхода к принятию решения.
Таким образом решение принимаем быстрее и обходимся малой кровью. Можно заняться новым экспериментом, тем самым обработав большее количество гипотез. Конечно, это грубый пример, просто чтоб показать принцип применения.
Ну и наверное это совершенно неважно для крупных компаний кто может себе позволить выставить порог значимости 99,9%. Я такого позволить себе не могу, как и многие другие.
PS.
Ремарка. Я далеко не академический специалист в статистике, и это лишь моя попытка оптимизации процесса проведения тестов т.к. стандартный подход меня не устраивает.
Если вы находите это все неверным, или наоборот полезным, то welcome пишите мне @evga85, буду рад обменяться опытом.
При изучении данной темы использовал эти ресурсы:
https://mobiledevmemo.com/its-time-to-abandon-a-b-testing/
http://varianceexplained.org/r/bayesian-ab-testing/
Тут хорошо описано само математическое обоснование этого подхода
https://cdn2.hubspot.net/hubfs/310840/VWO_SmartStats_technical_whitepaper.pdf
http://www.indiana.edu/~kruschke/BEST/BEST.pdf
https://www.evanmiller.org/ab-testing/t-test.html
И др.