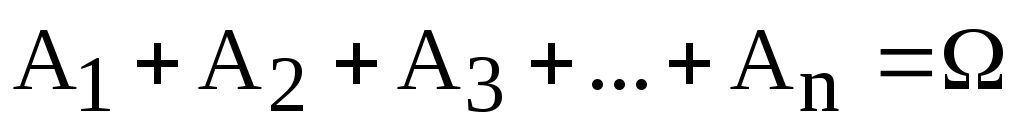Правила сложения вероятностей
https://t.me/data_analysis_ml
Аксиома: Вероятность суммы или наступления хотя бы одного из двухнесовместных событийравна сумме вероятностей этих событий (аддитивность Р):
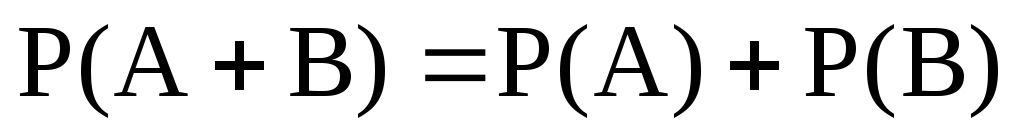
Данную аксиому иногда называют «теоремой сложения», так как для опытов, сводящихся к «схеме случаев», она может быть доказана.
Эта аксиома легко обращается на любое число несовместных событий: вероятность суммы несовместных событий равна сумме вероятностей этих событий:
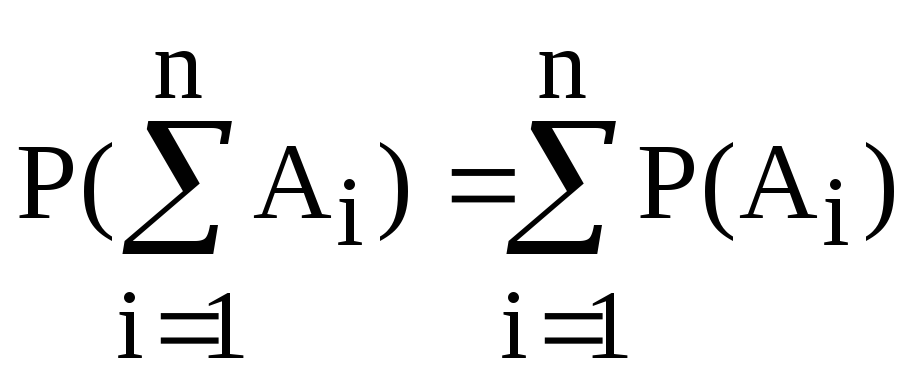
Пример 1: Вероятность попадания в башню танка при одном выстреле – 0,2, в его корпус – 0,1, в ходовую часть – 0,025. Найти вероятность попадания в танк при одном выстреле.
Решение:
Обозначим интересующее нас событие через А = {попадание в танк}, тогда А1= {попадание в башню танка}, А2= {попадание в корпус танка}, А3= {попадание в ходовую часть}.
Очевидно, что попадание в танк наступит тогда, когда снаряд попадет либо в башню, либо в корпус, либо в ходовую часть танка. Таким образом, интересующее нас событие А будет являться суммой событий А1; А2; А3:

А так как события А1; А2; А3несовместные (наступление одного из них исключает появление другого), то вероятность наступления события А определится как:
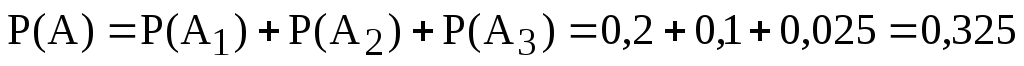
Вывод: Полученный результат означает, что при проведении достаточно большого числа стрельб в аналогичных условиях в среднем в 325 стрельбах из 1000 будет получено попадание в танк.
Из данной аксиомы вытекают два важных следствия.
Следствие 1. Если события А1, А2, …Аnобразуют полную группу несовместных событий (
), то сумма их вероятностей равна единице.
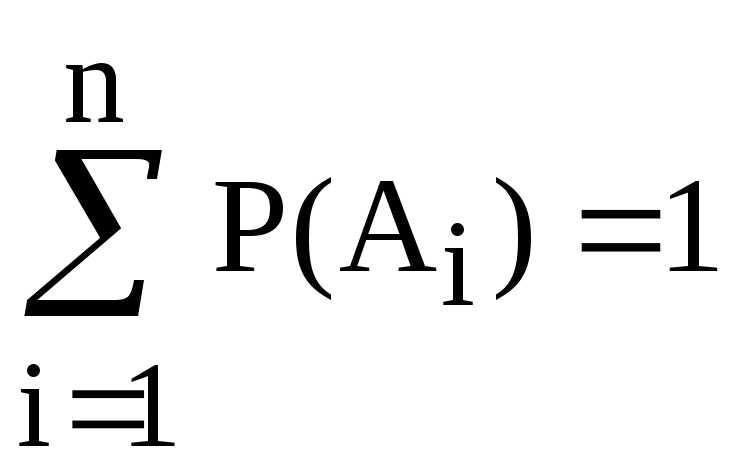
Следствие 2.Сумма вероятностей противоположных событий равна 1.
Р(А) + Р(
) = 1
Для совместных событийаксиома примет следующий вид:
Вероятность суммы, или наступление хотя бы одного из двух совместных событий, равна сумме вероятности этих событий без вероятности произведения этих событий:
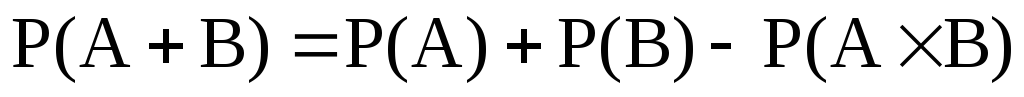
Справедливость этого тождества наглядно следует из его геометрической интерпретации (рис. 1).



АВ

АК
А









В
В

Ω
Ω
а б
Рис. 1
На диаграмме Эйлера-Венна вероятность наступления событий А (или В) по существу есть площадь области, при попадании случайной точки в которую, наступает событие А (или В). Тогда вероятность комбинации А + В будет соответствовать площади заштрихованной области (рис. 1.а). Чтобы получить такую же по площади область, необходимо из площади областей наступления событий А и В вычесть площадь их совместного появления АВ (рис. 1.б).
Пример 2: Вероятность подавления батареи противника из-за потерь только в личном составе составляет 0,15, вследствие повреждения материальной части - 0,45, а из-за потерь одновременно в личном составе и материальной части - 0,25. Какова вероятность подавления артиллерийской батареи?
Решение:
Пусть событие А = {подавление личного состава батареи}, а событие В = {повреждения материальной части}. Тогда одновременное подавление личного состава и повреждение материальной части будут являться совместным наступлением событий А и В или АВ.
Вероятность наступления события А по условию задачи равна 0,15 (Р(А)=0,15), вероятность наступления события В равна 0,15 (Р(В)=0,45), вероятность совместного наступления события А и В равна 0,25 (Р(АВ)=0,25).
Требуется найти вероятность события С ={подавления батареи противника}, которое будет заключаться либо в подавлении личного состава батареи, либо в повреждении материальной части либо того и другого, или Р(А+В).
Применив теорему сложения вероятностей, получим:
Р(С) = Р(А + В) = Р(А) + Р(В) – Р(АВ) = 0,15 + 0,45 - 0,25 = 0,35.
Вывод:Полученный результат означает, что при проведении достаточно большого числа стрельб в аналогичных условиях в среднем в 35 стрельбах из 100 батарея противника будет подавлено, т.е. поражен либо личный состав, либо повреждена техника, либо и то и другое.