Последовательность Колакоски
Последовательность Колакоски получила своё название в соответствии с принципом Арнольда: "Никакое научное открытие не было названо в честь первооткрывателя".
На самом же деле её обнаружил американский математик и инженер Руфус Ольденбургер. Он изучал самогенерирующиеся последовательности и доказал:
Существует и единственна последовательность из двух символов, кодирующая собственную последовательность длин серий:
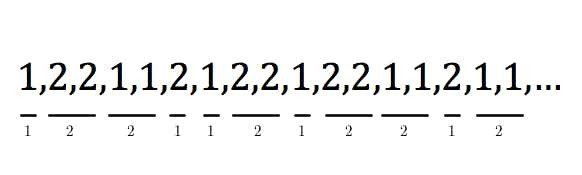
В заумном определении кроется очень простая закономерность. Если посчитать сколько раз подряд в последовательности повторяются одинаковые символы, то получится сама последовательность. Подобное свойство наделяет последовательность самоподобием или фрактальностью. Кроме того, последовательность является бесконечной и апериодической, то есть никогда не повторяет себя.
Ольденбургер работал в этой области в 1939 году. Может из-за того, что все научные силы того непростого времени были брошены на другие задачи, последовательность была забыта. И только в 1965 году закономерность всплыла снова, теперь уже в популярной математике. Уильям Колакоски опубликовал задачу про неё в American Mathematical Monthly, и она прославилась, получив имя совсем не того человека, который её обнаружил. В журнале задача шла под номером 5304:
Опишите простое правило для построения последовательности 1 2 2 1 1 2 1 2 2 1 2 2 1 1 2... Существует ли формула для n-го члена последовательности? Является ли последовательность периодической?
На оба вопроса задачи имеется ответ, и он отрицателен - это доказал ещё Ольденбургер. Но, в отличие от Ольденбургера, Колакоски рассматривал последовательность с началом, неограниченно она продолжалась только в одну сторону. При таком условии единственность, доказанная Ольденбургером для "двусторонних" последовательностей, нарушается.
Эдмунд Харрис в своей книге умудрился талантливо визуализировать этот ряд чисел:
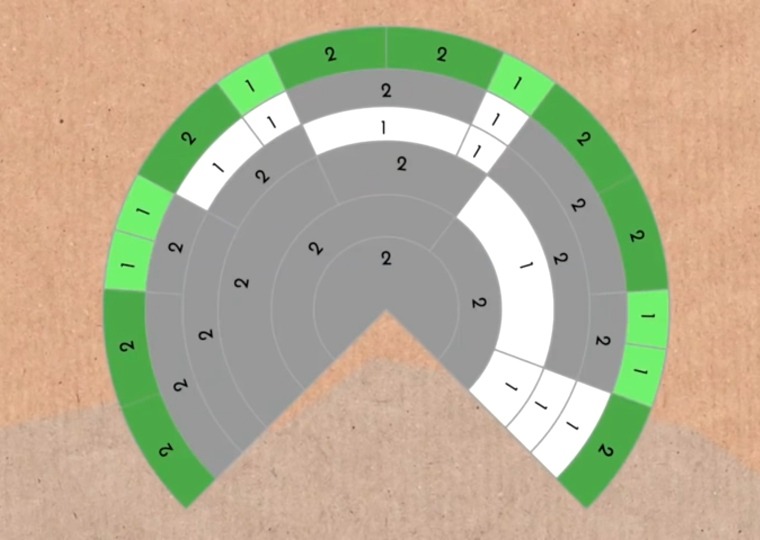
Последовательность начинается с внешней окружности, а каждая последующая внутренняя описывает длины серий внешней. Если окрасить единицы и двойки разными цветами и стереть сами числа, получится интересный рисунок:
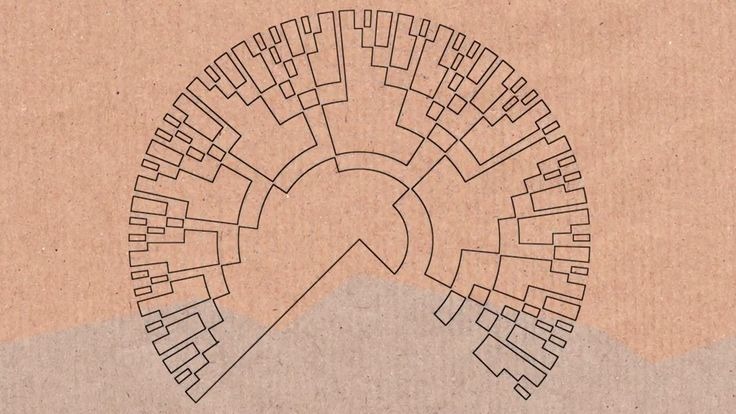
Присмотревшись, можно заметить повторяющийся фрактальный узор. По мере уменьшения колец узор углубляется и сдвигается.
Последовательность Колакоски ставит ряд интересных вопросов. На один из них ответ до сих пор не известен: каких чисел в последовательности больше, единиц или двоек? Выглядит так, будто соотношение приближается к 50/50 в пределе. Это одна из нерешённых математических проблем. Почти как гипотеза Коллатца, только за её решение станешь не настолько знаменитым :)