Почему громче 0 dB уже не будет

Органы чувств у людей (и не только у людей) построены весьма интересным образом. С точки зрения эволюции выгодно иметь способность слышать очень тихие звуки. Например, писк малярийного комара под ухом, чтобы дать ему леща и не заразиться. Или тихий шорох какой-нибудь притаившейся в кустах паскуды, тоже чтобы дать леща.  

Но в то же время, хорошо бы, имея такую дикую чувствительность, не глохнуть каждый раз от ударов грома или еще каких-то громких звуков. Писк комара и раскат грома по абсолютным величинам - например, по звуковому давлению или по энергии - могут различаться в миллионы раз. И человеку нужно нормально воспринимать и то, и другое. 

Поэтому человечий слух имеет логарифмическую чувствительность. То есть, если человеку кажется, что звук усилился в два раза - энергия этого звука увеличилась в десятки, а то и сотни и тысячи раз.

Что такое логарифмическая шкала? 

Дисклеймер: дальнейший текст не содержит математической точности и является лишь грубым примером, просьба убрать математиков от экрана.

Два метра на 1 больше, чем один метр. Три метра на 1 больше, чем 2 метра. Четыре метра на 1 больше, чем... ну вы поняли. Это пример линейных единиц измерения. 

А есть такие единицы измерения, в которых каждое следующее значение в несколько раз увеличивает число. 

Пример: я придумал новую единицу измерения. Назову ее Степенной Попугай, или СП. 

Правило у этой единицы измерения такое: 

1 СП = 10^1 тугриков (10 в степени 1, то есть 10 умножить на себя 1 раз)

2 СП = 10^2 тугриков (10 в степени 2, то есть 10 умножить на себя 2 раза)

3 СП = 10^3 тугриков (10 в степени 3, то есть 10*10*10) 

...и так далее.

Например, у меня есть 3 степенных попугая. Тут ко мне подходит товарищ (зовут его, допустим, Толян) и отдает мне должок в количестве еще 1 степенного попугая. Итого, у меня стало 4 степенных попугая.

То есть, у меня было 3 СП, а стало 4 СП, на один больше. 

Но по моим же правилам, которые я написал выше, у меня было 10^3, то есть 1000 тугриков. А стало 10^4, то есть 10000 тугриков. 

Чуете? При изменении на 1 единицу логарифмической величины количество тугриков увеличилось аж в 10 раз - было 1к, а стало 10к.

То есть. Возвращаясь к примеру с метрами. Два метра на 1 больше, чем один метр. Три метра на 1 больше, чем два метра. 

Но при этом два степенных попугая в 10 раз больше, чем 1 степенной попугай. Три СП в десять раз больше, чем два СП. 

В этом отличие логарифмической шкалы от арифметической - каждое следующее значение не "на сколько-то" больше, а "во сколько-то" больше.

Тут мы приходим к следующей проблеме

В прошлом примере у меня было 3 СП, то есть 1000 тугриков. Толян отдал мне еще один, и у меня стало 4 СП (10к тугриков). Несложно посчитать, что Толян мне отдал (10000 - 1000) = 9000 тугриков. 

Потом Толян у меня (добрая я душа!) снова занял 1 СП. И когда он снова пришел возвращать мне долг, у меня на кармане было, допустим, 5 СП, или 100к тугриков. Толян отдал мне еще один, и у меня теперь стало 6 СП или 1000к тугриков. То есть, в этот раз Толян отдал мне (1000к-100к) = 900к тугриков.

"Неплохой наварчик!" - подумал я. 

"Вот паскуда!" - подумал Толян. 

Толяну не повезло. В обоих случаях он брал в долг 1 СП, но в первый раз ему нужно было вернуть только 9к тугриков, а во второй - аж 900к. 

Мировое сообщество солидарно с Толяном, поэтому логарифмические единицы измерений не используются для абсолютных значений - когда нужно обозначать конкретное значение, количество.

Но они отлично подходят там, где нужно показать, во сколько раз одно значение отличается от другого.

И звук, как вы уже догадались - именно тот случай.

Как звук сохраняется в компьютере

Теперь нам нужно сделать некоторое отступление. Давайте разберемся, как компьютер хранит звук. 

Компьютер отлично работает с числами. И совсем не умеет работать ни с чем другим. Про дискретизацию мы поговорим как-нибудь в другой раз, сегодня давайте просто примем как факт: компьютер делит звуковую волну на точки и сохраняет положение и громкость каждой точки. 

Причем, эти значения фиксированные. Мы не можем ставить точки в рандомных местах - памяти компьютера не хватит, чтобы все записать. Вместо этого мы говорим - на то, чтобы записать громкость каждой точки, я готов выделить столько-то бит, и не битом больше. 

Если говорить про эту картинку - на ней для записи громкости используется 4 бита памяти. С помощью 4 битов можно записать 16 различных значений. Вот они там слева и показаны.

Таким образом, весь диапазон громкости на картинке делится на 16 значений. И максимальная громкость, которую мы можем записать в данном случае - 1111 в двоичной системе. 

А если хотим еще громче? Следующее после 1111 число - это 10000. Но это уже 5 бит, а нам разрешено использовать только 4. 

Вывод: в цифровом мире при сохранении звука есть максимально-возможное значение громкости, которое невозможно превысить, потому что не хватит бит для записи.

Начинаем все склеивать. 

Итак, мы имеем следующие тезисы:

1) Громкость звука меняется в очень больших диапазонах, и у человека восприятие громкости логарифмическое.

Что из этого следует? Чтобы было удобно работать со звуком, его нужно измерять логарифмической величиной. 

Но есть проблемка!

2) Логарифмические величины не годятся для отображения абсолютных значений, однако отлично подходят, чтобы показать, во сколько раз одно значение отличается от другого. 

Хм, тогда мы могли бы показывать, во сколько раз громкость конкретного аудио фрагмента отличается от какого-то фиксированного значения, некого стандарта... Который был бы одним и тем же независимо от компьютера, от телефона, от формата. Нужно что-то фундаментальное, что-то ограниченное математически... 

Вот только где бы его взять?.. Так, погодите-ка! 

3) В цифровом мире есть порог громкости, некоторое значение, громче которого быть уже не может. 

Так вот же он - этот стандарт! Мы можем измерять абсолютно все дорожки, все аудиофайлы относительно него - и тогда пропорция между их громкостью будет сохраняться. 

Именно так и работает измерение громкости в децибелах. 

За 0 dB принимается максимальное значение громкости, которое можно записать в файле. И тогда, если звук тише этого максимального значения, то мы получаем отрицательное значение (например, -3 dB, -6 dB). 

И фактически, говоря "громкость баса -5 dB", мы не говорим "громкость баса - столько-то попугаев". Мы как бы говорим "громкость баса в столько-то раз меньше, чем максимальная громкость, которую мы можем записать в аудиофайл".

Теперь можно ответить на главный вопрос: почему громче 0 dB быть не может? 

Потому что 0 dB - это и так максимальная громкость, которая помещается в аудиофайл. А если делать еще громче, то начинается искажение звуковой волны: те точки, которые достигли "потолка", так и остаются на этом уровне. А те, которые еще не на максимуме, продолжают ползти вверх.

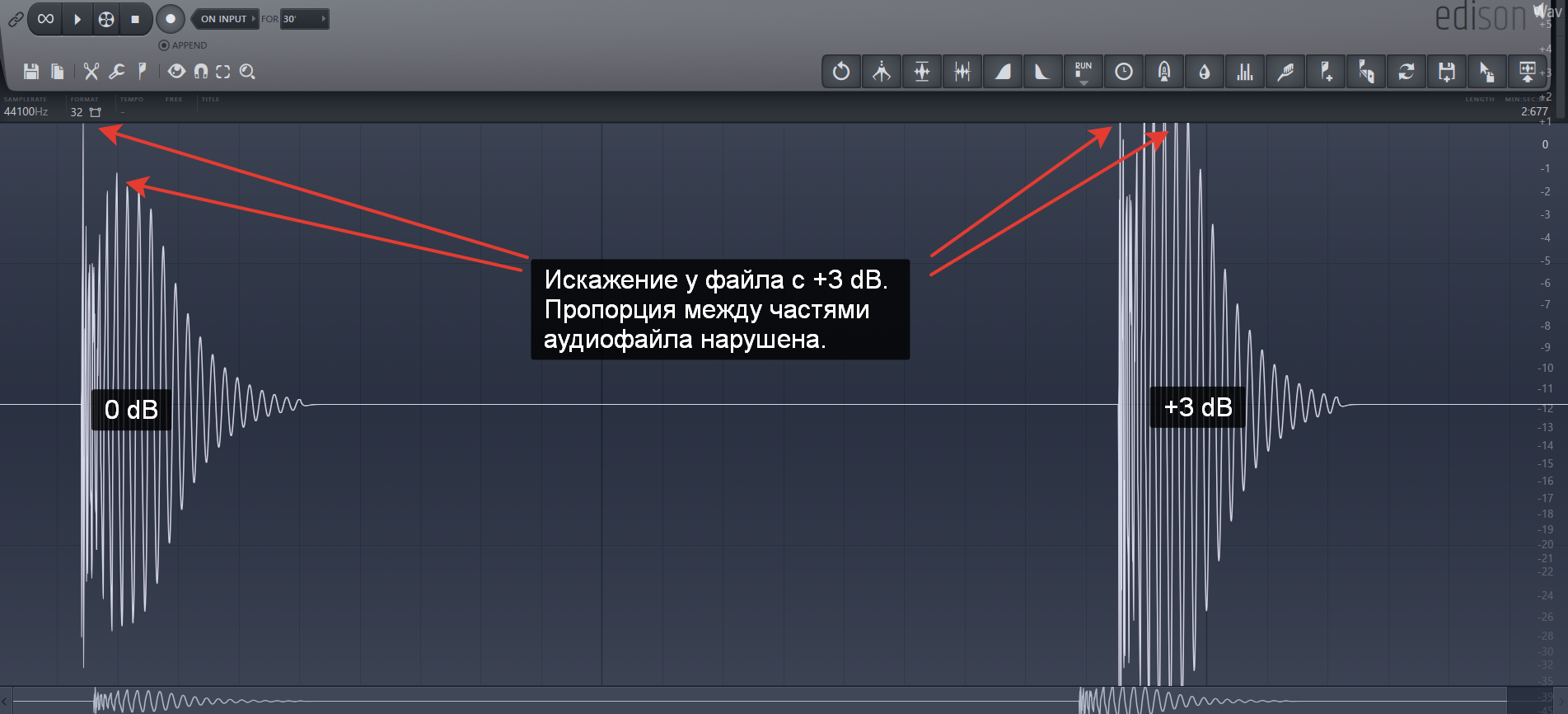
Название у этого явления - цифровое клиппирование. Его прекрасно видно на видео, которое я выше вставлял. 

То есть, хоть и на анализаторе уровня и может быть положительное значение в децибелах, фактически, это уже не истинная громкость волны, а скорее степень ее искажения.