Piękno równań opisujących liczbę π i trochę magii z okazji urodzin.
Nawet w starożytności ludzie zauważyli, że stosunek stosunek obwodu koła do długości jego średnicy jest zbliżony do trzech, lecz nie dokładnie trzech, tylko trochę więcej. W tamtych czasach taka postawa, nazwana później numerem 𝞹, nie wyróżniała się spośród wielu innych liczb, które można było określić eksperymentalnie.
Archimedes, będący prawdopodobnie pierwszym matematykiem badającym dokładniej własności liczby π w III w. p.n.e. oszacował ją z dokładnością do dwóch miejsc po przecinku. Użył do tego metody bazującej na zależnościach geometrycznych, metody pozwalającą oszacowywać π z (teoretycznie) dowolną dokładnością, przez następne wieki była metodą najlepszą, często niezależnie od prac Archimedesa wykorzystywaną przez późniejszych matematyków.
Jest całkiem prawdopodobne, że grecki matematyk był pierwszym, który dokładniej analizował właściwości liczby π. Obliczył on jej wartość na 22/7 (w związku z czym 22 lipca obchodzony jest Dzień Aproksymacji π), ograniczając dokładność do dwóch miejsc po przecinku. W swojej pracy wykorzystał geometrię.
Symbol π został pierwszy raz użyty w 1706 roku przez matematyka angielskiego Wiliama Jonesa. W powszechne użycie wszedł dopiero w połowie XVIII wieku po wydaniu Analizy L. Eulera.
Następnie matematycy zrozumieli, że liczba 𝞹 łączy objętość wielowymiarowej kuli i stopień jej promienia w przestrzeni o dowolnym wymiarze (z racjonalnym czynnikiem, który już zależy od wymiarów: dla 2 wymiarów jest to 1, dla 3 wymiarów - 4/3). Tak więc liczba 𝞹 nie zmieni się nawet dla naukowców mieszkających w przestrzeniach o różnej liczbie wymiarów niż nasza.
Jednak stosunek długości obwodu koła do jego średnicy zmienia się wraz ze zmianą krzywizny przestrzeni i pokrywa się z naszą stałą 𝞹 tylko w "płaskim" jednorodnym przypadku, tak aby ująć prościej w przestrzeni, dla których twierdzenie Pitagoras jest ważne. Jak twierdzi teoria względności, blisko horyzontu zdarzeń czarnej dziury przestrzeń jest silnie zakrzywiona. Więc możliwe, że cywilizacja, która miała szczęście pojawić się w takim miejscu, nie może podejrzewać istnienia stałej 𝞹.
Okazuje się, że liczba 𝞹 nagle pojawia się po prostu z naturalnego szeregu liczb. Angielski matematyk John Wallis, odkrył niesamowitą formułę zwaną wzorem Wallisa
Wzór Wallisa - rozwinięcie liczby π w iloczyn nieskończony uzyskany w roku 1655 przez Johna Wallisa. Historycznie wzór Wallisa był jednym z pierwszych przedstawień liczby π w postaci granicy ciągu liczb wymiernych, które było stosunkowo proste do wyliczenia. Wzór Wallisa ma postać:
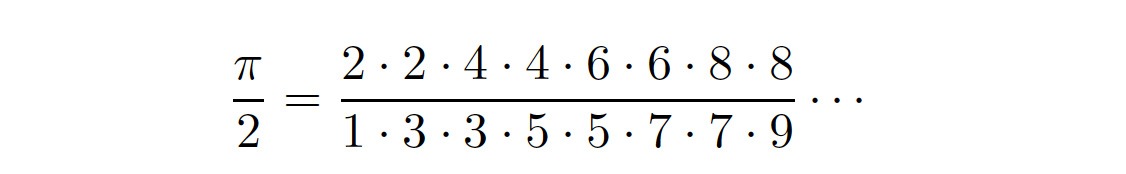
Jeszcze bardziej zaskakującą dla niewtajemniczonych jest formuła obejmująca liczbę 𝞹 uzyskana przez wielkiego matematyka Leonarda Eulera.
Wzór ten porównuje się z sonetami Szekspirowskimi i uważany jest za najpiękniejszy wzór matematyczny.
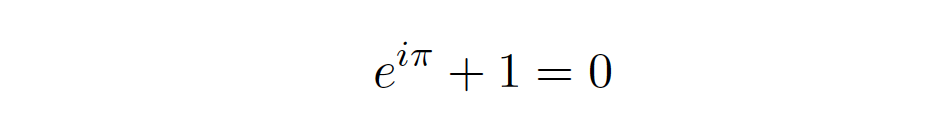
W powyższym równaniu wykorzystano trzy działania arytmetyczne: dodawanie, mnożenie i potęgowanie. Co więcej, zawiera ono pięć najważniejszych stałych matematycznych, użytych jednokrotnie: 0, 1, π, e, i.
0 – to najciekawsza liczba rzeczywista, element neutralny dodawania.
1 – Element neutralny mnożenia, w informatyce symbol prawdy.
π – liczba niewymierna, definiowana jako stosunek długości okręgu do długości średnicy tego okręgu, w przybliżeniu 3,1415.
e – podstawa logarytmu naturalnego w przybliżeniu wynosi 2,7182.
i – jednostka urojona liczby zespolonej.
W rzeczywistości wzór Eulera jest odpowiednikiem dwóch pięknych równań na raz:
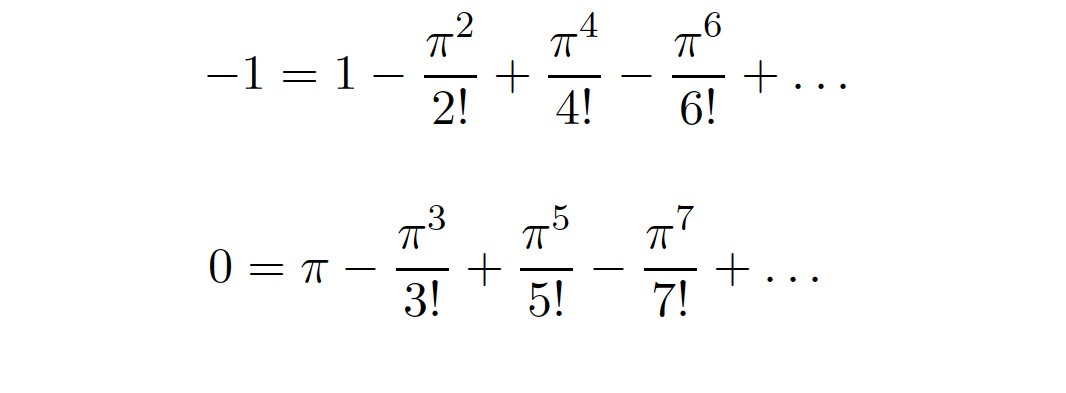
Chyba najważniejszą w historii liczby π, prawdziwie przełomową datą był rok 1882, w którym matematyk niemiecki F. Lindemann wykazał ostatecznie, że liczba π jest liczbą przestępną (to znaczy, że nie może ona być pierwiastkiem równania algebraicznego o współczynnikach całkowitych). Stąd wynika, że niemożliwa jest kwadratura koła.
Jego dowód był modyfikacją podanego przez Hermite'a dowodu przestępności liczby e.
Kolejna słynna formuła Eulera:

Ta formuła w odróżnianiu od powyższych bardziej nadaje się do przybliżonego obliczenia liczby 𝞹 I nawet jest bardziej odpowiednia do tego celu niż również ładna i ciekawa formuła wielkiego niemieckiego filozofa i matematyka Gottfrieda Leibniza:

Później okazało się, że formuła ta na długo przed tym, jak Leibniz ją opracował wyprowadził indyjski matematyk i astronom Madhawa z Sangamagramy.
Jego prace matematyczne zaginęły, ale są znane z późniejszych odwołań.
Madhawa podał m.in. wartość liczby pi z dokładnością do 11. miejsca po przecinku (3,14159265359).
Formuła Leibnitza jest właściwie szczególnym przypadkiem rozwinięcia w szereg Taylora funkcji arctan(x)
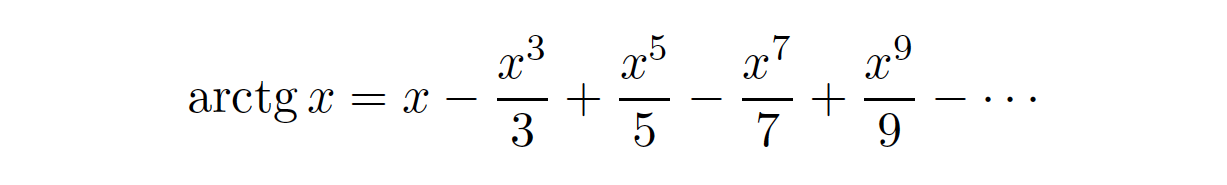
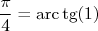
Przez długi czas, najwygodniejszym sposobem obliczania liczby 𝞹 było metoda angielskiego matematyka Johna Machina, który był sekretarzem Royal Society of Londyn, gdy był kierowany przez Newtona Izaaka.
Tak wygląda równianie Machina:
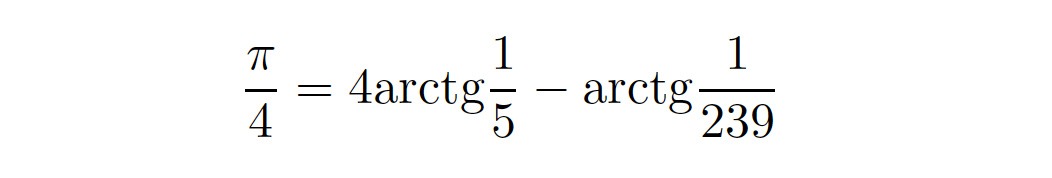
Liczba 𝞹 pojawia się w matematyce w najbardziej niespodziewanych miejscach. Na przykład matematyk Abraham de Mouvre (który uciekł do Anglii z Francji, gdzie był prześladowany jako hugenota) odkrył formułę znaną także jako całka Gaussa:
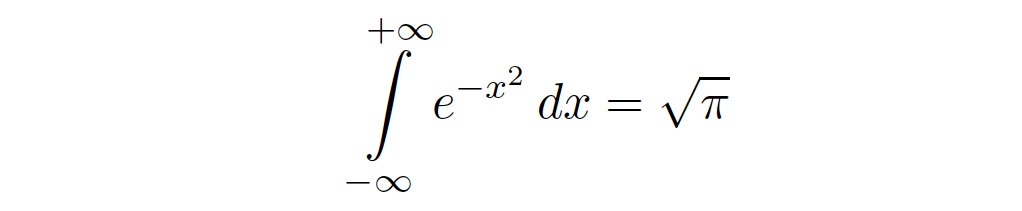
Mouvre, jak również inne wybitne matematycy Pierre-Simon de Laplace i Carl Friedrich Gauss udowodnili, że funkcja Φ(x) = e-x2/2/√2𝞹 to gęstość rozkładu normalnego, lub rozkładu Gaussa, który jest limitem dla arytmetycznej średniej ciągu niezależnych zmiennych losowych.
Całka ta ma szeroki zakres zastosowań. Przy niewielkiej zmianie zmiennych jest używana do obliczania normalizacji stałej rozkładu normalnego. Ta sama całka ze skończonymi granicami jest ściśle związania zarówno z funkcją błędu, jak i dystrybuantą rozkładu normalnego.
W fizyce tego typu całki pojawiają się często, np. w mechanice kwantowej, i są wykorzystywane do znajdowania gęstości prawdopodobieństwa stanu podstawowego oscylatora harmonicznego, również przy znajdowaniu propagatora dla oscylatora harmonicznego wykorzystujemy tę całkę.
Wydawałoby się, że tysiącletnia historia badań sugeruje, że nie przeoczyliśmy niczego ważnego w liczbie 𝞹 Jednak w 1997 r., ostatnio jak na skalę historyczną, była sensacja. Simon Plouffe znalazł nową prezentację dla liczby 𝞹 w formie ciągu:

Wzór Bailey-Borwein-Plouffe (wzór BBP) jest algorytmem spigota do obliczania n-ej cyfry binarnej stałej matematycznej π przy użyciu szesnastkowego systemu liczbowego. Za pomocą tego wzoru można bezpośrednio obliczyć wartość dowolnej podanej cyfry π bez obliczania poprzednich cyfr.
A teraz Mireczki ciekawosteki i trochę folii ( no a jak że bez tego :) )
Jak wyliczyli matematycy, użycie liczby π z 39 cyframi po przecinku pozwala na obliczenie obwodu obserwowalnego wszechświata z błędem mniejszym niż średnica atomu wodoru.
π jest znana z dokładnością 22 459 157 718 361 cyfr po przecinku – wartość ta została ustalona w listopadzie 2016 roku. Poświęcono na to 105 dni nieprzerwanej pracy wieloprocesorowego serwera.
Do dziś nie wiadomo, czy w ciągu cyfr, za pomocą których zapisane są przybliżenia dziesiętne liczby pi , występuje ciąg 0123456789
Okazuje się bowiem, że stosunek sumy dwóch boków podstawy do wysokości piramidy Cheopsa jest właśnie liczbą Pi przybliżoną do czterech miejsc po przecinku. Obwód podstawy piramidy Cheopsa podzielony przez podwójną wysokość daje liczbę Pi = 3,1415. Chociaż sama Piramida Cheopsa stała się obiektem wielu fantastycznych teorii pseudonaukowych, to jednak trzeba jej przyznać, że matematycznie pozostaje prawdziwą zagadką.
Zwolennicy metafizyki, zapewne ucieszą się, że już wśród pierwszych 100 milionów cyfr rozwinięcia liczby Pi znajdą każdą pięciocyfrową liczbę, a z prawdopodobieństwem prawie 2/3 swoją datę urodzenia w formacie DDMMYYYY.
Pierwsze 114 cyfr rozwinięcia dziesiętnego pi daję w sumie liczbę (UWAGA! zakładamy aluminiowe czapeczki) 666, czyli liczby Antychrysta.
A liczba 144 = (6 + 6) x (6 + 6) !!
Na tej stronie można sprawdzić w którym miejscu nieskończonego szeregu pi znajduje się data Twoich urodzin.