Парадокс Паррондо
Можно ли выиграть, играя поочерёдно в две заведомо проигрышные игры?
Оказывается, комбинация проигрышных стратегий может оказаться выигрышной. Это утверждение в теории игр называют парадоксом Паррондо в честь испанского физика, впервые его сформулировавшего.
Более точная с точки зрения математики версия парадокса звучит следующим образом:
В двух играх с зависимыми исходами, в каждой из которых вероятность проигрыша больше вероятности выигрыша, можно построить выигрышную стратегию, манипулируя очерёдностью между ними.
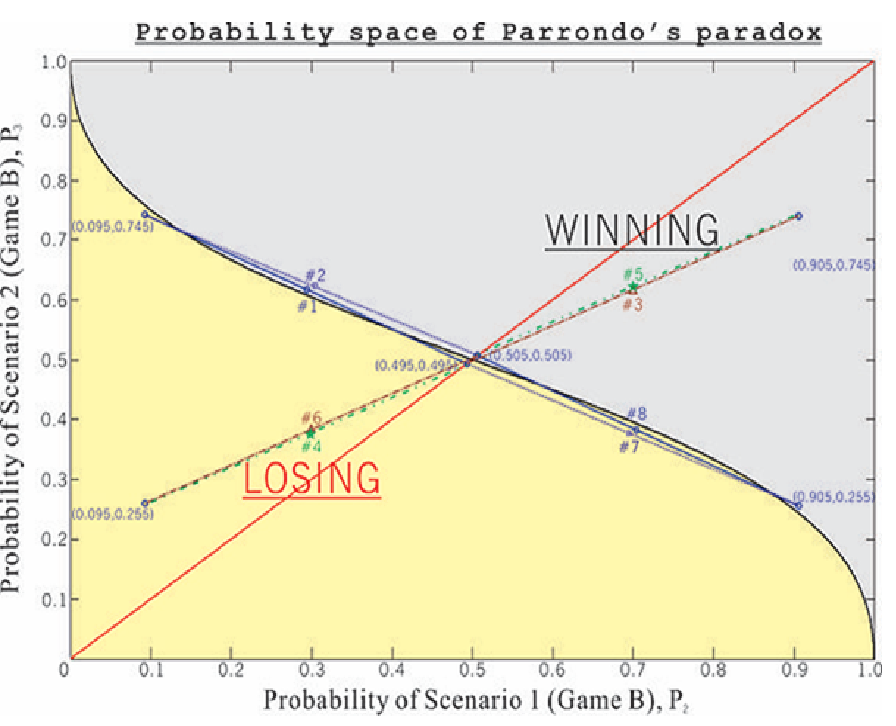
Парадокс заключается в следующем: играя в две специально подобранные игры А и Б, каждая из которых имеет более высокую вероятность проигрыша, чем победы, можно построить выигрышную стратегию, играя в эти игры поочерёдно. То есть, играя в одну игру, в которой на 5 проигрышей выпадает 4 выигрыша, игрок неизбежно проиграет по итогам большого количества розыгрышей. Затем, играя в другую, в которой на 10 проигрышей выпадает 9 выигрышей, игрок также проиграет. Но если чередовать эти игры, например, АББАББ и т.п., то общая вероятность выигрыша может оказаться больше вероятности проигрыша. Условием возникновения парадокса Паррондо является связь между результатами игр А и Б (игры с «капиталом» игрока), либо общий предмет в правилах игры.
После того, как этот парадокс был обнаружен в 1996 г., стали очевидными многие банальные примеры его проявления в жизни.
Например, ситуация с комнатным растением в горшке. Игра А: наливать непрерывно воду в горшок с растением; игра Б: не наливать воду в горшок. С точки зрения сохранения жизни растения обе стратегии проигрышны: растение либо загниёт, либо засохнет. Разумное переключение между играми может сохранить растение живым.
Ситуация с пешеходом, пытающимся добраться на работу вовремя. Игра А: поставить левую ногу на землю; игра Б: поставить правую ногу на землю. Прыгать на одной ноге — проигрышная стратегия, а чередование двух ног может позволить добраться до работы к нужному часу.
Описание нетривиального примера можно найти на сайте «Официальная страница парадокса Паррондо». Игра А состоит в том, что игрок выигрывает $1 (например, в нечестную монетку) с вероятностью
0,5 – ε (ε — положительная достаточно малая величина) и проигрывает $1 с вероятностью 0,5 + ε. Математическое ожидание такой игры составляет $–2ε, т.е. отрицательно.
Игра Б является комбинацией двух игр — Б1 и Б2. Если капитал игрока в начале игры кратен $3, то он играет в Б1, иначе — в Б2.
Игра Б1: игрок выигрывает $1 с вероятностью
0,1 – ε, проигрывает $1 — с вероятностью 0,9 + ε.
Игра Б2: игрок выигрывает $1 с вероятностью
0,75 – ε, проигрывает $1 — с вероятностью 0,25 + ε.
Можно показать, что матожидание игры Б также отрицательно.
Однако, некоторые комбинации игр А и Б обладают положительным ожиданием результата.
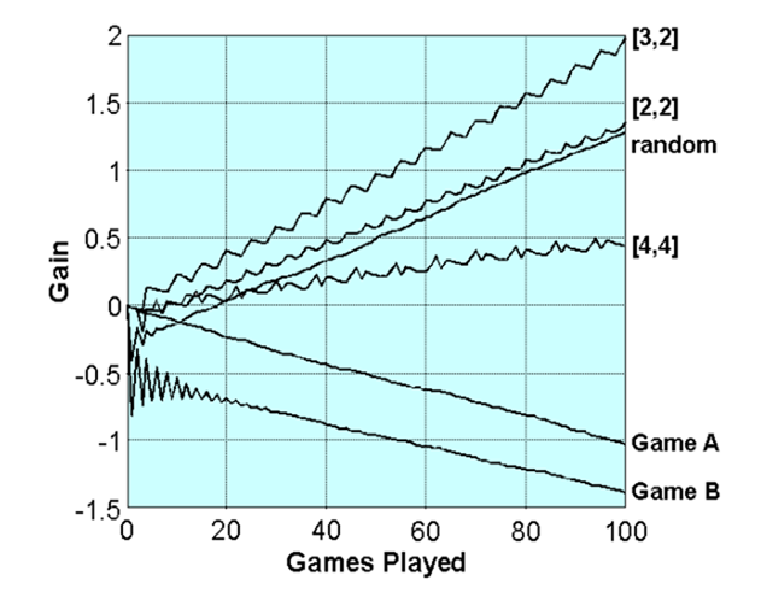
На приведённых графиках показано моделирование игры; [a; b] означает: игра A проводилась a раз, затем игра Б — b раз, а потом всё повторялось; ε = 0,005; при моделировании было проведено более 50 000 запусков игры.
Например, если поочерёдно играть сначала 2 раза в игру А, а потом 2 раза в игру Б, то при ε = 0,005 получается матожидание $0,0148. А если выбор между играми А и Б осуществлять случайным образом, то матожидание составит $0,0147.
Где встречается парадокс Паррондо?
- Финансы. Диверсификация между рискованными активами иногда даёт неожиданную прибыль (но осторожно — это не совет!).
- Биология и экология. Виды могут выживать в изменчивой среде, чередуя стратегии, которые в стабильной среде неэффективны. Некоторые бактерии выживают в токсичной среде, переключаясь между двумя вредными стратегиями метаболизма.
- Социальная политика. Чередование непопулярных реформ может давать позитивный эффект.
Общее свойство игр, в которых возникает парадокс Паррондо, — асимметричное смешивание случайных процессов. В некоторых случаях асимметрия может сделать из хаоса порядок, а из проигрыша — выигрыш. Чередование стратегий приводит к появлению положительной обратной связи: проигрывая в одной игре, вы «переключаетесь» на другую, которая компенсирует потери. Математически это объясняется через марковские цепи и стохастическую стабилизацию: система «застревает» в зонах с положительным матожиданием.
Парадокс Паррондо показывает: мир не всегда линеен. Иногда, чтобы выиграть, нужно научиться правильно проигрывать. Слабости могут стать силой, если их правильно комбинировать. И даже в проигрышных ситуациях есть шанс переломить игру!
Этот парадокс — яркий пример того, как математика разрушает стереотипы. Он учит, что проигрышные стратегии не всегда стоит списывать со счетов — иногда их комбинация становится ключом к успеху. Как говорил Хуан Паррондо: «Не бойтесь плохих игр — бойтесь плохих стратегий».