Парадокс Брейса

Может ли открытие новой дороги в дорожной сети уменьшить её пропускную способность? Или закрытие действующей дороги привести к улучшению трафика?
Контринтуитивные и контрпродуктивные явления подобного типа были описаны немецким математиком Дитрихом Брейсом в 1968 г. Суть их сводится к тому, что добавление дополнительных возможностей к сети (транспортной, компьютерной и т. п.) при самостоятельном и независимом («эгоистическом») распределении нагрузки на её элементы может в некоторых случаях уменьшать эффективность её работы, поскольку равновесие (по Нэшу) такой изменённой сети не обязательно является оптимальным (по Парето).
Рассмотрим пример из Википедии.
Предположим, автомобилисты хотят попасть из пункта Start в пункт End. Имеется два пути — через город A и через город B. Время пути от пункта Start до города A зависит от плотности потока и равно количеству автомобилей (T), делённому на 100. Путь от пункта Start до города B не зависит от количества автомобилей и равен 45 минутам. Аналогично, путь из А в пункт назначения занимает 45 минут, а время в пути от B до пункта назначения равно T/100.
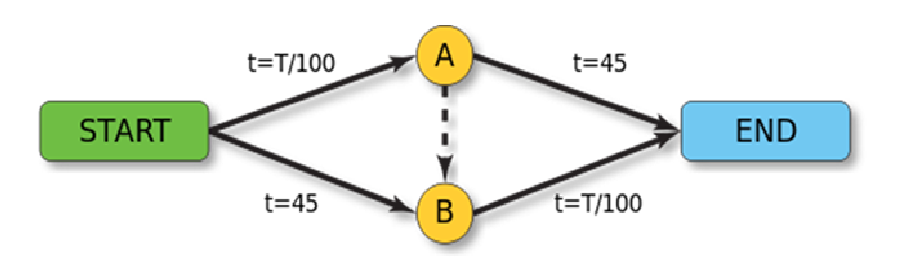
Предположим, что 4000 машин стремятся попасть из точки Start в точку End. Каждая из них выбирает для себя оптимальный маршрут. В силу симметричности ситуации половина машин (2000) выберет путь Start–А–End, а другая половина — путь Start–В–End. Время, затрачиваемое ими на прохождение того и другого пути, равно 65 мин (2000/100 + 45 или 45 + 2000/100).
А теперь представим, что государство решило сократить это время и открыло между точками А и В дополнительную мощную одностороннюю трассу, время прохождения по которой составляет всего 1 мин. Поскольку старые трассы никто не закрывает, то у водителей, теоретически, появляется дополнительный выбор. Но вот парадокс: в этой ситуации все водители выбирают путь Start–А–В–End, поскольку в своей начальной части (Start–А) он составляет всего 40 мин даже в самом худшем варианте (когда все 4000 машин устремляются по нему), тогда как путь Start–В — 45 мин. Дальше выбора опять практически нет, поскольку на путь А–В затрачивается 1 мин, а на путь В–End — опять же в самом худшем варианте — 40 мин. В результате все выбирают путь А–В–End, и общее время прохождения пути Start–А–В–End составляет 81 мин (4000/100 + 1 + 4000/100). То есть общее время прохождения пути между точками А и В увеличивается на 16 мин, хотя, казалось бы, новая трасса была открыта именно для уменьшения этого времени.
Но самое парадоксальное в данной ситуации заключается в том, что сократить это время можно только одним способом — закрыв вновь открытую трассу А–В и вернувшись к старой структуре транспортной сети. К примеру, если разделить машины на два потока и направить половину из них по пути Start–А–В–End, а другую половину — по пути Start–В–End, то ситуация улучшается ненамного, поскольку на прохождение первого затрачивается 65 мин, а на прохождение второго — 81 мин. В среднем получается (65 + 81)/2 = 73 мин. Казалось бы, на первый путь должно затрачиваться всего 41 мин (2000/100 + 1 + 2000/100), а на второй — 65 мин (45 + 2000/100), но здесь не учитывается то, что трасса В–End в этом случае является общей для обоих потоков машин, почему на первый путь и затрачивается 61 мин (2000/100 + 1 + 4000/100), а на второй — 85 мин (45 + 4000/100). То же самое получается, если все машины следуют сначала по трассе Start–А, а в точке А разделяются на два равных потока, один из которых следует по пути А–End, а другой — по пути А–В–End…
Если в сеть из двух дорог добавить третью дорогу, имеющую наименьшую протяженность, происходит нарушение симметрии. Новая третья дорога, будучи самой короткой, кажется с точки зрения водителей самой выгодной и быстрой. И именно этим путём отправляется большее число автомобилей, в результате чего система приобретает новое равновесие. При этом время, которое придётся затратить для достижения финишной прямой, значительно увеличивается. В этом и заключается смысл парадокса Брейса — любой водитель старается думать и действовать оптимальным образом, а увеличение количества дорог приводит к обратному эффекту, чем ожидалось.
Имеется красивая механическая интерпретация парадокса Брейса. На рисунке слева груз подвешен на двух одинаковых пружинках (жёлтого цвета), двух длинных нитях (синих), соединённых ещё короткой (красной) нитью; при этом пружинки соединены последовательно с их общая упругость равна половине упругости каждой отдельной пружины.
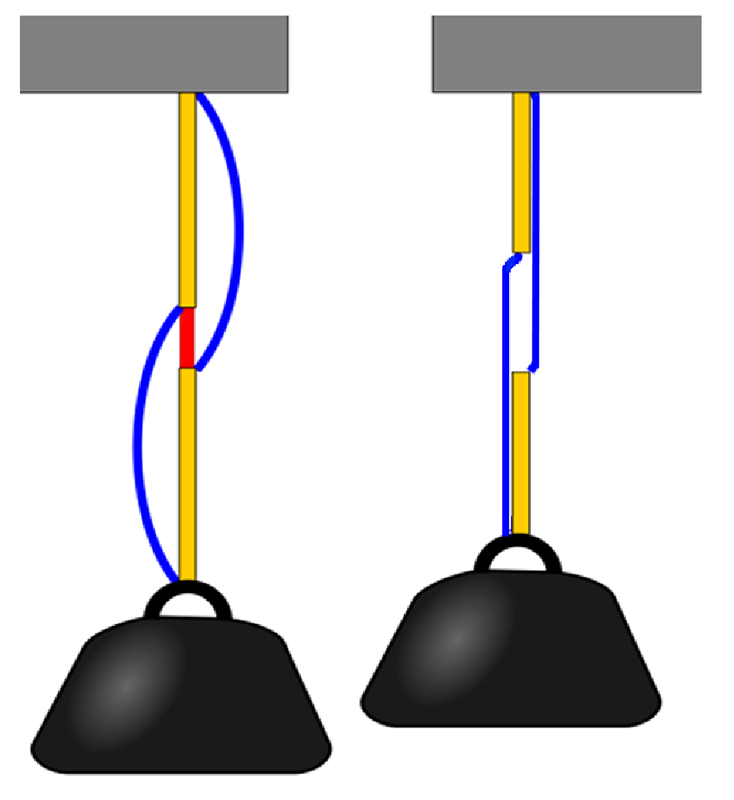
При обрезании красной нити длинные нити натягиваются, а две пружины становятся соединёнными параллельно — коэффициент упругости такой системы в два раза больше, чем у каждой пружины. В результате груз поднимется!
Описано немало примеров из реальной жизни, когда демонтаж некоторых автомагистралей приводил к уменьшению заторов и общему увеличению транспортного потока, и наоборот, строительство новых магистралей или расширение прежних способствовало замедлению трафика.
Например, в 2008 г. автострада в Хьюстоне была расширена до 26 полос, а время в пути увеличилось на 30%.
Физикам удалось зафиксировать парадокс Брейса в полупроводниковой сети — законы транспортировки в этой сети подчиняются законам квантовой механики. Биологи обнаружили действие парадокса Брейса в экологических системах. В частности, если в пищевой цепочке есть вид, обречённый на вымирание, то его удаление может привести к положительному результату, состоящему в предотвращении серии дальнейших вымираний.
И даже в спорте — в его командных видах (баскетболе) — при рассмотрении команды как сети возможностей для забивания мяча в корзину, с разной эффективностью для каждого игрока, звёздный игрок, как оказалось, может снизить общую эффективность команды, подобно тому, как чрезмерно используемый короткий путь увеличивает общее время прохождения через дорожную сеть.
Парадокс Брейса напоминает нам, что даже очевидные вещи бывает полезно подвергать сомнению. И мораль, разумеется, состоит вовсе не в том, что не нужно строить дороги, а в том, что строить их нужно с умом. И нужно уметь договариваться о совместном использовании общих благ — ради получения оптимального для всех результата.