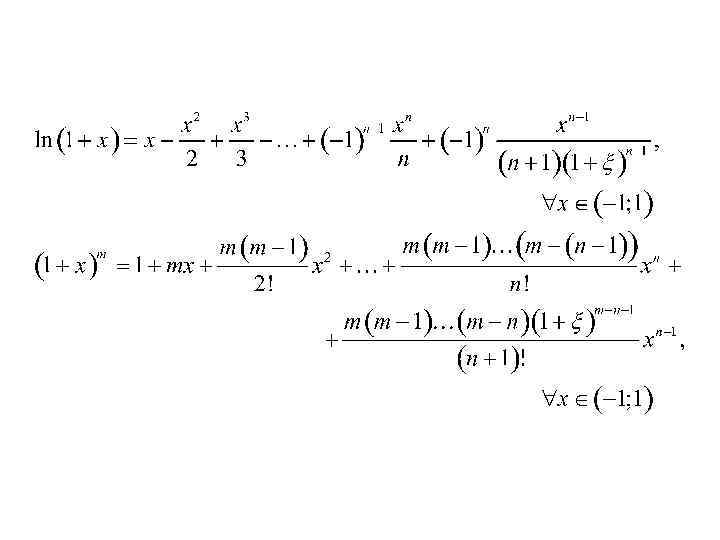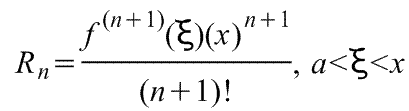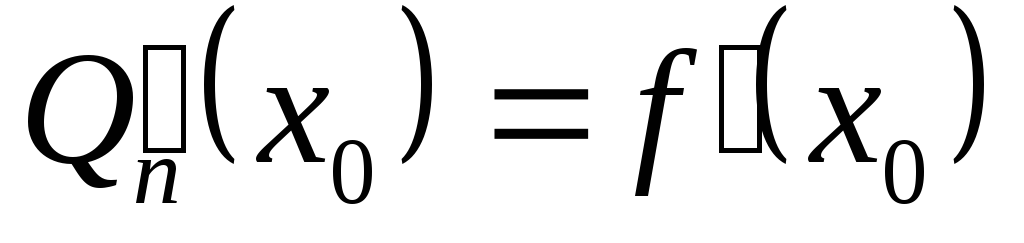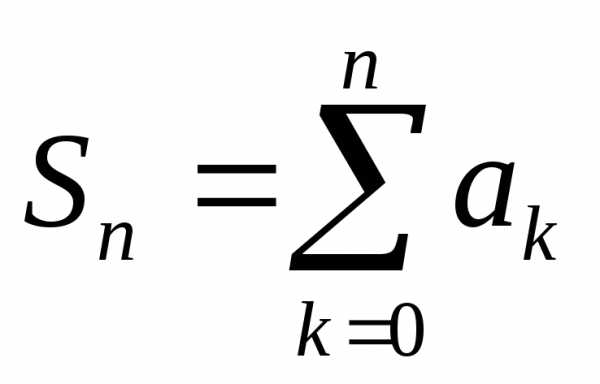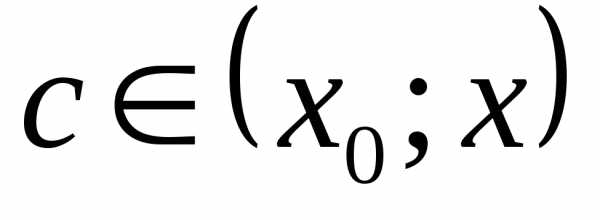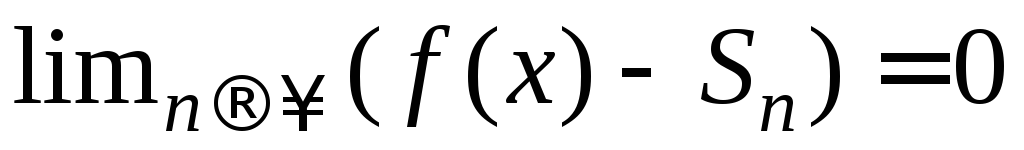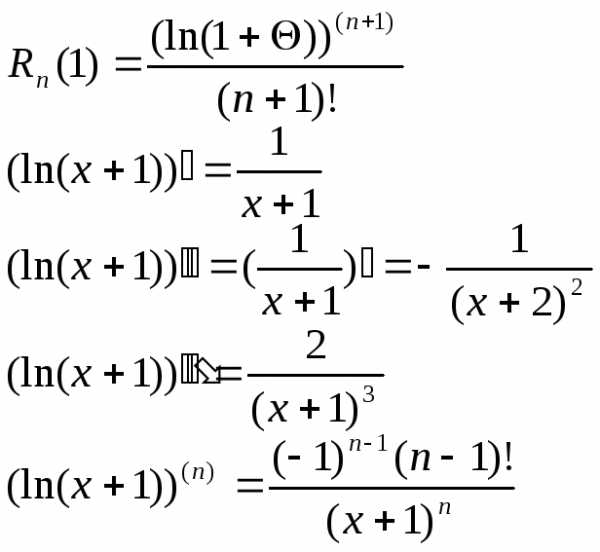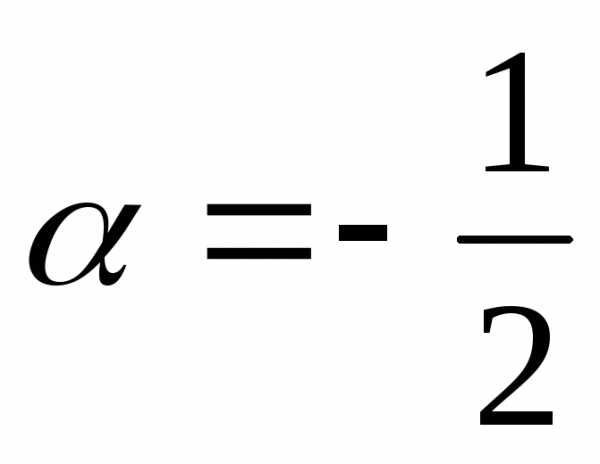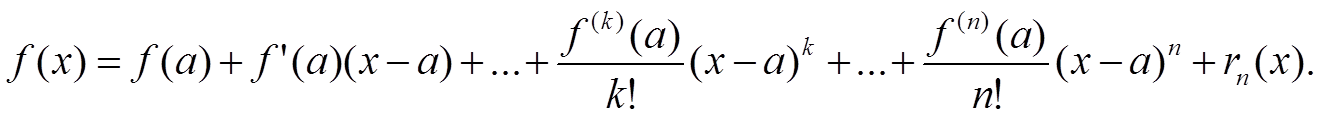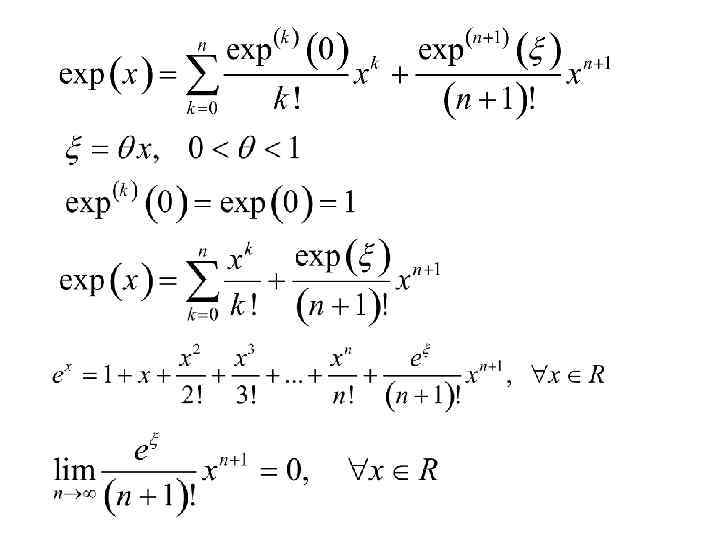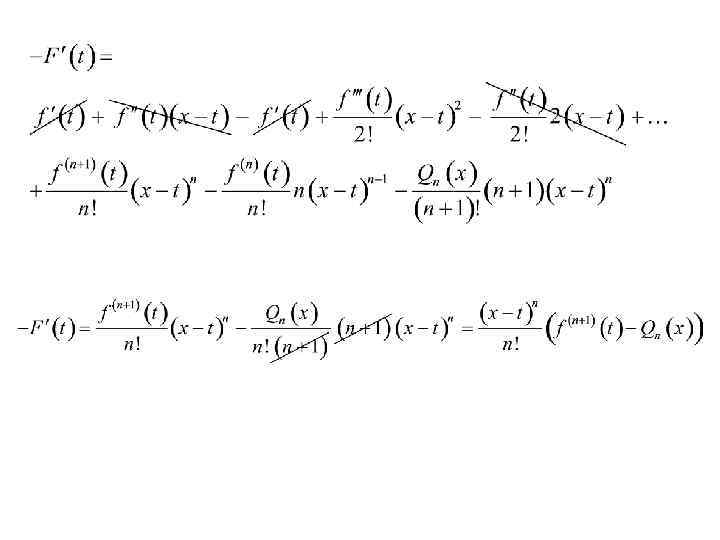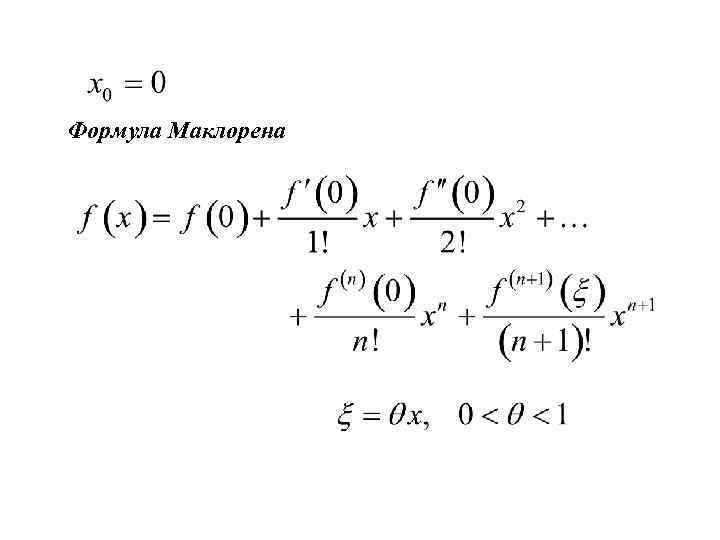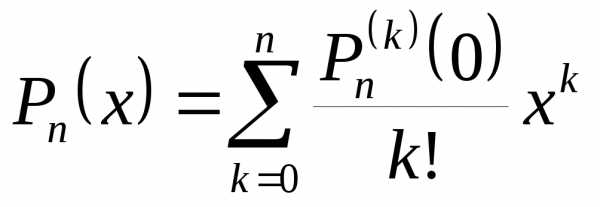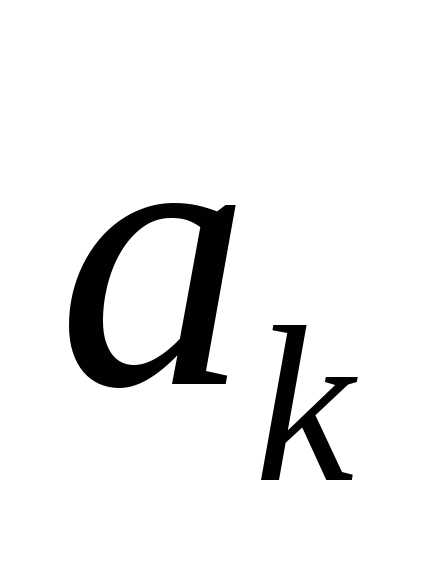Остаточный Член Тейлора

🛑 👉🏻👉🏻👉🏻 ИНФОРМАЦИЯ ДОСТУПНА ЗДЕСЬ ЖМИТЕ 👈🏻👈🏻👈🏻

https://morfey13.wikia.org/ru/wiki/Формула_Тейлора_с...
Остаточный член формулы Тейлора. Пусть . Тогда в некоторой окрестности можно написать равенство. которое называется формулой Тейлора функции в точке , где называется многочленом Тейлора , а - остаточным членом Тейлора …
Формула Тейлора. ( Rn(x) - остаточный член формулы Тейлора). Остаточный член формулы Тейлора. В форме Лагранжа: В форме Коши: В форме Пеано: при. В интегральной форме: Многочлен Тейлора …
www.apmath.spbu.ru/ru/education/final/question03.pdf
Тогда остаточный член r n(x) (см. (4)) для x∈ (x 0 −h,x 0 +h) может быть записан в виде r n(x) = 1 n! Z x x 0 (x−t)nf(n+1)(t)dt. (5) Формула (5) …
Остаточный член в разложении Тейлора. 31.05.2013, 23:50. Последний раз редактировалось h4xx0rus 31.05.2013, 23:50, всего редактировалось 1 раз. "Остаточный член в разложении Тейлора …
https://ru.wikipedia.org/wiki/Ряд_Тейлора
Ориентировочное время чтения: 4 мин
Предположим, что функция имеет все производные до -го порядка включительно в некотором промежутке, содержащем точку . Найдем многочлен степени не выше , значение которого в точке равняется значению функции в этой точке, а значения его производных до -го порядка включительно в точке равняются значениям соответствующих производных от функции в этой точке.

Достаточно …
Предположим, что функция имеет все производные до -го порядка включительно в некотором промежутке, содержащем точку . Найдем многочлен степени не выше , значение которого в точке равняется значению функции в этой точке, а значения его производных до -го порядка включительно в точке равняются значениям соответствующих производных от функции в этой точке.

Достаточно легко доказать, что такой многочлен имеет вид , то есть это -я частичная сумма ряда Тейлора функции . Разница между функцией и многочленом называется остаточным членом и обозначается . Формула называется формулой Тейлора . Остаточный член дифференцируем раз в рассматриваемой окрестности точки . Формула Тейлора используется при доказательстве большого числа теорем в дифференциальном исчислении. Говоря нестрого, формула Тейлора показывает поведение функции в окрестности некоторой точки.

Теорема:

Это формула Тейлора с остаточным членом в общей форме (форма Шлёмильха — Роша).

Различные формы остаточного члена
В форме Лагранжа:

В форме Коши:

В интегральной форме:

Ослабим предположения:
• Пусть функция имеет производную в некоторой окрестности точки и -ю производную в самой точке , тогда:

В асимптотической форме (форме Пеано, локальной форме):
https://portal.tpu.ru/SHARED/k/KONVAL/Sites/Russian_sites/Calc1-ru/6/02.htm
Следовательно, формула Тейлора может использоваться для аппроксимации функций многочленами. При этом остаточный член рассматривается как погрешность …
https://ru.wikipedia.org/wiki/Теорема_Тейлора
Ориентировочное время чтения: 4 мин
Теорема Тейлора для функций от одной вещественной переменной
Формулировка теоремы
Точная формулировка большинства базовых версий теоремы такова.

Теорема Тейлора Пусть k ≥ 1 является целым, и пусть функция f : R → R является k раз дифференцируемой в точке a ∈ R. Тогда существует функция hk : R → R такая, что

Многочлен, возникающий в теореме Тейлора…
Формулировка теоремы
Точная формулировка большинства базовых версий теоремы такова.

Теорема Тейлора Пусть k ≥ 1 является целым, и пусть функция f : R → R является k раз дифференцируемой в точке a ∈ R. Тогда существует функция hk : R → R такая, что

Многочлен, возникающий в теореме Тейлора, является многочленом Тейлора k-го порядка

функции f в точке a.

Теорема Тейлора описывает асимптотическое поведение остаточного члена

который является ошибкой при нахождении приближения функции f с помощью многочленов Тейлора. Используя «O» большое и «o» малое теорему Тейлора можно сформулировать так

Формулы для остатка
Существует несколько точных формул для остаточного члена Rk многочлена Тейлора, наиболее общая из которых следующая.

Остаток в форме среднего значения. Пусть функция f : R → R является k+1 раз дифференцируемой на интервале и непрерывной на отрезке . Тогда Это остаточный член в форме Лагранжа . При тех же условиях Это остаточный член в форме Коши .

Эти уточнения теоремы Тейлора обычно выводятся с помощью формулы конечных приращений.

Можно так же найти и другие выражения для остатка. Например, если G(t) является непрерывной на закрытом интервале и дифференцируемой с нестремящейся к нулю производной на открытом интервале между a и x, то

для некоторого числа ξ между a и x. Эта версия охватывает формы Лагранжа и Коши как частные случаи, и выводится с помощью теоремы Коши о среднем значении (расширенной версии теоремы Лагранжа о среднем значении).

Запись формулы для остатка в интегральной форме является более общей, чем предыдущие формулы, и требует понимания интегральной теории Лебега. Однако она сохраняется также для интеграла Римана при условии, что производная порядка (k+1) от f является непрерывной на закрытом интервале [a,x].

Интегральная форма записи формулы для остатка Пусть f является абсолютно непрерывной на закрытом интервале между a и x. Тогда

Вследствие абсолютной непрерывности f на закрытом интервале между a и x, её производная f существует как L -функция, и это следствие может быть получено с помощью формальных вычислений с использованием теоремы Ньютона — Лейбница и интегрирования по частям.

Оценки остатка
На практике часто бывает полезно численно оценить величину остаточного члена приближения Тейлора.

Будем считать, что f является (k+1)-раз непрерывно дифференцируемой на интервале I, содержащем a. Будем считать, что существуют действительные постоянные числа q и Q такие, что

на всём протяжении I. Тогда остаточный член удовлетворяет неравенству

если x > a, и схожая оценка, если x < a. Это простое следствие из формулы остатка в Лагранжевой форме. В частности, если

на интервале I = (a−r,a+r) с некоторым r>0, то

для всех x∈(a−r,a+r). Второе неравенство называется равномерной оценкой, потому что она сохраняет равномерность для всех x на интервале (a−r,a+r).

Пример
Допустим, мы хотим найти приближение функции f(x) = e на интервале [−1,1] и убедиться, что ошибка не превышает значения 10 . В этом примере считаем, что нам известны следующие свойства экспоненциальной функции:

Из этих свойств следует, что f (x) = e для всех k, и в частности, f (0) = 1. Отсюда следует, что многочлен Тейлора k-го порядка функции f в точке 0 и его остаточного члена в форме Лагранжа даётся формулой

где ξ — это некоторое число между 0 и x. Поскольку e возрастает согласно (*), мы можем использовать e ≤ 1 для x ∈ [−1, 0], чтобы оценить остаток на подынтервале [−1, 0]. Для нахождения верхней границы значения остатка на интервале [0,1], можем использовать свойство e <Балшое Груд Видео
Видео Уроки Королевского Миньета В 3 Дж Бесплатно
Секс Знакомства Семипалатинск
Катя Кабак Обнаженная
Попка Анны Плетневой
Формула Тейлора с остаточным членом в форме …
Формула Тейлора, остаточный член формулы Тейлора ...
3 Формула Тейлора. Различные формы запи- си ос…
Остаточный член в разложении Тейлора : Анализ-I
Ряд Тейлора — Википедия
Формула Тейлора для произвольных дифференцируемых функций
Теорема Тейлора — Википедия
ряд-тейлора / Формула Тейлора. Остаточный член / Математика
Остаточный член в форме Лагранжа
Остаточный член в разложении Тейлора : Анализ-I - Страница 3
Остаточный Член Тейлора