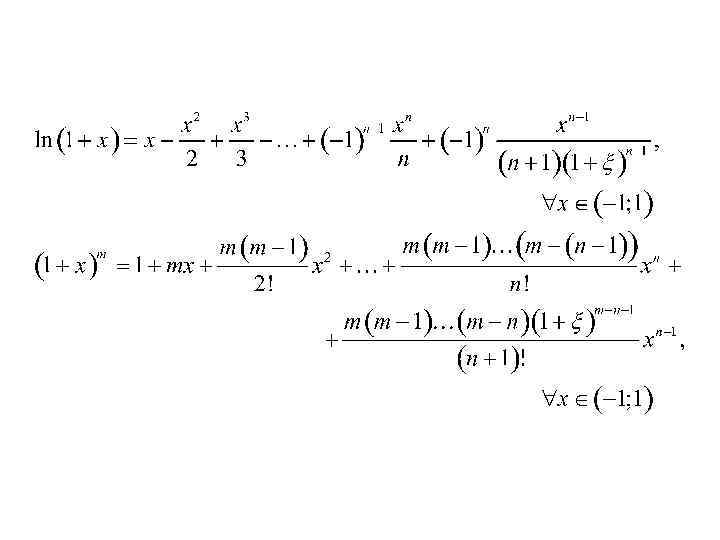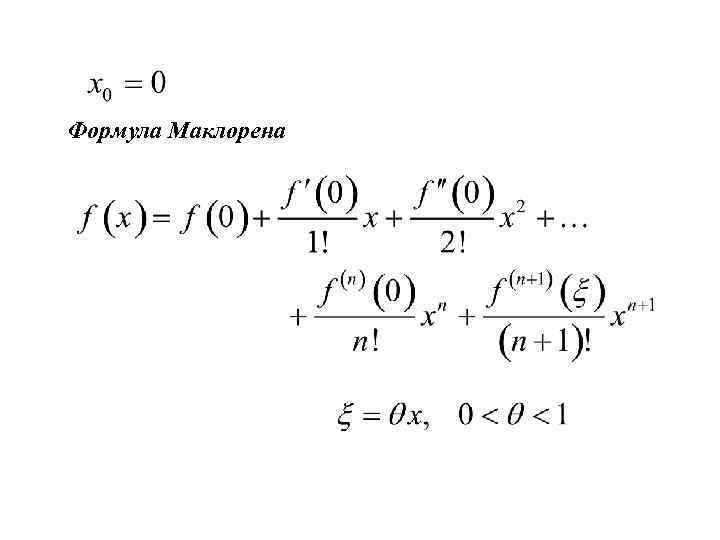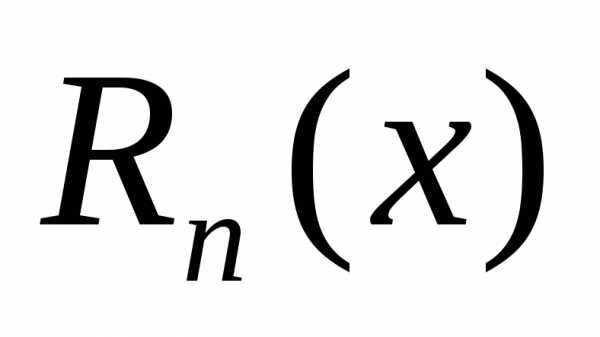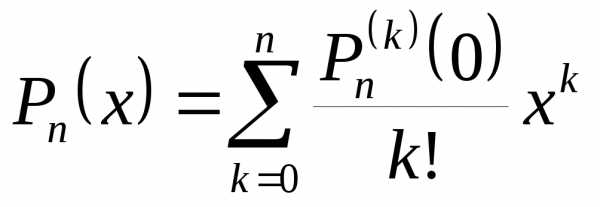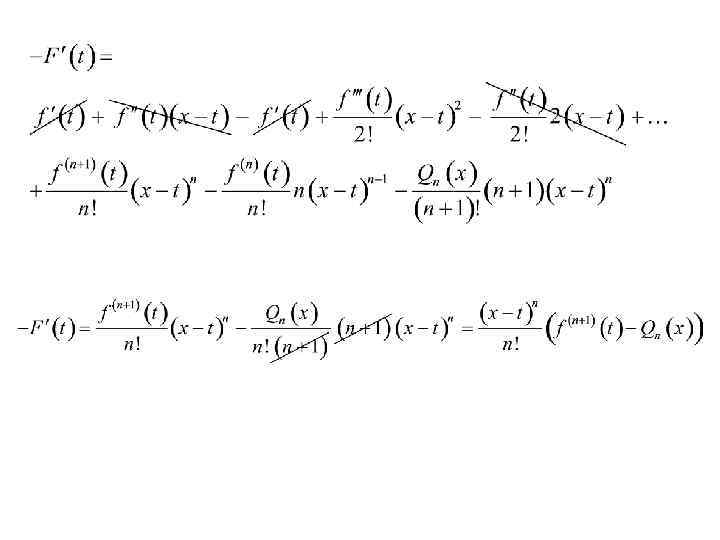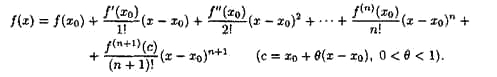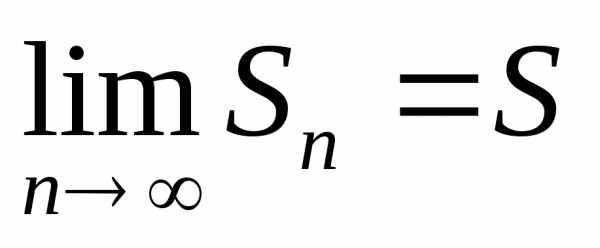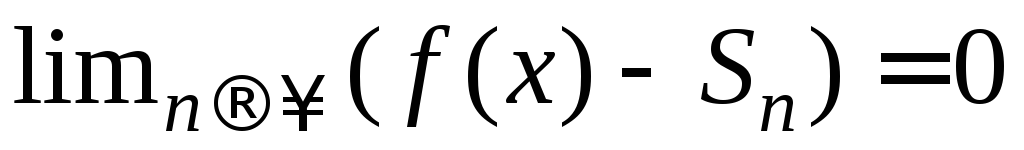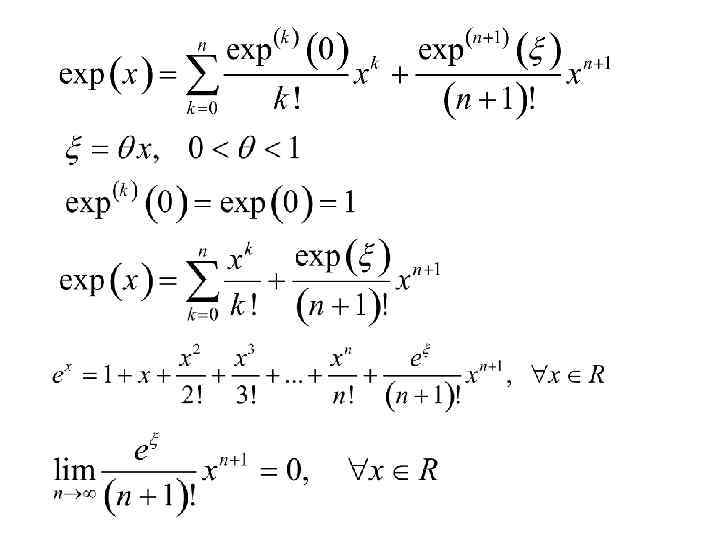Остаточный Член Формулы Тейлора

⚡ 👉🏻👉🏻👉🏻 ИНФОРМАЦИЯ ДОСТУПНА ЗДЕСЬ ЖМИТЕ 👈🏻👈🏻👈🏻

Формула Тейлора с остаточным членом в форме Пеано или Лагранжа.
Править
Пусть . Тогда в некоторой окрестности можно написать равенство
которое называется формулой Тейлора функции в точке , где называется многочленом Тейлора, а - остаточным членом Тейлора (после n-го члена).
то согласно определению сходимости ряда (1) сходится к функции в точке .
Теорема. Формула Тейлора с остаточным членом в форме Лагранжа.
Пусть , непрерывна на отрезке , на интервале . Тогда справедлива формула (1), в которой
Доказательство: будем проводить по индукции, считая . При теорема утверждает, что при некотором
Это утверждение верно, так как оно совпадает с доказанной ранее формулой конечных приращений Лагранжа.
Предположим, что утверждение верно при и установим, что оно верно и при n. Использую теорему Коши о среднем и лемму, имеем (для определенности )
где ,а предпоследнее равенство написано в силу предположения индукции.
О.В Бесов Лекции по математическому анализу.Часть 1. стр.90.
Теорема. Формула Тейлора с остаточным членом в форме Пеано.
Пусть и . Тогда справедлива формула (1), в которой при .
Доказательство: будем проводить по индукции:
При утверждение теоремы верно. В самом деле, в этом случае дифференцируема в точке . Следовательно,
Предположим, что утверждение теоремы верно при и покажем, что это верно и для n.
Использую теорему Лагранжа о конечных приращениях и лемму, имеем (считая для
По предположению индукции при . Следовательно,
О.В Бесов Лекции по математическому анализу.Часть 1. стр.89.
Материалы сообщества доступны в соответствии с условиями лицензии CC-BY-SA, если не указано иное.

Рассмотрим любую функцию , которая имеет непрерывные производные до -го порядка в некоторой окрестности точки . Составим многочлен Тейлора n-й степени по степеням :
совпадает с функцией в точке , но для всех x он не равен . Кроме того,
Здесь – остаточный член формулы Тейлора. Он показывает, какую погрешность мы допускаем при замене на многочлен Тейлора (19.5).
Если функция имеет в окрестности точки непрерывную производную , то для из этой окрестности найдётся точка такая, что
(остаточный член в форме Лагранжа).
Если , то формулу (19.6*) называют формулой Маклорена[2].
Известны и другие формы остаточного члена формулы Тейлора.
Остаточный член в форме Коши: , где .
Поможем написать работу на аналогичную тему
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Формула Тейлора с остаточным членом в смысле Пеано[3]:
Эта формула приспособлена для изучения функции в окрестности точки .

Скачать Порно С Тарай Линн Фокс
1 Ые Съемки В Порно Видео
Порно Рассказы Турок
Бисексуальная Пара Приглашает
Лейла Стар Порно Онлайн
Формула Тейлора, остаточный член формулы Тейлора ...
3 Формула Тейлора. Различные формы запи- си ос…
Формула Тейлора с остаточным членом в форме …
Остаточный член формулы Тейлора
Формула Тейлора для функции
Остаточный член формулы Тейлора — Студопедия
Ряд Тейлора — Википедия
Остаточный член в форме Лагранжа
Остаточный член в разложении Тейлора : Анализ-I
Остаточный Член Формулы Тейлора