О проверке работ ОГЭ

Перейдём к требованиям проверки работ на ОГЭ — они ещё более странные, чем на ЕГЭ.
Например, при решении квадратного неравенства требуется прописывать фразу «неравенство решается графическим методом, с помощью параболы» или «неравенство решается методом интервалов», записывать саму функцию, находить с помощью дискриминанта её нули, указывать направление ветвей параболы. При решении квадратного уравнения ученик не имеет возможности сразу написать корни, найдя их устно — он обязан либо сначала вычислить дискриминант и затем показать, как находятся корни, либо использовать теорему Виета, причём должен написать, что имеется в виду именно обратная теорема. Также ученик не может сразу предъявить форму разложения на множители квадратного трехчлена, даже если она устно видна — он обязан отдельно записать то, как найдены корни. Может быть, при обучении совсем слабых учеников такие требования и можно как-то оправдать. Но точно ли за их невыполнение нужно снимать баллы на экзамене? Справедливости ради отметим, что на ЕГЭ таких диких требований по оформлению при решении квадратных уравнений и неравенств нет.
При введении новой переменной требуется описывать её область значений. Вопрос: зачем? При исследовании уравнений с параметром это требование, конечно, является необходимым. Но при решении обычных уравнений это вопрос чьих-то «хотелок». Вот примеры уравнений, оценённых по этой причине на 0 баллов.

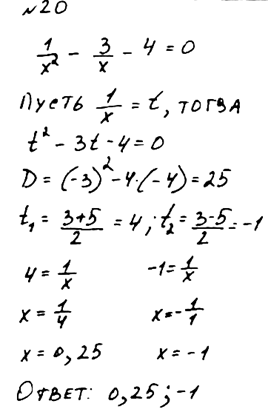
Вот ещё пример решения уравнения, оценённого в 0 баллов.
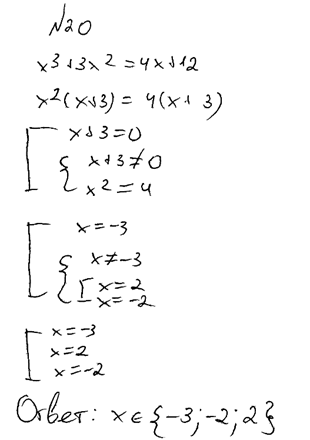
Эксперт конфликтной комиссии сообщил на апелляции, что в приведённом решении «не обоснован переход от кубического уравнения к совокупности уравнений. Слагаемые не перенесены в одну часть, не выполнено разложение на множители, не получено произведение множителей, равное нулю. В совокупности указано ошибочное утверждение x не равен –3, при этом корень x = –3 присутствует в ответе».
Это решение моей ученицы, и мне не стыдно за неё. Но стыдно за этого эксперта и за всю систему проверки.

При решении дробно-рациональных уравнений по текстовым задачам нужно обязательно указывать, при каких значениях переменной оно определено, даже если из смысла задачи и так ясно, что отрицательным или нулевым значение переменной быть не может. Иными словами, пока мы решаем уравнение, мы «забываем задачу» и просто его формально решаем, а потом на другом этапе решения интерпретируем корни уравнения с точки зрения задачи. Аналогично, если ученик решал задачу с помощью системы, то систему нужно решить до конца и получить пару чисел, даже если для ответа на вопрос задачи хватает полученного значения одной переменной. Имеется в виду та же логика: сначала решается система, потом интерпретируется её решение.
Это требование является весьма спорным: имеется немалое количество текстовых задач, в которых невозможно найти все переменные, входящие в уравнение или систему, а только лишь их определённую комбинацию; но именно её-то и спрашивают в задаче. И совершенно непонятно, в чём смысл такого поведения, что на время решения уравнения нужно забывать физический и геометрический смысл входящих в него переменных.
При решении геометрических задач неоправданно жёсткими выглядят требования не просто обязательно ссылаться в каждом, даже самом примитивном утверждении на название теоремы, но и воспроизводить его название, «как в учебнике». Для толкового ребёнка признак «по двум сторонам и углу», очевидно, один, но в такой формулировке он не будет принят, без уточнения, как именно стороны и угол расположены относительно друг друга. При равенстве накрест лежащих углов необходимо обязательно прописывать: 1) название «накрест лежащие», 2) параллельные прямые, 3) секущую. Геометрия, конечно, должна воспитывать ясность мысли, но в том ли состоит эта ясность?
Вот, например, за это решение поставлено 0 баллов за формулировку «по углу и отношению прилежащих сторон» — третий признак подобия положено формулировать «по углу и пропорциональности прилежащих сторон».

В то же время членам предметных комиссий даются рекомендации не придираться к словам «признак» и «свойство», если их формулировки написаны верно, поскольку «дети их часто путают». Вот тут-то как раз можно было бы и «попридираться», поскольку перепутывание этих слов свидетельствует о непонимании самых основ предмета.
За формулировку признака подобия треугольников «по трём углам» эксперты сразу ставят 0 баллов. Такое оценивание на экзамене является чрезмерно строгим, поскольку избыточность формулировки по сути не является математической ошибкой, хотя в процессе обучения и не должна приветствоваться. Примеры избыточных формулировок можно найти и в учебниках. Например, ромб в учебнике определяется как параллелограмм, у которого все стороны равны; прямоугольник — как параллелограмм, у которого все углы прямые.
Очень странная установка состоит в том, что при использовании математического знака подобия между треугольниками необходимо обращать внимание на последовательность букв и снижать балл, если она нарушена, в то время как если два треугольника указываются в свободном тексте, то буквы могут иметь любую последовательность. Сомнительность этого требования заключается в том, что в единственном школьном учебнике геометрии, содержащемся в федеральном перечне, под редакцией Л.С. Атанасяна, соглашение о соответствии вершин в подобных треугольниках не прописано и не используется. Например, рассматривая пропорциональные отрезки в прямоугольном треугольнике АВС с гипотенузой АВ и высотой СD, авторы учебника записывают: ∆ADC ~ ∆CBD.

И это не опечатка в учебнике, выдержавшем более 20 изданий, а вполне сознательная концепция авторов, для которых треугольник, как геометрическая фигура, лишь определённое «множество точек», без какой бы то ни было привязанности к нему его обозначения.
Иной концепции придерживаются авторы других учебников (например, А.В. Погорелов или М.А. Волчкевич), о чём они явно прописывают в своих курсах. Для меня как учителя договор о соответствии вершин при записи подобия треугольников является очень удобным и нужным в процессе обучения школьников. Но названные учебники не входят в федеральный перечень, а соглашение о последовательности букв не является общепризнанным, и, значит, не должно приводить к снижению баллов на экзамене.
Вот ещё одно сомнительное требование от председателя региональной предметной комиссии ГИА-9 по математике Московской области. На вебинаре «Типичные ошибки 9-классников» она обратила внимание на следующее требование. Если ученик пишет фразу «по теореме Пифагора», то необходимо в буквенном виде прописать СУММУ квадратов катетов равных квадрату гипотенузы. Если же при этом будет написан сразу КОРЕНЬ из суммы квадратов (как на слайде), то необходимо снизить оценку на 1 балл.

Самым сложным для учащихся оказывается задание, связанное с построением графиков. И не потому, что это особо трудная тема, а потому, что очень странными являются требования к их экзаменационной проверке. Например, для построения графика линейной функции необходимо задать ровно две точки — не больше и не меньше. Это принято объяснять аксиомой, а наличие третьей точки в таблице интерпретировать, как незнание аксиомы. Хотя непонятно, почему нельзя допустить, что прямая построена не по двум точкам, а на основании геометрического смысла входящих в её уравнение коэффициентов.
Следуя этой логике, можно было бы предположить, что для построения параболы или гиперболы необходимо найти три точки, но это не так! Для параболы эксперты требуют не меньше 5 точек, а для гиперболы — не менее трёх явно найденных точек для каждой ветви. Какое отношение к математике имеет построение графика по точкам вообще не понятно. Гораздо правильнее было бы акцентировать внимание учеников на нахождении координат вершины параболы, асимптот гиперболы, точек пересечении с осями координат. За отсутствие названия функции или названия её графика или неуказание направления ветвей параболы принято сразу ставить 0 баллов.
Примеры подобных оцениваний задач на экзамене есть в копилке у каждого учителя. Проблема в том, что описанные проверки являются не исключением из правила, некоей статистической погрешностью, а самим правилом. Очень странная история состоит в том, что оценивание работ на Едином и Основном государственных экзаменах происходит не в рамках консенсуса научно-педагогического математического сообщества, а по каким-то местечковым понятиям. Очень печально и то, что работы сильных учеников, которые способны сами понять несуразность таких требований и потому находят более адекватные способы оформления решения экзаменационных заданий, не получают должной оценки и во время апелляции.
Бюрократическая система не заинтересована в качественной и прозрачной проверке — проще вех стричь под одну гребёнку. Но в ней заинтересованы наши ученики, учителя, всё общество.
Система не позволяет своим членам воздействовать на неё изнутри: если эксперт проверяет экзаменационные работы не в соответствии с установленными ею правилами, то пути эксперта и системы расходятся. Я для себя решил, что более правильная позиция состоит в том, что с филистерством в образовании лучше бороться, чем становиться его частью.