О формулах и приоритетах
madschumacherСегодня расскажу весьма забавную историю о формулах. В английском языке известна фраза «great minds think alike», что переводится как «великие умы мыслят одинаково». В немецком и русском же фразы отсылают в противоположном направлении: «zwei Dumme, ein Gedanke» (два дурака, одна мысль), или же «у дураков мысли сходятся» не делают чести тем, кто думает одинаково. Но, тем не менее, о таком случае и пойдёт сегодня речь.
Итак, 2015 год, я не так давно поступил в аспирантуру, и с головой окунулся в мир молекулярной динамики (МД). В итоге, к концу года, когда начал считать колебательные спектры, используя МД, обнаружил жуткую вещь: пики всяких валентных C-H, N-H и O-H колебаний, если посчитать траекторию МД с большими шагами, уносит в синюю область (в сторону больших значений частот) по сравнению с гармоническими частотами. Тут явно было что-то не то, поскольку этот синий сдвиг зависел от шага интегрирования. Я много спрашивал про эту хрень у народа на форуме Chemport, но внятного ответа так и не получил (а вместо этого получил много кринжа). В итоге, всё же нашлась статья 2007 года, в которой описывался этот эффект. Всё дело оказалось в ошибке численного интегрирования уравнений движения, и выглядел этот сдвиг вот так:
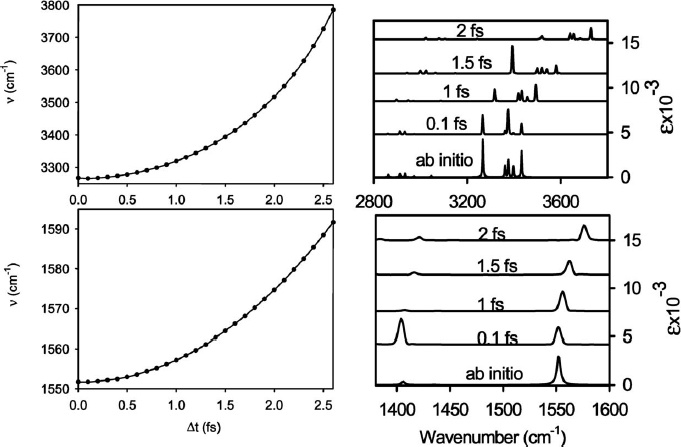
J. Chem. Phys. 127, 084502 (2007) https://doi.org/10.1063/1.2756837
И вроде можно было тему закрывать, но как-то весной 2016-го года (14 марта), балуясь с методом Верле, я нашёл, что можно вывести аналитическое выражение, которое описывает подобный сдвиг. Собственно, вот оно:
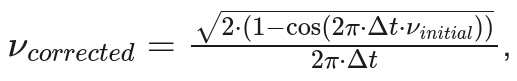
Здесь ν обозначают частоты (начальную и исправленную), а Δt -- шаг интегрирования. Буквально через 5 дней после этого вывода (18 марта), я отослал статью об этом в журнал Journal of Chemical Physics, где она после одного набора комментариев была успешно опубликована 18 апреля 2016 года [J. Chem. Phys. 144, 174108 (2016)]. Несмотря на простоту, формула очень полезная, поскольку позволяет на порядок сократить стоимость МД траектории за счёт выбора гораздо большего шага интегрирования (например, 1 вместо 0.1 фс).
И всё было хорошо, пока я не решил заглянуть как-то раз в статью [J. Chem. Phys. 152, 164105 (2020)], где с удивлением обнаружил эту же самую формулу
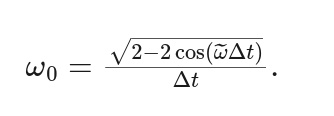
но без ссылки на мою статью. Вместо этого, статья ссылалась на диссертацию Мартина Томаса из университета Бонна. Открыв PDF-ку на сайте этого университета, я сразу же расстроился, поскольку на титульном листе было гордо написано «Октябрь 2015»:

По поиску «arccos», я перешёл в аппендикс сей диссертации, в раздел B4, где увидел вывод очень похожий на мой (только чуть более длинный занудный). В итоге я очень расстроился. Но потом на странице защиты увидел даты самого экзамена:

Диссертация была защищена 12 апреля 2016-го, а опубликована в онлайне вообще 10 июня. Короче, Мартин Томас действительно вывел эту формулу на год, или может даже ещё, раньше, но опубликовал её только в своей диссертации, в то время как другой наглый аспирант опубликовал её в журнале раньше, но почти сразу как её получил.
Мораль сей истории? А не знаю. Но по-моему очень забавная история. Так или иначе, теперь, когда я буду использовать эту формулу, я ещё буду цитировать и соответствующую диссертацию, благо она была опубликована Springer-ом.