Нормальное распределение

Нормальное распределение - это тип непрерывного распределения вероятности случайной величины, которое задаётся так называемой функцией Гаусса.

Попробую объяснить очень упрощённо. У нас есть некий параметр, который распределён нормально, например, рост. Допустим, мы измерили рост вообще всех людей на планете и получили среднее значение (для нашей генеральной совокупности оно будет называться математическое ожидание) и стандартное отклонение. Далее мы можем подставить их в функцию Гаусса и тогда у нас будет уравнение, из которого мы можем посчитать вероятность встретить человека с любым заданным нами ростом. Для людей с ростом ближе к среднему такая вероятность будет больше, а для очень низких или очень высоких людей - меньше.

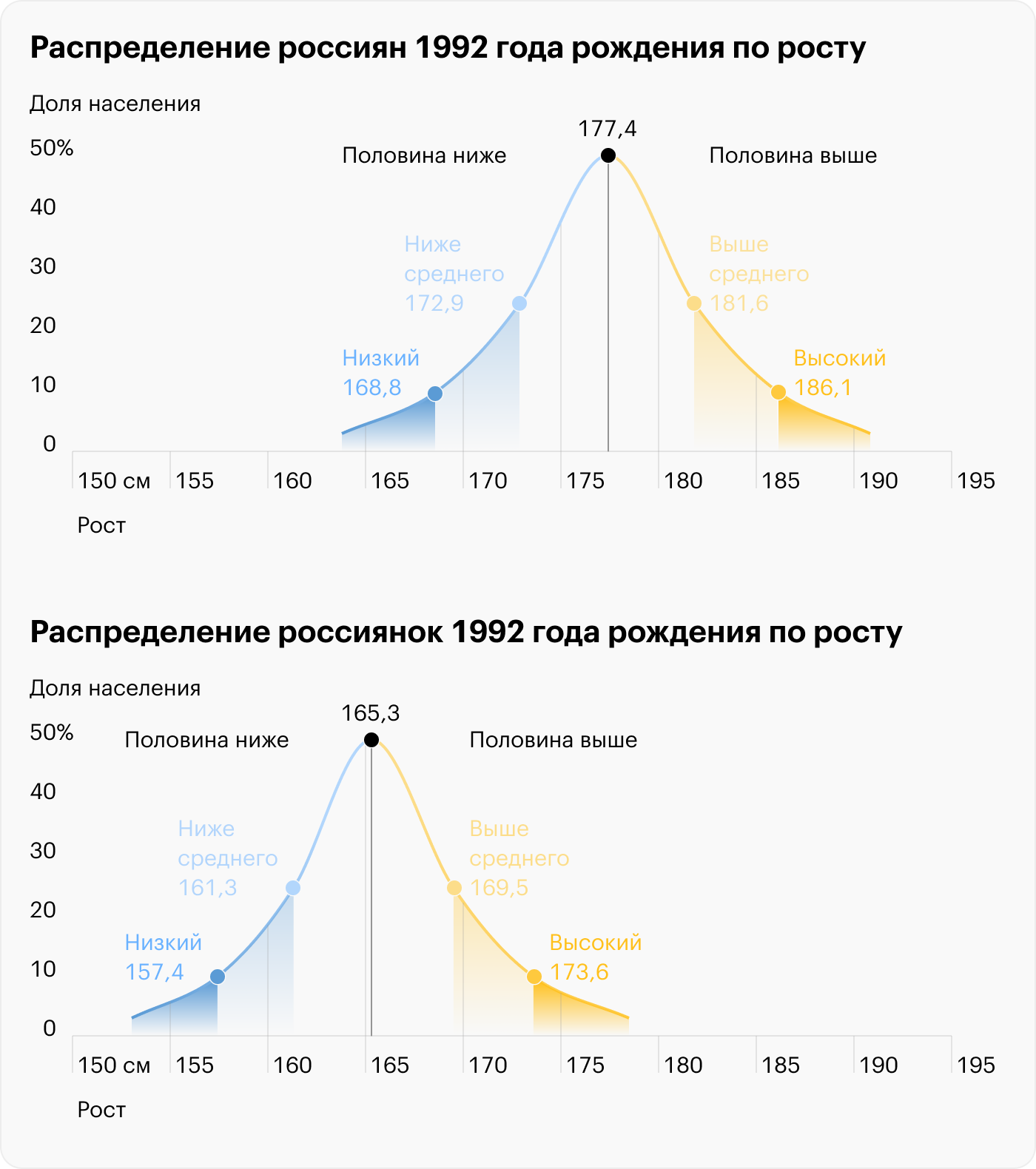
Очень важно, что нормальное распределение может существовать только для непрерывных количественных данных. Дискретные или божеупаси качественные данные такому закону подчиняться не могут. Хотя я регулярно встречаю, как какое-нибудь количество клеток проверяют на нормальность.

Что характерно для нормального распределения:

○ Все меры центральной тенденции (среднее, медиана и мода) совпадают. Что неудивительно, учитывая симметрию распределения.

○ Имеет колоколообразная форму, то есть чем ближе значение к среднему, тем больше вероятность его получить

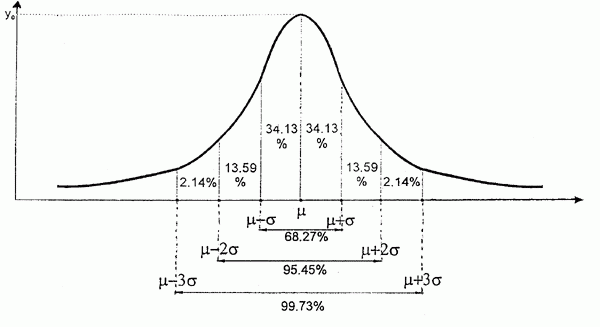
○ Независимо от конкретных значений параметров распределения (математического ожидания и стандартного отклонения) 68,26% данных будет лежать в пределах среднее ± 1 стандартное отклонение; 95,45% в пределах среднее ± 2 стандартных отклонения и 99,73% в пределах среднее ± 3 стандартных отклонения. Это называется правило трёх сигм (в статистике сигма это не одинокий и гордый волк на одинокой дороге, а вполне себе стандартное отклонение).

Правило трёх сигм гласит: вероятность того, что случайная величина отклонится от математического ожидания более чем на 3 стандартных отклонения пренебрежимо мала. И это пожалуй самый грубый способ искать выбросы в выборках: если какое-то значение отклоняется от среднего больше чем на три сигмы - удаляй его. О других способах поиска выбросов я сделаю отдельный пост.

И как же проверить, данные конкретно в твоём эксперименте распределены нормально или нет?

Во-первых, есть графические методы, так сказать "на глазок". Можно построить гистограмму распределения и посмотреть имеет ли она колоколообразную форму. Для гистограммы все значения разбиваются на равные интервалы и считается сколько значений попадает в тот или иной интервал.

Также можно смотреть на график квантиль-квантиль (Q-Q Plot). На этом графике по одной оси отстраиваются квантили теоретического нормального распределения, а по другой оси - квантили твоего распределения. Если точки лежат на одной прямой - всё супер, распределение нормальное, но часто есть отклонения, как правило в районе высоких или низких значений квантили.

Во-вторых, есть статистические тесты. Про то, как работают разные тесты и что такое p-значение я ещё буду писать, а пока перечислю самые основные тесты на проверку нормальности, чтобы если что ты мог найти их в какой-нибудь программе и посчитать уже сейчас. Только помни, что для проверки на нормальность желаемый результат это p>0.05: тогда распределение считается нормальным. Если не понимаешь почему - пока просто поверь, а в будущем я всё расскажу.

○ Критерий Шапиро-Уилка - прекрасно работает на небольших выборках от 3 до 50 значений (хотя как по мне, нормальность на 3 значениях весьма сомнительная штука), для большего количество значений существует модификация - критерий Шапиро-Франчиа

○ Критерий Колмогорова Смирнова - мне кажется наиболее часто встречающийся критерий в русскоязычных статьях, но на самом деле он не является идеальным, поскольку не проверяет соответствие именно нормальному распределению, а вообще любому заданному. Так что лучше использовать критерий Лиллиефорса, который представляет собой критерий Колмогорова-Смирнова заточенный конкретно под нормальность. Но работает он только с большими выборками.

○ Критерий Андерсона-Дарлинга и критерий Крамера-фон Мизеса - более мощные по сравнению с Лиллиефорсом, но так же только для больших выборок.

○ Критерий хи-квадрат Пирсона - не очень хорошо работает, так как очень большая вероятности найти нормальное распределение там, где на самом деле оно не таково. Но зато подойдёт тем, кто очень хочет найти нормальность любой ценой.

Есть ещё куча тестов на нормальность, для искушённых в математике читателей оставлю ссылку, но на мой взгляд Шапиро-Уилка с Андерсоном-Дарлингом для обычной жизни вполне достаточно.

Если твоё распределение оказалось не очень нормальными, то есть два пути: не применять методы анализа, которые используются для нормального распределения, или же преобразовать свои данные в нормальные, воспользовавшись, например, методом Бокса-Кокса. Я с сомнением отношусь к преобразованию экспериментальных данных, но очень часто для big data без него никак, потому что альтернативные методы анализа не то чтобы хорошо разработаны.

В следующих постах расскажу и про другие виды распределения, ведь не единой гауссианой жив учёный.