Нашествие мандаринок или немного о плотной упаковке

Пришла пора, когда прилавки продуктовых отделов ломятся от количества оранжевых цитрусовых, а в больших торговых центрах из них строят целые пирамиды – вот про такие постройки и пойдет сегодня речь.

Зачем нам вообще куда-то упаковывать шары? Ну, кроме того, чтобы красиво выкладывать мандарины на прилавке. На самом деле, эта проблема имеет не только математические, но и вполне «земные» корни, и связана с наукой о кристаллах.

Как понять, что тело является кристаллом, ведь в мире полно «притворщиков» вроде аморфных тел? Один из самых простых способов был открыт в конце XVIII века в результате случайности, когда французский ученый Ренне Гаюи ненароком уронил один из минералов своей коллекции. Присмотревшись к осколкам, он заметил, что отделившиеся кусочки по форме напоминают исходный образец.

Возможно, вы и сами замечали, что крупинки соли порой выглядят как кубики (хотя, надо признать, после обработки они чаще всего круглые). Такая форма является отражением внутренней структуры соли – ее кристаллическая решётка строится из кубических элементов.

Это интересное свойство натолкнуло Гаюи на мысль о том, что все кристаллы состоят из плотно стыкованных элементарных ячеек (невидимых в микроскопы того времени) – форма которых зависит от вещества кристалла. Он отметил, что тогда многообразие твердых тел объясняется не только видом этих маленьких многогранников, но и разными способами их укладки.

Гипотеза Гаюи была верна по отношению к кристаллическим решеткам, но не отвечала на вопрос о том, до какого момента сохраняется эта структура «кирпичиков»: если мы станем делить и делить тело дальше, то обнаружим ли мы, что атомы тоже имеют форму многогранников?

Все в том же XVIII веке англичанин Роберт Гук и голландец Кристиан Гюйгенс обратили внимание, что форма правильных многогранников, присущая кристаллам, может быть построена из сфер. Говоря проще, они считали, что атомы сами по себе все же имеют форму шариков (давайте не будем придираться к таким формулировкам), а угловатая форма тел – лишь следствие их упаковки.

В чем суть: нужно из круглого получить нечто с углами. Начнем мы с двумерного варианта упаковки, где вместо шаров – кружочки. Представьте, что вам выдали монетки одинакового номинала, и одна из них уже лежит на столе.

Вас просят окружить ее со всех сторон другими монетками так, чтобы, во-первых, они симметрично касались центральной, а, во-вторых, чтобы из полученной фигуры можно было бы выложить повторяющийся узор. Собственно, это два основных свойства кристаллических решеток - симметрия и периодичность. Так вот, немного поэкспериментировав, вы скорее всего найдете два основных варианта такой укладки. Первый, где число «контактных» соседей монетки равно четырем. И второй, где семь монеток, одна из которых посередине, а остальные шесть – касаются ее вокруг (рис.1).

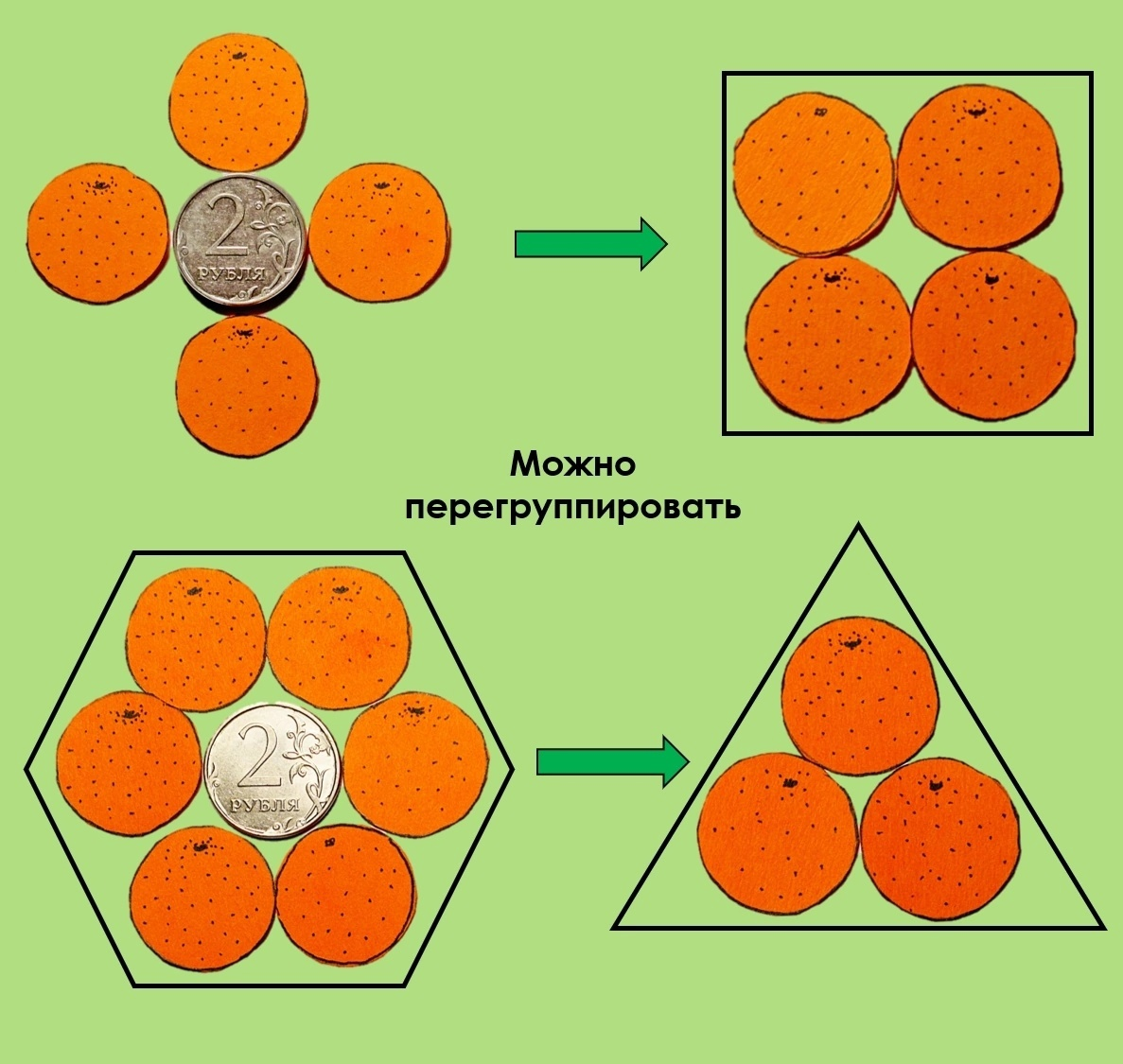
Если обратить внимание на размеры пустот между кружочками в каждом случае, то будет видно, что шестиугольная схема заполняет плоскость эффективнее квадратной, численно это выражается коэффициентом плотности упаковки (рис.2). Так что мне, чтобы вырезать эти плоские мандаринки, сэкономив бумагу, тоже удобно было применить второй вариант (а то бумага нонче дорогая).

Можно заметить, что, если мы продолжим раскладывать узор из полученных элементарных ячеек на плоскости, в больших масштабах мы получим вполне себе красивые прямоугольники, треугольники и так далее. Это как раз то, о чем смог додуматься Гаюи.

Попробуем теперь переместиться в наш трехмерный мандариновый мир и, используя два готовых шаблона, построить что-нибудь объемное. И первый способ, там, где за основу взяты четыре рядом лежащие мандаринки: как нам положить слой сверху? Тривиальный вариант - просто на каждую из четырех пристроить еще по одной, и мы как бы получим фигуру из восьми мандаринок, центры которых формируют куб. Логично, что такой вариант упаковки называется примитивным кубическим, а у каждого цитруса будет по шесть «контактных» соседей (рис. 3).

Однако у такого кубика слишком много воздуха внутри, а наша цель - найти самый плотный вариант для каждой из двумерных схем. Зачем? Как говорится, природа не жалует пустоты: из двух решеток она выберет ту, что наиболее эффективно заполняет пространство. Поэтому несмотря на то, что примитивная кубическая решетка существует (например, таким строением обладают кристаллы пирита) – она не широко распространена, ведь есть более эффективный вариант.

Положим между четырьмя нижними мандаринами один центральный, а сверху снова ряд из четырех. Да, такая конструкция сама по себе держаться не будет, но мы ведь строим лишь одну ячейку нашей решетки – состоящей из огромного количества таких элементов. Так вот, получившийся вариант в виде кубика с одним мандарином в середине называется кубической объемноцентрированной кладкой (ОЦК). Вы можете его представить, как два слоя квадратных ячеек, уложенных в лунки друг друга (рис.3). Такой тип решетки присущ щелочным металлам, например, калию или натрию.

Если с квадратами и кубами разобрались, то поехали дальше к самому главному: плотнейшая упаковка равных сфер. Очевидно, что предыдущие упаковки не являются плотнейшими для трехмерного пространства, если даже в плоском варианте у них не самый высокий коэффициент заполняемости - слишком большие пустоты. Значит, теперь будем отталкиваться от второго варианта с треугольниками и шестиугольниками и попробуем уложить мандарины как можно плотнее.

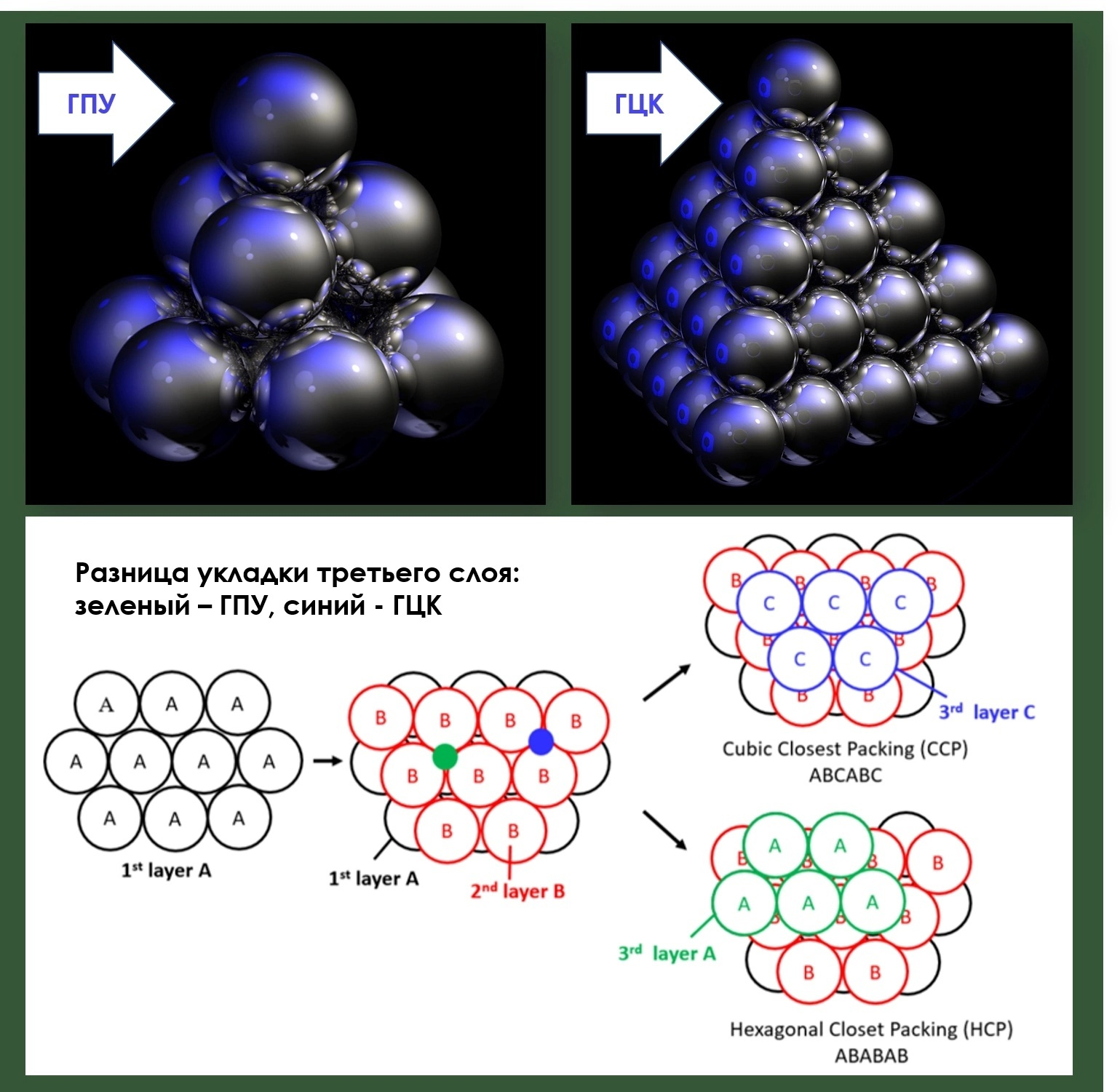
Способ I. Первый слой – шестиугольник из семи мандаринок. Второй слой – три мандаринки в углублениях (рис. 4). Третий такой же как первый – накрывает эту пирамидку сверху. Заметьте, что первый и последний слои идентичны, на изображении видно, что их мандаринки лежат друг напротив друга. Вот такая конструкция, где каждый шарик уложен максимально близко к своим соседям, называется ГЕКСАГОНАЛЬНАЯ ПЛОТНОУПАКОВАННАЯ (ГПУ), собственно, от слова гекса – шесть. ГПУ решеткой обладают титан, бериллий и цинк.

Кажется, что такой вариант единственный, но на самом деле можно уложить мандарины еще одним способом, взяв за основу треугольник.

Способ II. Выстроим пирамидку, где снизу шесть мандаринов, а сверху в ямке лежит еще один. А теперь возьмите вторую точно такую же конструкцию, переверните ее и соедините пирамиды основаниями, соблюдая правила плотной упаковки: каждый шар в углубление между соседними. Конечно, на словах не очень понятно, но я что, зря что ли мандарины тут фотал: на 5й картинке видно, что на этот раз слои сдвинуты друг относительно друга по-другому: они повторяются не через один, а через два ряда. И друг на друга будут смотреть только те угловые мандарины, которые были вершинами изначальных пирамид.

Эта упаковка тоже является плотнейшей, хотя у нее другой порядок повторения слоев, и называется она ГРАНЕЦЕНТРИРОВАННАЯ КУБИЧЕСКАЯ (ГЦК), такой решеткой обладают, например, железо и никель. Что самое удивительное, у обеих конструкций – и у первой, и у второй действительно одинаковая плотность упаковки и количество соседей у каждого шара (12).

Так вот, откуда мы там начинали?.. С кристаллов! Раз уж атомы и молекулы склонны всегда плотненько упаковываться, тогда почему в природе существует целых 14 различных геометрий кристаллических решеток? Ведь судя по всему, даже кубические кладки не самые эффективные, почему же мы не живем в шестиугольном мире? Дело в том, что природа - не математик, и даже мандарины не являются идеальными шарами.

Во-первых, сферы (шары, мандарины), которые мы укладывали вовсе не обязательно имеют одинаковые размеры, а упаковка разновеликих сфер задача уже на порядок сложнее. Во-вторых, если атом можно считать эдаким шариком, то вот с молекулами все интереснее: при соединении одного атома кислорода и двух атомов водорода происходит взаимное проникновение их электронных оболочек. Поэтому молекула воды имеет форму, значительно отличающуюся от шарообразной.

Красивые кристаллические решетки, которые мы рисовали в школе, не совсем точны, ведь их узлы – ядра атомов или центры молекул без учета обычно деформированного электронного облака. Этими причинами и объясняется огромное разнообразие внутреннего строения твердых тел.

Однако, несмотря на то что формально ни Гаюи, ни Гук с Гюйгенсом не были абсолютно верны в своих предположениях, разработанные ими модели оказались очень полезны: подавляющее число металлов (более 75%) имеет один из трех типов решеток – ОЦК, ГЦК или ГПУ (с остальными веществами дела обстоят сложнее).

Сегодня задача о плотной упаковке сфер давно ушла из области физики и кристаллографии: теперь это скорее причудливая забава математиков, рассчитывающих расположение гиперсфер в многомерных пространствах, но все же ее следствия оказались полезны для практики. И пусть природа сложнее и удивительнее упрощенных моделей ученых, важность их открытий нельзя недооценивать.

Надеюсь, теперь вы легко определите тип кладки фруктов на прилавках и будете знать, как рационально разложить снежки для снежной битвы. Плотно пакуйте ваши подарки к Новому году, ешьте мандарины и любите математику :3

P.S. Всех с наступающим!