Método da Bissecção (MATLAB)

(EXERCÍCIO 01) Encontrar a raiz aproximada da equação x^3 - 2*x + 1 = 0, no Intervalo [-2;-1], usando as cinco primeiras iterações. Usar o método da bissecção.

ALGORITMO

function [x] = bisection(f, a, b)

% This function uses the bisection method to find the approximate root of the equation f(x) = 0.

%

% INPUTS:

% f - The function to solve for the root of.

% a - The lower bound of the interval.

% b - The upper bound of the interval.

%

% OUTPUTS:

% x - The approximate root of the equation.

%

% EXAMPLE:

% >> x = bisection(@(x) x^2 - 2*x + 1, 0, 2)

% ans =

% 1.5

% Initialize the counter.

i = 1;

% Initialize the array to store the approximate roots.

x_array = [];

% While the interval is not small enough, iterate.

while (b - a) > 1e-6

% Calculate the midpoint of the interval.

x = (a + b) / 2;

% Add the approximate root to the array.

x_array = [x_array x];

% Display the current iteration.

disp(['The current iteration is:']);

disp(i);

% Check if the function is negative at the midpoint.

if (f(x) < 0)

% If so, update the lower bound of the interval.

a = x;

else

% Otherwise, update the upper bound of the interval.

b = x;

end

% Increment the counter.

i = i + 1;

end

% Return the approximate root.

x = x;

% Display the first five iterations.

disp(['The first five iterations are:']);

disp(x_array(1:5));

end

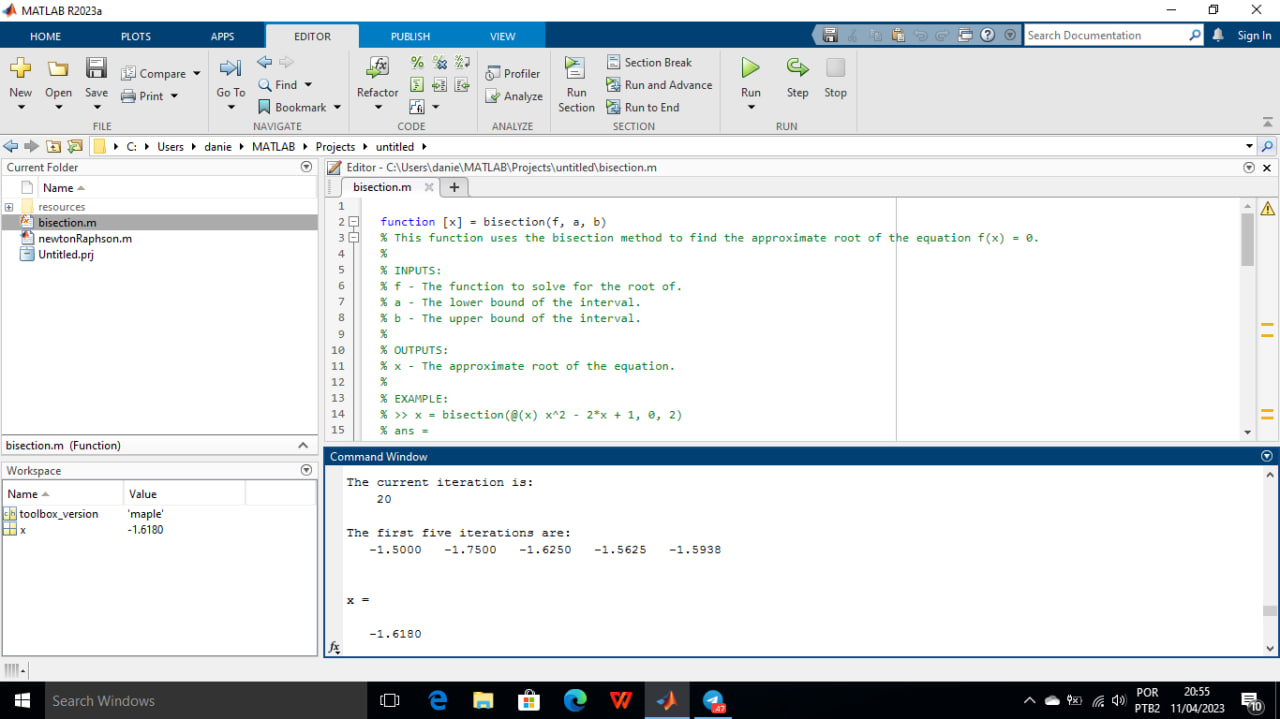
RESPOSTA AO ALGORITMO

Executar usando o comando: x = bisection(@(x) x^3 - 2*x + 1, -2, -1)

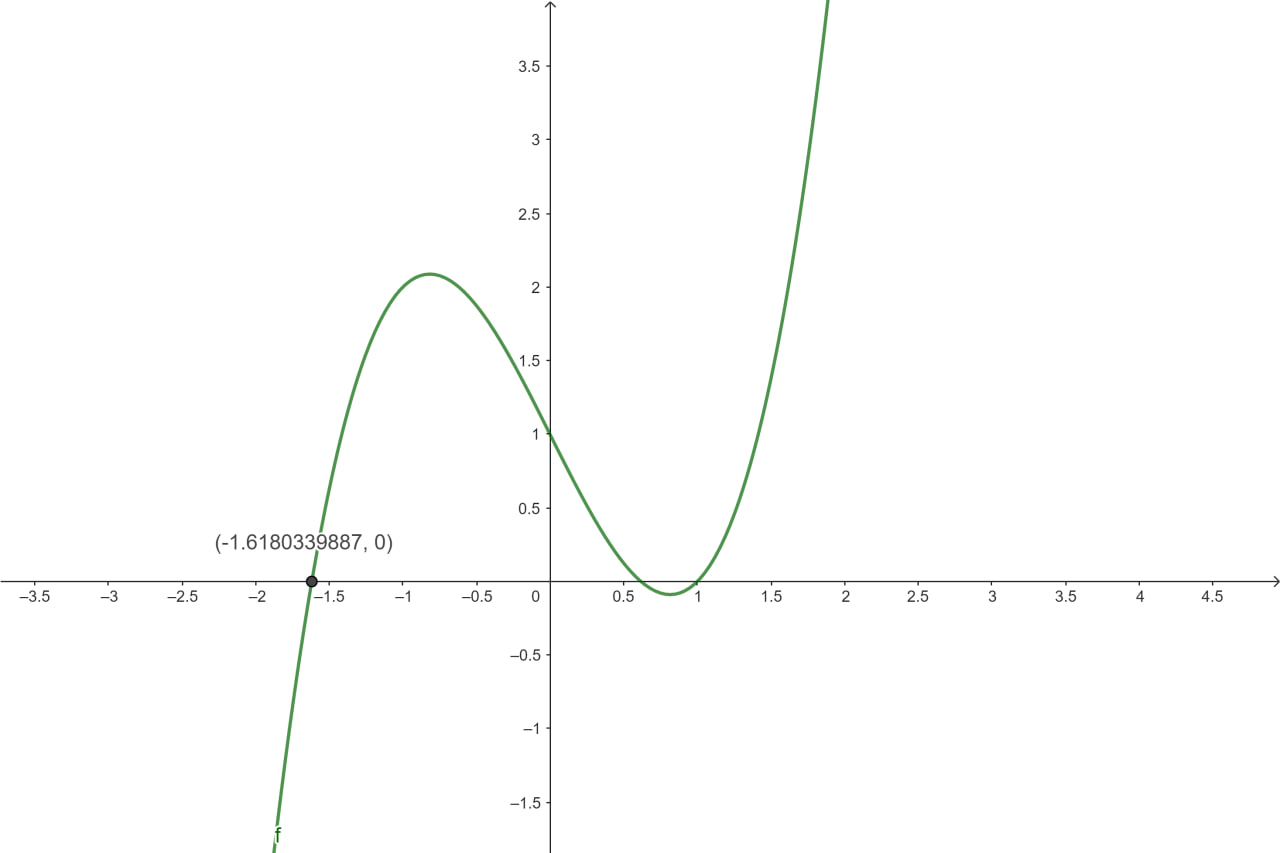
As cinco primeiras iterações são:

  -1.5000  -1.7500  -1.6250  -1.5625  -1.5938

x =  -1.6180

EBOOKS NA AMAZON

Introdução ao Cálculo Numérico em Matlab eBook : Lombaldo, Julio: Amazon.com.br: Livros

Matlab Para Leigos | Amazon.com.br

MATLAB. Curso Completo | Amazon.com.br

Algoritmos E Lógica Da Programação | Amazon.com.br

Amazon.com.br eBooks Kindle: MATLAB: Métodos Numéricos e Gráficos, alves de brito, daniel

Matlab: numerical and graphical methods (English Edition) - eBooks em Inglês na Amazon.com.br