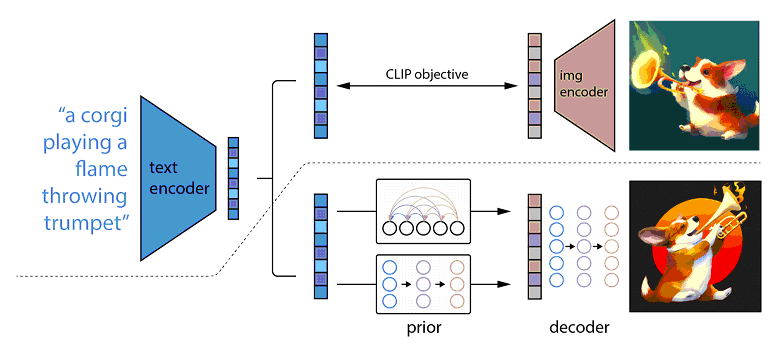
Метод обратной диффузии для генеративных нейросетей

Задача генерации для нейронной сети формулируется следующим образом. Нам нужно генерировать точки многомерного пространства x⁽⁰⁾, статистически распределенные с некоторой плотностью вероятности f(x⁽⁰⁾). Каждая точка x⁽⁰⁾ может быть, например, изображением – тогда координаты многомерного вектора x⁽⁰⁾ отвечают цветам всех пикселей на картинке. Распределение же f(x⁽⁰⁾) показывает, с какой вероятностью всевозможные изображения должны встречаться среди генерируемых. Например, если мы хотим генерировать фотореалистичные изображения велосипедов, то функция f(x⁽⁰⁾) должна принимать высокие значения, лишь когда вектор x⁽⁰⁾ отвечает одному из таких изображений. Для этого компоненты вектора должны удовлетворять множеству сложных условий: цвета пикселей на картинке должны быть демонстрировать как близкие корреляции (например, в некоторых местах давать почти однотонные участки изображения, а в других – наоборот, контрастные переходы), так и дальние корреляции «по смыслу» (например, на изображении велосипеда должно быть ровно два колеса).

В общем, функция f(x⁽⁰⁾) неимоверно сложна и у нас, конечно же, нет для нее готовой формулы. Тем не менее, мы верим, что она существует. Таким образом, задача машинной генерации включает две части:

1) в процессе обучения каким-то образом заставить машину вывести формулу для функции f(x⁽⁰⁾);

2) после этого производить генерацию случайных точек, распределенных с плотностью f(x⁽⁰⁾).

Некоторые программы в явном виде разделяют эти два этапа – например, так делает генератор случайных лиц this-person-does-not-exist.com. В программах же, использующих метод обратной диффузии – таких, как Midjorney, DALL-E и Stable Diffusion, – функция f(x⁽⁰⁾) в явном виде на находится. Она получается лишь в неявном виде, как плотность случайных точек x, осуществляющих определенные блуждания в многомерном пространстве.

Прямая диффузия – такая, как распространение тепла или запахов – может быть смоделирована как блуждание частиц, совершающих на каждом шаге времени случайные шаги. Как правило, такие шаги имеют гауссово распределение N(μ, Σ) со средним значением μ, отвечающим дрейфу, и дисперсией Σ, пропорциональной коэффициенту диффузии. В многомерном пространстве μ становится вектором скорости дрейфа, а Σ – матрицей ковариаций. В простейшем случае равномерной изотропной диффузии μ=0, а Σ пропорциональна единичной матрице. Но, вообще говоря, μ и Σ могут быть функциями координат, и это открывает путь к обратной диффузии.

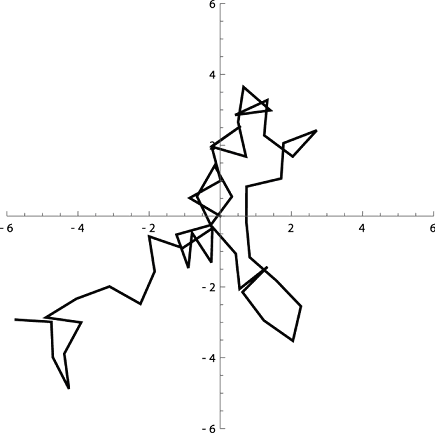
Как было показано Колмогоровым, любому уравнению прямой диффузии, описывающему вероятность того, что частица с координатой x⁽ᵗ⁻¹⁾ в момент времени t–1 окажется в точке x⁽ᵗ⁾ в следующий момент времени t, можно сопоставить сопряженное уравнение, описывающее обратный процесс. Иными словами, существуют два уравнения для прямой и обратной эволюции условной плотности вероятности p(x⁽ᵗ⁾|x⁽ᵗ⁻¹⁾), переходящие друг в друга при обращении времени. Но в уравнении обратной диффузии скорость дрейфа μ и коэффициенты диффузии Σ уже обязательно будут зависеть от координат. А сама форма этой зависимости будет определяться начальной плотностью f(x⁽⁰⁾) облака диффундирующих частиц.

К примеру, если частицы диффундируют во все стороны из начала координат, то скорость дрейфа при обратной диффузии будет направлена обратно, к началу координат. А коэффициент диффузии будет, по мере приближения к началу координат, спадать до нуля, чтобы частицы не убегали от него. Таким образом, процесс обратной диффузии будет заставлять частицы хоть случайно, но статистически целенаправленно двигаться к началу координат, замедляясь и скапливаясь вблизи него.

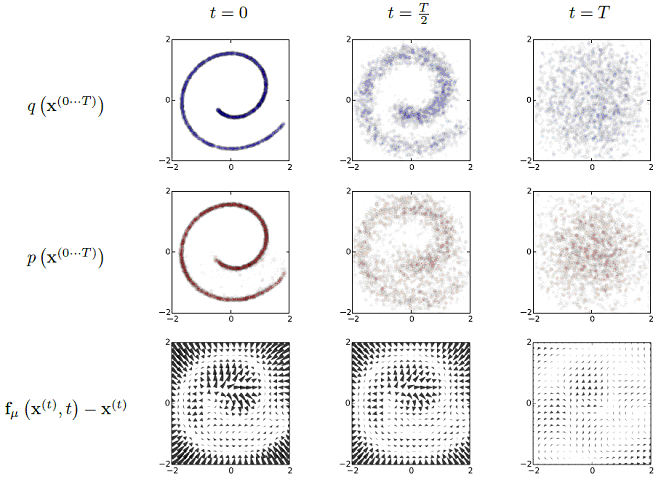
Вот пример для множества частиц на плоскости, которые в начальный момент времени выстроены вдоль спирали. Первая строка диаграмм показывает прямую диффузию, приводящую к изотропному расплыванию облака частиц. Вторая строка показывает обратную диффузию, только смотреть на диаграммы нужно справа налево, потому что время здесь идет в обратном направлении. Это не просто повторение картинок с прямой диффузией, а самостоятельно смоделированный процесс обратных блужданий. Третья строка показывает векторное поле скорости дрейфа при обратной диффузии: видно, как стрелки постепенно направляют частицы к точкам спирали.

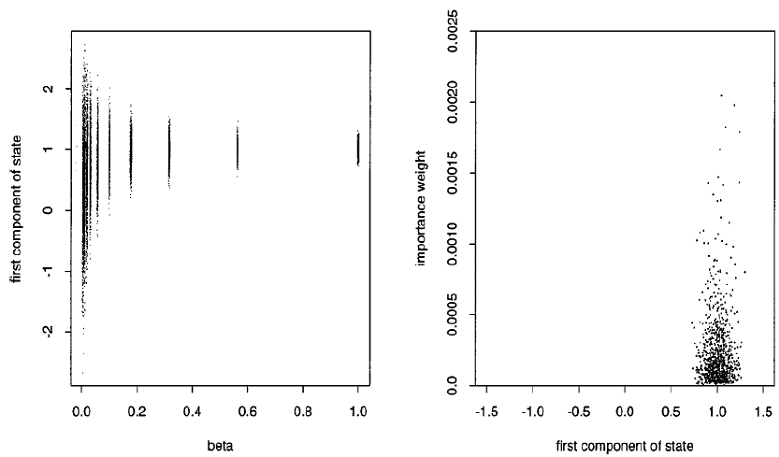
Кстати говоря, обратная диффузия имеет параллели с так называемой отжигаемой выборкой по значимости (annealed importance sampling) – методом Монте-Карло, при котором нам нужно выбрасывать точки с плотностью, задаваемой распределением Гиббса ~exp(–H(x)/T). В отличие от обычного алгоритма Метрополиса, выбрасывающего каждую точку x⁽ᵗ⁾ на основе предыдущей x⁽ᵗ⁻¹⁾, в этом методе генерация каждой точки начинается «с нуля»: сначала мы считаем, что система имеет очень высокую температуру, а потом, параллельно моделированию случайных шагов, постепенно снижаем температуру до текущей T (как при симулированном отжиге). Иными словами, метод отжигаемой выборки по значимости дает нам способ постепенного превращения, при помощи случайных блужданий, облака точек с исходной плотностью распределения (высокотемпературной) в облако точек с целевой плотностью (распределение Гиббса при температуре T). На рисунке показан пример того, как широкое облако постепенно превращается в более узкое. В принципе, ту же задачу решает и метод обратной диффузии.

Метод генерации изображений при помощи обратной диффузии устроен следующим образом. Каждое изображение отвечает многомерному вектору x, то есть некой частице, находящейся где-то в пространстве цветов всех пикселей. Мы берем случайную точку x⁽ᵀ⁾, которую можно считать результатом прямой диффузии – координатой частицы в конечный момент времени t=T. А для обратной диффузии это, наоборот, начальное условие, приводящее, после последовательности блужданий, к искомой точке x⁽⁰⁾. Если мы будем брать множество различных точек x⁽ᵀ⁾, то, повторяя каждый раз процесс обратной диффузии, мы получим множество точек x⁽⁰⁾, распределенных с плотностью f(x⁽⁰⁾), описывающей статистику реалистичных изображений.

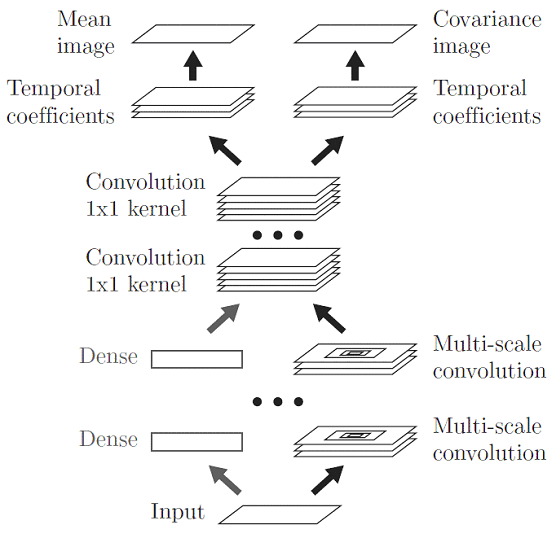
Самый главный вопрос – где для обратной диффузии взять скорости дрейфа μ и матрицы ковариаций Σ, зависящие от многомерных координат. Эти функции генерируются нейронной сетью, потому что нейросети как раз хорошо подходят для универсальной аппроксимации многомерных функций. Нейронную сеть можно обучать, подгоняя веса ее межнейронных связей таким образом, чтобы процесс обратной диффузии вел нас в верном направлении.

Обучение, как обычно, проводится минимизацией некоторой функции ошибок, которую можно найти, если у нас имеется достаточно большая и репрезентативная библиотека изображений нужного нам типа – то есть векторов x⁽⁰⁾, встречающихся с плотностью вероятности, близкой к целевой плотности f(x⁽⁰⁾). Вот пример изображений, генерируемых обратной диффузией после обучения нейросети на библиотеки изображений рукописных цифр MNIST. Как видно, они (в большинстве) достаточно реалистичны и при этом не совпадают с библиотечными, то есть каждое изображение уникально.

Вот еще пример: слева показаны несколько изображений из библиотеки маленьких картинок CIFAR-10, а справа – результаты генерации методом обратной диффузии. Видно, что, хотя сгенерированные картинки зачастую бессмысленны, статистически – в плане того, как цвета пикселей соотносятся между собой на малых и на больших расстояниях – они похожи на реальные.

Наконец, еще один момент, важный для практической генерации изображений – это необходимость направлять процесс обратной диффузии. Если мы хотим получить картину типа «кот верхом на динозавре скачет по поверхности Луны», нам нужно сгенерировать не просто случайное реалистичное изображение, а изображение, находящееся в определенной области многомерного пространства. То есть, обратную диффузию нужно как-то подтолкнуть в нужном нам направлении.

Самый простой пример, приведенный в статье, следующий: допустим, что мы хотим дорисовать (inpaint) отсутствующую часть изображения при помощи метода обратной диффузии. Если у нас имеется уже обученная программа, умеющая генерировать, при помощи случайных блужданий, реалистичное, но случайное изображение x⁽⁰⁾ по начальной точке x⁽ᵀ⁾(это может быть картинка с белым шумом), то нужно сделать следующее. Мы ограничиваем процесс диффузии той областью пространства векторов x, для которых часть цветов пикселей должна совпадать с цветами пикселей имеющейся части изображения, которое нужно дорисовать. Иными словами, мы ограничиваем обратную диффузию определенной гиперплоскостью в многомерном пространстве.

Вот пример, где используется модель, уже обученная на библиотеке фотографий древесной коры. Первая картинка показывает исходное изображение древесной коры, а на второй центральный квадрат заменен случайным шумом – мы его хотим восстановить при помощи программы. Второе изображение берется в качестве начальной точки x⁽ᵀ⁾обратной диффузии. При этом диффузия может идти лишь только в том подпространстве векторов (или подмножестве изображений), у которых цвета всех нетронутых пикселей, окружающих зашумленный квадрат, зафиксированы. Результат обратной диффузии показан на третьей картинке: центральная часть изображения, которой мы разрешили блуждать, дошла до реалистичного состояния. Видно, что она не только плавно стыкуется с окружающей корой, но и правильно воспроизводит как мелкую, так и крупномасштабную геометрическую структуру трещин.

Это простой пример направленной обратной диффузии, а в современных генеративных моделях все уже гораздо сложнее. Для того, чтобы создавать изображения по словесному описанию, используется отдельная нейросеть, работающая с этим описанием и затем выводящая набор параметров, направляющих диффузию в нужную сторону. Как именно это происходит – отдельная большая тема. Кроме того, к изображению могут применяться дополнительные фильтры и прочие улучшители, доводящие его до полной реалистичности, а к словесным описаниям могут применяться и цензурные фильтры.