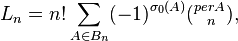Latin Square

⚡ 👉🏻👉🏻👉🏻 INFORMATION AVAILABLE CLICK HERE 👈🏻👈🏻👈🏻

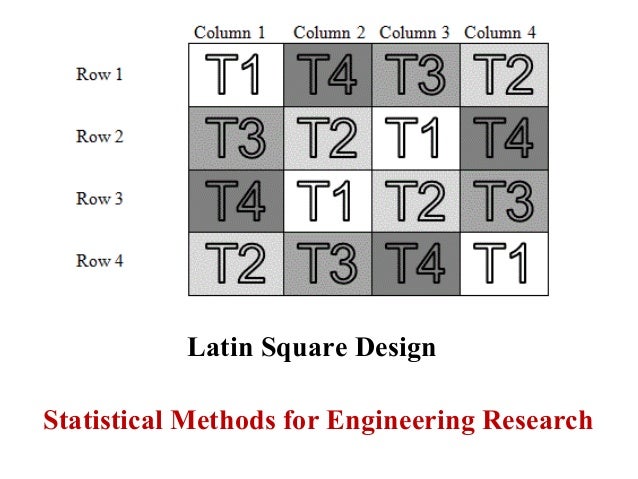
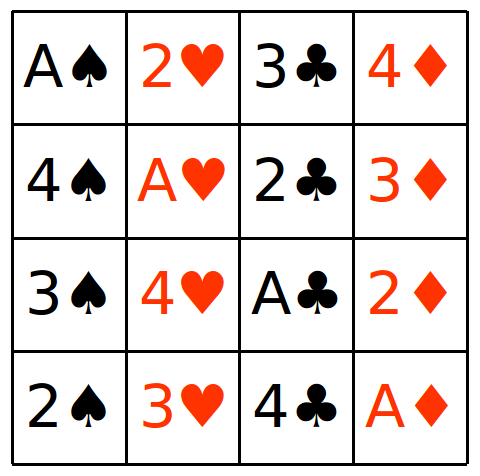
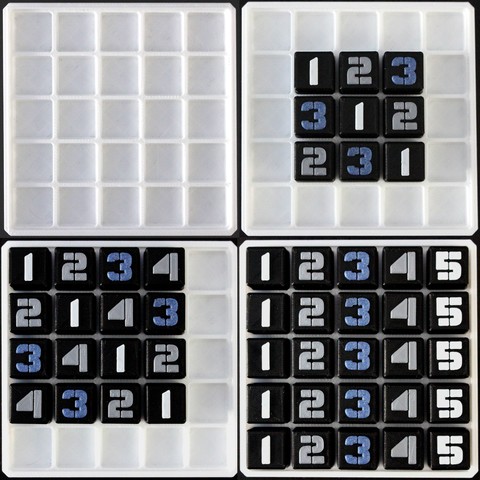
In combinatorics and in experimental design, a Latin square is an n × n array filled with n different symbols, each occurring exactly once in each row and exactly once in each column. An example of a 3×3 Latin square is
The name "Latin square" was inspired by mathematical papers by Leonhard Euler (1707–1783), who used Latin characters as symbols,[1] but any set of symbols can be used: in the above example, the alphabetic sequence A, B, C can be replaced by the integer sequence 1, 2, 3. Euler began the general theory of Latin squares.
The Korean mathematician Choi Seok-jeong was the first to publish an example of Latin squares of order nine, in order to construct a magic square in 1700, predating Leonhard Euler by 67 years.[2]
A Latin square is said to be reduced (also, normalized or in standard form) if both its first row and its first column are in their natural order.[3] For example, the Latin square above is not reduced because its first column is A, C, B rather than A, B, C.
Any Latin square can be reduced by permuting (that is, reordering) the rows and columns. Here switching the above matrix's second and third rows yields the following square:
This Latin square is reduced; both its first row and its first column are alphabetically ordered A, B, C.
If each entry of an n × n Latin square is written as a triple (r,c,s), where r is the row, c is the column, and s is the symbol, we obtain a set of n2 triples called the orthogonal array representation of the square. For example, the orthogonal array representation of the Latin square
where for example the triple (2, 3, 1) means that in row 2 and column 3 there is the symbol 1. Orthogonal arrays are usually written in array form where the triples are the rows, such as:
The definition of a Latin square can be written in terms of orthogonal arrays:
This means that the n2 ordered pairs (r, c) are all the pairs (i, j) with 1 ≤ i, j ≤ n, once each. The same is true of the ordered pairs (r, s) and the ordered pairs (c, s).
The orthogonal array representation shows that rows, columns and symbols play rather similar roles, as will be made clear below.
Many operations on a Latin square produce another Latin square (for example, turning it upside down).
If we permute the rows, permute the columns, and permute the names of the symbols of a Latin square, we obtain a new Latin square said to be isotopic to the first. Isotopism is an equivalence relation, so the set of all Latin squares is divided into subsets, called isotopy classes, such that two squares in the same class are isotopic and two squares in different classes are not isotopic.
Another type of operation is easiest to explain using the orthogonal array representation of the Latin square. If we systematically and consistently reorder the three items in each triple (that is, permute the three columns in the array form), another orthogonal array (and, thus, another Latin square) is obtained. For example, we can replace each triple (r,c,s) by (c,r,s) which corresponds to transposing the square (reflecting about its main diagonal), or we could replace each triple (r,c,s) by (c,s,r), which is a more complicated operation. Altogether there are 6 possibilities including "do nothing", giving us 6 Latin squares called the conjugates (also parastrophes) of the original square.[4]
Finally, we can combine these two equivalence operations: two Latin squares are said to be paratopic, also main class isotopic, if one of them is isotopic to a conjugate of the other. This is again an equivalence relation, with the equivalence classes called main classes, species, or paratopy classes.[4] Each main class contains up to six isotopy classes.
There is no known easily computable formula for the number Ln of n × n Latin squares with symbols 1,2,...,n. The most accurate upper and lower bounds known for large n are far apart. One classic result[5] is that
A simple and explicit formula for the number of Latin squares was published in 1992, but it is still not easily computable due to the exponential increase in the number of terms. This formula for the number Ln of n × n Latin squares is
where Bn is the set of all n × n {0, 1} matrices, σ0(A) is the number of zero entries in matrix A, and per(A) is the permanent of matrix A.[6]
The table below contains all known exact values. It can be seen that the numbers grow exceedingly quickly. For each n, the number of Latin squares altogether (sequence A002860 in the OEIS) is n! (n-1)! times the number of reduced Latin squares (sequence A000315 in the OEIS).
5,524,751,496,156,892,842,531,225,600
9,982,437,658,213,039,871,725,064,756,920,320,000
5,363,937,773,277,371,298,119,673,540,771,840
776,966,836,171,770,144,107,444,346,734,230,682,311,065,600,000
For each n, each isotopy class (sequence A040082 in the OEIS) contains up to (n!)3 Latin squares (the exact number varies), while each main class (sequence A003090 in the OEIS) contains either 1, 2, 3 or 6 isotopy classes.
The number of structurally distinct Latin squares (i.e. the squares cannot be made identical by means of rotation, reflexion, and/or permutation of the symbols) for n = 1 up to 7 is 1, 1, 1, 12, 192, 145164, 1524901344 respectively (sequence A264603 in the OEIS) .
We give one example of a Latin square from each main class up to order five.
They present, respectively, the multiplication tables of the following groups:
A transversal in a Latin square is a choice of n cells, where each row contains one cell, each column contains one cell, and there is one cell containing each symbol.
One can consider a Latin square as a complete bipartite graph in which the rows are vertices of one part, the columns are vertices of the other part, each cell is an edge (between its row and its column), and the symbols are colors. The rules of the Latin squares imply that this is a proper edge coloring. With this definition, a Latin transversal is a matching in which each edge has a different color; such a matching is called a rainbow matching.
Therefore, many results on Latin squares/rectangles are contained in papers with the term "rainbow matching" in their title, and vice versa.[7]
Some Latin squares have no transversal. For example, when n is even, an n-by-n Latin square in which the value of cell i,j is (i+j) mod n has no transversal. Here are two examples:
In 1967, H. J. Ryser conjectured that, when n is odd, every n-by-n Latin square has a transversal.[8]
In 1975, S. K. Stein and Brualdi conjectured that, when n is even, every n-by-n Latin square has a partial transversal of size n-1.[9]
A more general conjecture of Stein is that a transversal of size n-1 exists not only in Latin squares but also in any n-by-n array of n symbols, as long as each symbol appears exactly n times.[8]
Some weaker versions of these conjectures have been proved:
For small squares it is possible to generate permutations and test whether the Latin square property is met. For larger squares, Jacobson and Matthews' algorithm allows sampling from a uniform distribution over the space of n × n Latin squares.[13]
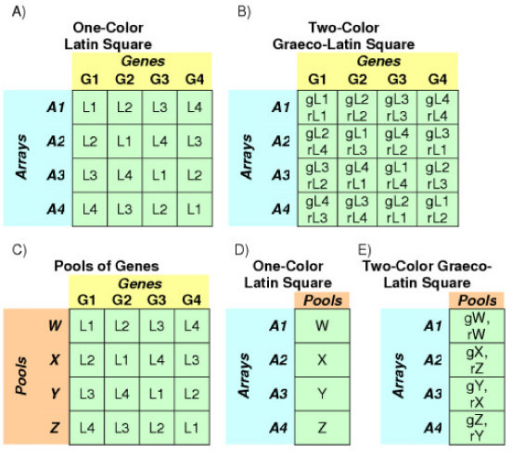
Sets of Latin squares that are orthogonal to each other have found an application as error correcting codes in situations where communication is disturbed by more types of noise than simple white noise, such as when attempting to transmit broadband Internet over powerlines.[16][17][18]
Firstly, the message is sent by using several frequencies, or channels, a common method that makes the signal less vulnerable to noise at any one specific frequency. A letter in the message to be sent is encoded by sending a series of signals at different frequencies at successive time intervals. In the example below, the letters A to L are encoded by sending signals at four different frequencies, in four time slots. The letter C, for instance, is encoded by first sending at frequency 3, then 4, 1 and 2.
The encoding of the twelve letters are formed from three Latin squares that are orthogonal to each other. Now imagine that there's added noise in channels 1 and 2 during the whole transmission. The letter A would then be picked up as:
In other words, in the first slot we receive signals from both frequency 1 and frequency 2; while the third slot has signals from frequencies 1, 2 and 3. Because of the noise, we can no longer tell if the first two slots were 1,1 or 1,2 or 2,1 or 2,2. But the 1,2 case is the only one that yields a sequence matching a letter in the above table, the letter A. Similarly, we may imagine a burst of static over all frequencies in the third slot:
Again, we are able to infer from the table of encodings that it must have been the letter A being transmitted. The number of errors this code can spot is one less than the number of time slots. It has also been proven that if the number of frequencies is a prime or a power of a prime, the orthogonal Latin squares produce error detecting codes that are as efficient as possible.
The problem of determining if a partially filled square can be completed to form a Latin square is NP-complete.[19]
The popular Sudoku puzzles are a special case of Latin squares; any solution to a Sudoku puzzle is a Latin square. Sudoku imposes the additional restriction that nine particular 3×3 adjacent subsquares must also contain the digits 1–9 (in the standard version). See also Mathematics of Sudoku.
The more recent KenKen puzzles are also examples of Latin squares.
Latin squares have been used as the basis for several board games, notably the popular abstract strategy game Kamisado.
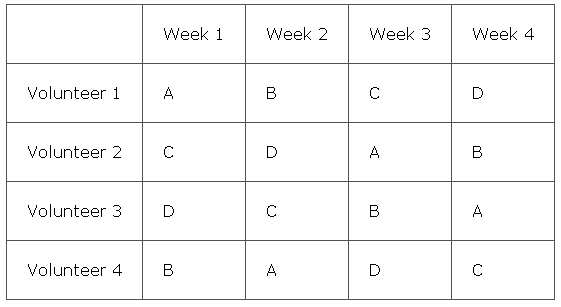
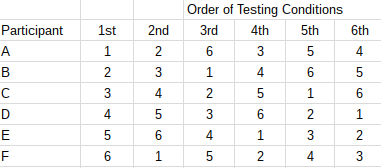
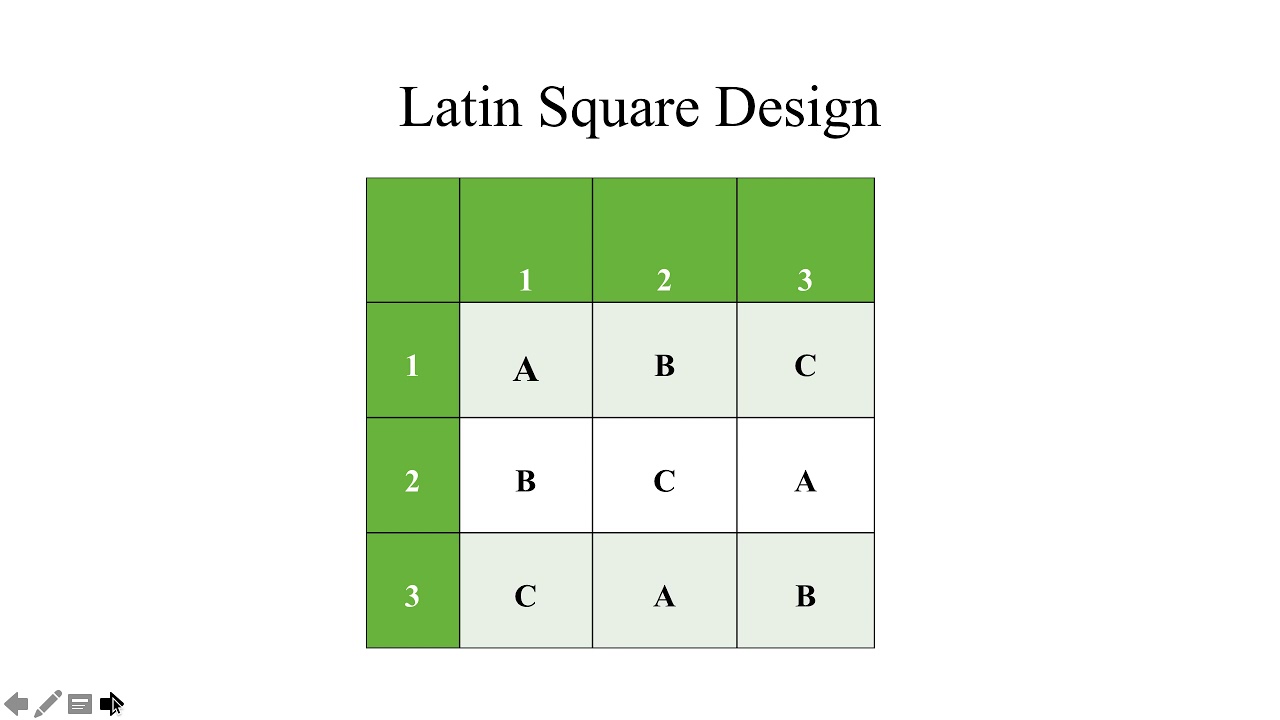
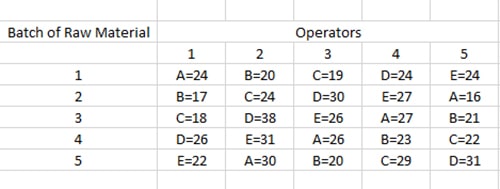
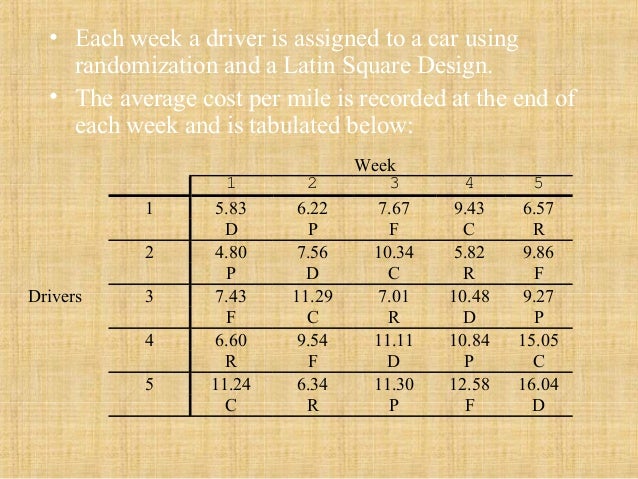
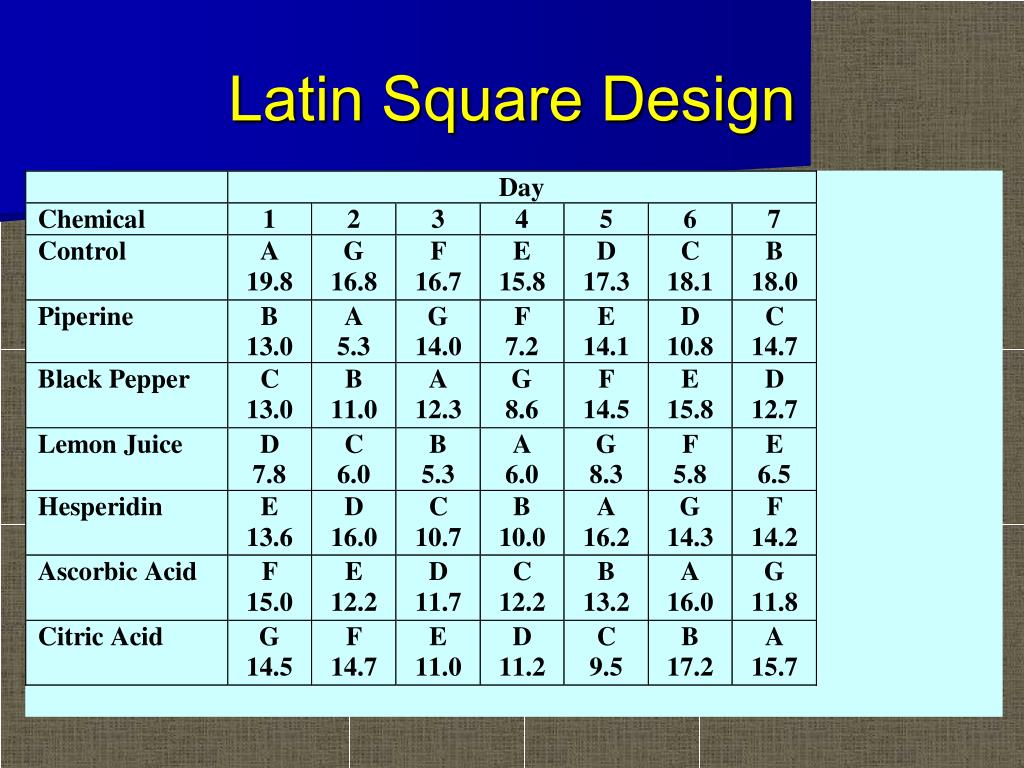
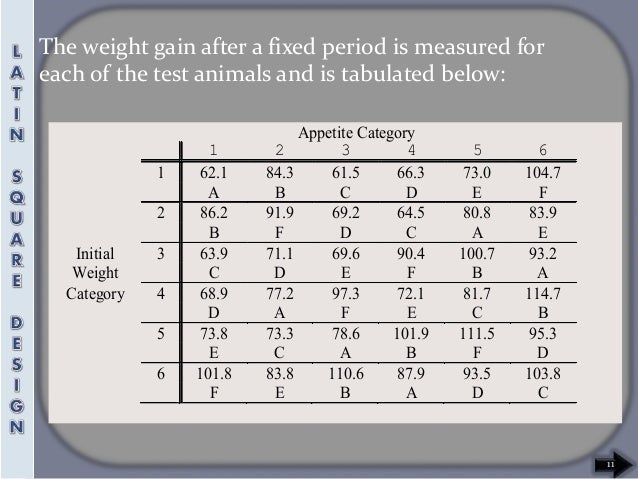
Latin squares are used in the design of agronomic research experiments to minimise experimental errors.[20]
The Latin square also figures in the arms of the Statistical Society of Canada,[21] being specifically mentioned in its blazon. Also, it appears in the logo of the International Biometric Society.[22]
^ Wallis, W. D.; George, J. C. (2011), Introduction to Combinatorics, CRC Press, p. 212, ISBN 978-1-4398-0623-4
^ Colbourn, Charles J.; Dinitz, Jeffrey H. (2 November 2006). Handbook of Combinatorial Designs (2nd ed.). CRC Press. p. 12. ISBN 9781420010541. Retrieved 28 March 2017.
^ Dénes & Keedwell 1974, p. 128
^ a b Dénes & Keedwell 1974, p. 126
^ van Lint & Wilson 1992, pp. 161-162
^ Jia-yu Shao; Wan-di Wei (1992). "A formula for the number of Latin squares". Discrete Mathematics. 110 (1–3): 293–296. doi:10.1016/0012-365x(92)90722-r.
^ Gyarfas, Andras; Sarkozy, Gabor N. (2012). "Rainbow matchings and partial transversals of Latin squares". arXiv:1208.5670 [CO math. CO].
^ a b Aharoni, Ron; Berger, Eli; Kotlar, Dani; Ziv, Ran (2017-01-04). "On a conjecture of Stein". Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg. 87 (2): 203–211. doi:10.1007/s12188-016-0160-3. ISSN 0025-5858. S2CID 119139740.
^ Stein, Sherman (1975-08-01). "Transversals of Latin squares and their generalizations". Pacific Journal of Mathematics. 59 (2): 567–575. doi:10.2140/pjm.1975.59.567. ISSN 0030-8730.
^ Koksma, Klaas K. (1969-07-01). "A lower bound for the order of a partial transversal in a latin square". Journal of Combinatorial Theory. 7 (1): 94–95. doi:10.1016/s0021-9800(69)80009-8. ISSN 0021-9800.
^ Woolbright, David E (1978-03-01). "An n × n Latin square has a transversal with at least n−n distinct symbols". Journal of Combinatorial Theory, Series A. 24 (2): 235–237. doi:10.1016/0097-3165(78)90009-2. ISSN 0097-3165.
^ Hatami, Pooya; Shor, Peter W. (2008-10-01). "A lower bound for the length of a partial transversal in a Latin square". Journal of Combinatorial Theory, Series A. 115 (7): 1103–1113. doi:10.1016/j.jcta.2008.01.002. ISSN 0097-3165.
^ Jacobson, M. T.; Matthews, P. (1996). "Generating uniformly distributed random latin squares". Journal of Combinatorial Designs. 4 (6): 405–437. doi:10.1002/(sici)1520-6610(1996)4:6<405::aid-jcd3>3.0.co;2-j.
^ Bailey, R.A. (2008), "6 Row-Column designs and 9 More about Latin squares", Design of Comparative Experiments, Cambridge University Press, ISBN 978-0-521-68357-9, MR 2422352
^ Shah, Kirti R.; Sinha, Bikas K. (1989), "4 Row-Column Designs", Theory of Optimal Designs, Lecture Notes in Statistics, 54, Springer-Verlag, pp. 66–84, ISBN 0-387-96991-8, MR 1016151
^ Colbourn, C.J.; Kløve, T.; Ling, A.C.H. (2004). "Permutation arrays for powerline communication". IEEE Trans. Inf. Theory. 50: 1289–1291. doi:10.1109/tit.2004.828150. S2CID 15920471.
^ Euler's revolution, New Scientist, 24 March 2007, pp 48–51
^ Huczynska, Sophie (2006). "Powerline communication and the 36 officers problem". Philosophical Transactions of the Royal Society A. 364 (1849): 3199–3214. doi:10.1098/rsta.2006.1885. PMID 17090455. S2CID 17662664.
^ C. Colbourn (1984). "The complexity of completing partial latin squares". Discrete Applied Mathematics. 8: 25–30. doi:10.1016/0166-218X(84)90075-1.
^ http://joas.agrif.bg.ac.rs/archive/article/59 | The application of Latin square in agronomic research
^ "Letters Patent Confering the SSC Arms". ssc.ca. Archived from the original on 2013-05-21.
^ The International Biometric Society Archived 2005-05-07 at the Wayback Machine
Content is available under CC BY-SA 3.0 unless otherwise noted.

Created, developed, and nurtured by Eric Weisstein at Wolfram Research
An Latin square is a Latin rectangle with . Specifically, a Latin square consists of sets of the numbers 1 to arranged in such a way that no orthogonal (row or column) contains the same number twice. For example, the two Latin squares of order two are given by
the 12 Latin squares of order three are given by
and two of the whopping 576 Latin squares of order 4 are given by
The numbers of Latin squares of order , 2, ... are 1, 2, 12, 576, 161280, ... (OEIS A002860). The number of isotopically distinct Latin squares of order , 2, ... are 1, 1, 1, 2, 2, 22, 564, 1676267, ... (OEIS A040082).
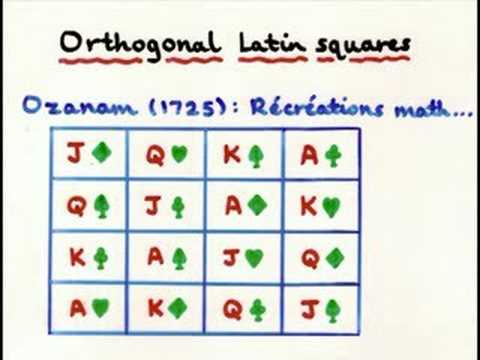
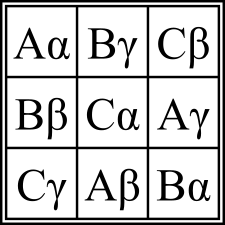
A pair of Latin squares is said to be orthogonal if the pairs formed by juxtaposing the two arrays are all distinct. For example, the two Latin squares
are orthogonal. The number of pairs of orthogonal Latin squares of order , 2, ... are 0, 0, 36, 3456, ... (OEIS A072377).
The number of Latin squares of order with first row given by is the same as the number of fixed diagonal Latin squares of order (i.e., the number of Latin squares of order having all 1s along their main diagonals). For , 2, ..., the numbers of such matrices are 1, 1, 2, 24, 1344, 1128960, ... (OEIS A000479) and the total number of Latin squares of order is equal to this number times .
A normalized, or reduced, Latin square is a Latin square with the first row and column given by . General formulas for the number of normalized Latin squares are given by Nechvatal (1981), Gessel (1987), and Shao and Wei (1992), but the asymptotic value of is not known (MacKay and Wanless 2005). The total number of Latin squares of order can then be computed from
The numbers of normalized Latin squares of order , 2, ..., are summarized in the following table (OEIS A000315).
Euler (1782), Cayley (1890), MacMahon (1915; incorrect value)
Frolov (1890; incorrect), Norton (1939; incomplete), Sade (1948), Saxena (1951)
Sudoku is a special case of a Latin square.
Bammel, S. E. and Rothstein, J. "The Number of Latin Squares." Disc. Math. 11, 93-95, 1975.
Cayley, A. "On Latin Squares." Oxford Cambridge Dublin Messenger Math. 19, 135-137, 1890.
Colbourn, C. J. and Dinitz, J. H. (Eds.). CRC Handbook of Combinatorial Designs. Boca Raton, FL: CRC Press, 1996.
Euler, L. "Recherches sur une nouvelle esp ece de quarrès magiques." Verh. Zeeuwsch Gennot. Weten Vliss 9, 85-239, 1782.
Frolov, M. "Sur les permutations carrés." J. de Math. spéc. 4, 8-11 and 25-30, 1890.
Gessel, I. "Counting Latin Rectangles." Bull. Amer. Math. Soc. 16, 79-83, 1987.
Hunter, J. A. H. and Madachy, J. S. Mathematical Diversions. New York: Dover, pp. 33-34, 1975.
Kraitchik, M. "Latin Squares." §7.11 in Mathematical Recreations. New York: W. W. Norton, p. 178, 1942.
Lindner, C. C. and Rodger, C. A. Design Theory. Boca Raton, FL: CRC Press, 1997.
MacMahon, P. A. Combinatory Analysis, Vol. 1. London: Cambridge University Press, 1915.
McKay, B. D. and Rogoyski, E. "Latin Squares of Order 10." Electronic J. Combinatorics 2, No. 1, R3, 1-4, 1995. https://www.combinatorics.org/Volume_2/Abstracts/v2i1r3.html.
McKay, B. D. and Wanless, I. M. "On the Number of Latin Squares." Ann. Combin. 9, 335-344, 2005.
Nechvatal, J. R. "Asymptotic Enumeration of Generalised Latin Rectangles." Util. Math. 20, 273-292, 1981.
Norton, H. W. "The Squares." Ann. Eugenics 9, 269-307, 1939.
Rohl, J. S. Recursion via Pascal. Cambridge, England: Cambridge University Press, pp. 162-165, 1984.
Ryser, H. J. "Latin Rectangles." §3.3 in Combinatorial Mathematics. Buffalo, NY: Math. Assoc. Amer., pp. 35-37, 1963.
Sade, A. "Enumération des carrés latins. Application au 7ème ordre. Conjectures pour les ordres supérieurs." 8 pp. Marseille, France: Privately published, 1948.
Saxena, P. N. "A Simplified Method of Enumerating Latin Squares by MacMahon's Differential Operators; II. The Latin Squares." J. Indian Soc. Agricultural Statist. 3, 24-79, 1951.
Shao, J.-Y. and Wei, W.-D. "A Formula for the Number of Latin Squares." Disc. Math. 110, 293-296, 1992.
Sloane, N. J. A. Sequences A000479, A002860/M2051, A000315/M3690, A040082, and A072377 in "The On-Line Encyclopedia of Integer Sequences."
Tarry, G. "Le problème de 36 officiers." Compte Rendu de l'Assoc. Français Avanc. Sci. Naturel 1, 122-123, 1900.
Tarry, G. "Le problème de 36 officiers." Compte Rendu de l'Assoc. Français Avanc. Sci. Naturel 2, 170-203, 1901.
Wells, M. B. "The Number of Latin Squares of Order Eight." J. Combin. Th. 3, 98-99, 1967.
The #1 tool for creating Demonstrations and anything technical.
Explore anything with the first computational knowledge engine.
Explore thousands of free applications across science, mathematics, engineering, technology, business, art, finance, social sciences, and more.
Join the initiative for modernizing math education.
Solve integrals with Wolfram|Alpha.
Walk through homework problems step-by-step from beginning to end. Hints help you try the next step on your own.
Unlimited random practice problems and answers with built-in Step-by-step solutions. Practice online or make a printable study sheet.
Collection of teaching and learning tools built by Wolfram education experts: dynamic textbook, lesson plans, widgets, interactive Demonstrations, and more.
Knowledge-based programming for everyone.

Lesbian Korean Kisses
Latin Gang
Korean Sexy Video Sqa Porno Usa
Hardest Porn Ever
Xxx Ftvgirls Viva Kinky
Latin square - Wikipedia
Latin Square -- from Wolfram MathWorld
Latin Square - an overview | ScienceDirect Topics
Combinatorial Designs: Latin Squares
Latin Squares in Experimental Design - CompNeurosci
Latin Square - GeeksforGeeks
Mutually orthogonal Latin squares - Wikipedia
Latin Squares Design | Real Statistics Using Excel
Latin Square