LNN Часть 2. Closed-form continuous time RNN

Update:

Тетрадка с реализацией CfC с нуля в Telegram-канале "То шо нейросети"

В прошлый раз я описал принцип устройства Liquid Time-Constant RNN и сделал тетрадку с разбором.

У LTC есть очевидный недостаток: зависимость от ODE Solver'а, который считать дорого. Авторы решили устранить этот недостаток, проанализировали динамику и пришли к closed-form решению для определения состояния Leaky Integrate Fire нейрона в любой момент времени. Решение неточное, но тесно ограничено сверху и снизу по отношению к честному ODE Solver расчету. Динамику повторяет, и ладушки.

Итак, сама статья.

Как выглядит уравнение динамики нейрона в классической LTC:

Его проанализировали, выдвинули и доказали пару теорем и получили closed-form решение:

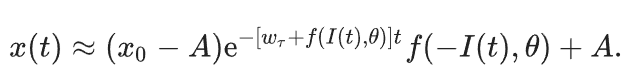
Дальше обобщают уравнение (2) для общего случая многомерных входных последовательностей:

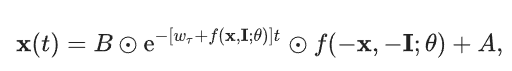
Экспоненциальный член в уравнении (3) заставляет первую часть системы (экспоненциально быстро) стремиться к нулю и весь скрытый слой стремится к A. Эта проблема становится более очевидной, когда присутствуют рекуррентные связи, и вызывает факторы исчезновения градиента при обучении методом градиентного спуска. Чтобы уменьшить этот эффект, авторы заменяют член экспоненциального затухания на обратную сигмоидальную нелинейность σ(.). Эта нелинейность приблизительно равна 1 при t = 0 и стремится к 0 в пределе t → ∞. Однако, в отличие от экспоненциального затухания, её переход происходит гораздо более плавно, что обеспечивает лучшее состояние на поверхности потерь.

Далее, авторы рассматривают параметр смещения B как часть обучаемых параметров нейронной сети f( − x, − I; θ) и используют новый экземпляр сети вместо f (представленной в факторе экспоненциального затухания). Также заменяют A на другой экземпляр нейронной сети, h(. ), чтобы повысить гибкость модели. Для получения более общей архитектуры сети авторы допускают, что нелинейность f(−x, −I; θ), представленная в уравнении (3), имеет как общие (основные), так и независимые (g(. )) компоненты сети.

Временной сигмоидальный член может играть роль гейта, если мы дополнительно умножим h(. ) на (1 − σ(. )). Таким образом, временная сигмоидальная функция представляет собой механизм гейта, который интерполирует между двумя пределами t → −∞ и t → ∞ траектории ОДУ.

Вместо обучения всех трех экземпляров нейронных сетей f, g и h отдельно, авторы предлагают сделать так, чтобы все сети имели общие первые несколько слоев в форме основного блока, который разветвляется на эти три функции. В результате основной блок позволяет нашей модели обучаться на общих представлениях, тем самым ускоряя и стабилизируя процесс обучения. Это архитектурное решение обеспечивает два одновременных преимущества: (1) Через общий основной блок устанавливается связь между временной константой системы и её нелинейностью состояния, что использует каузальное обучение представлений (2) через отдельные слои головной сети система имеет возможность изучать временные и структурные зависимости независимо друг от друга.

Эти модификации приводят к модели нейронной сети CfC:

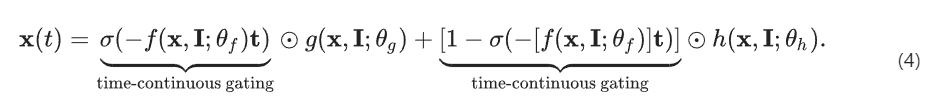
Таким образом авторы получают модель с непрерывной глубиной, которая может настраивать свое временное поведение в зависимости от задачи, проходящей тестирование. Для временно-зависимых наборов данных (например, нерегулярно отслеживаемых временных рядов, событийных данных и разреженных данных) параметр t для каждой входящей выборки устанавливается на основе её временной метки или порядка. Для последовательных приложений, где время возникновения выборки не имеет значения, t выбирается столько раз, сколько длина батча, с равными интервалами в пределах выбранного диапазона.

Вот собственно и все. Дальше авторы статьи приводят серию исследований производительности сети на разных задачах.

Тетрадка с реализацией CfC с нуля в Telegram-канале "То шо нейросети"

Вы великолепны!