L₂ и L₁ нормы вектора

Вектор — это направленный отрезок, и для действий с ним хорошо бы знать его длину. В линейной алгебре длину вектора называют нормой. Норм у вектора несколько, и все они вычисляются разными способами, давая на выходе разные значения.

Сегодня мы расскажем про две нормы, которые часто применяют в анализе данных и Data Science. Поясним, как их вычислять и зачем они нужны.

Для примера возьмём вот такой вектор OK:

Норма L₂

Способ первый: считаем норму как расстояние от начала до конца вектора. На иллюстрации к посту это расстояние между точкой O и точкой K. В идеальном мире мы идём от одной точки к другой по прямой, и расстояние между точками равно кратчайшему расстоянию между ними.

Посчитать его можно по теореме Пифагора.

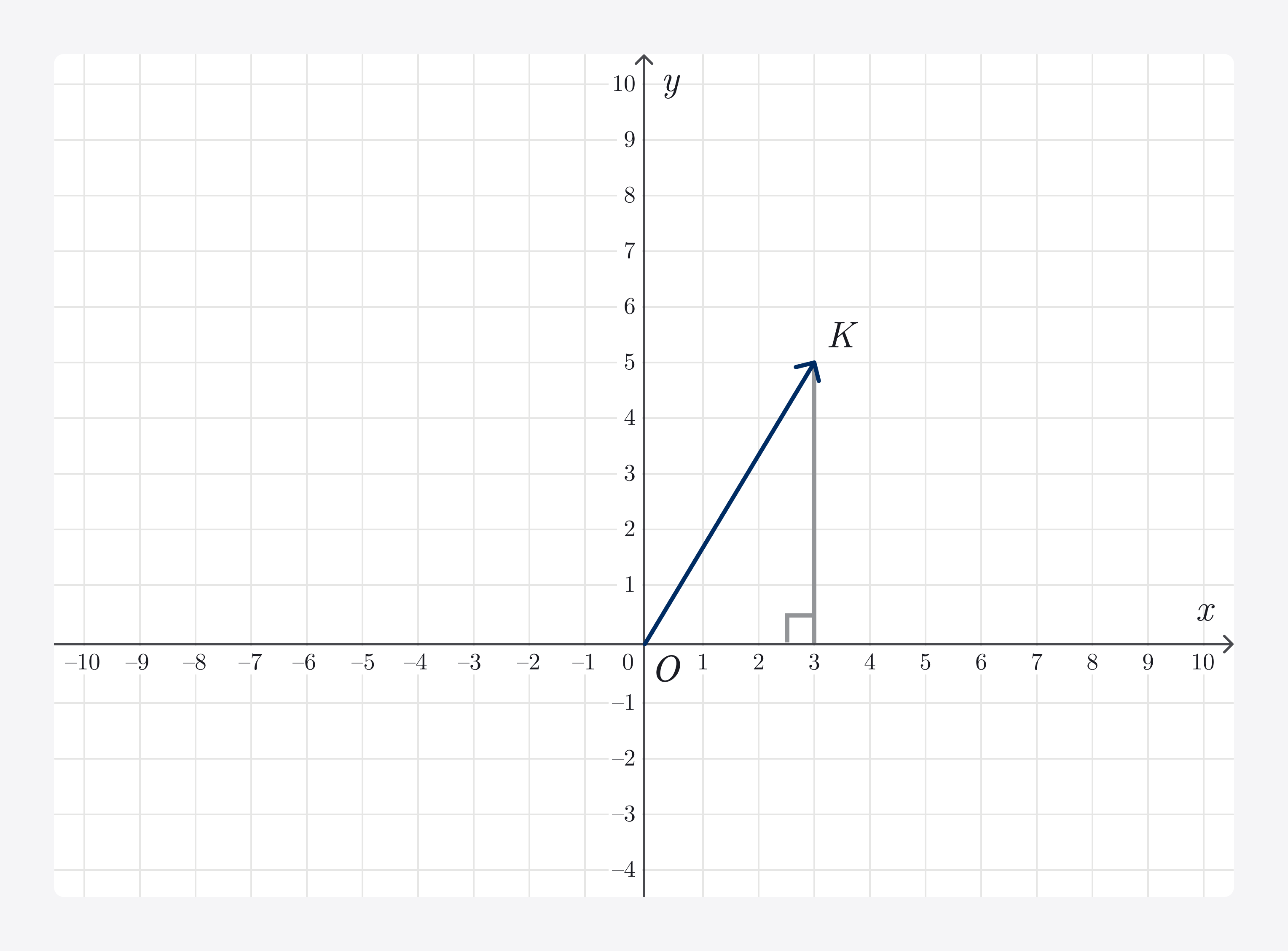
Наш вектор — это гипотенуза, и квадрат его нормы равен сумме квадратов катетов: |OK|² = 3²+5² = 34, отсюда |OK|≈5.8.

Такую норму называют евклидовой, или нормой L₂ (нижний индекс 2 показывает, что при расчёте использованы квадраты). Квадрат этой нормы равен сумме квадратов координат.

В многомерном случае это выглядит так:

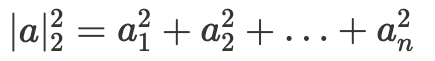
И отсюда:

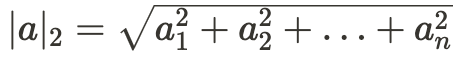
Эта норма — самая распространённая, поэтому если внизу не написан никакой индекс, то речь именно о ней. Но для однозначности лучше указывать индекс 2.

Норма L₁

Переместимся в реальный мир. Увы, длина фактического пути от одной точки до другой не всегда равна наименьшему расстоянию. 800 метров птичьего полёта от остановки до дома превращаются в путь длиной 1.5 км из-за зданий, рек, расположения пешеходных переходов и прочего.

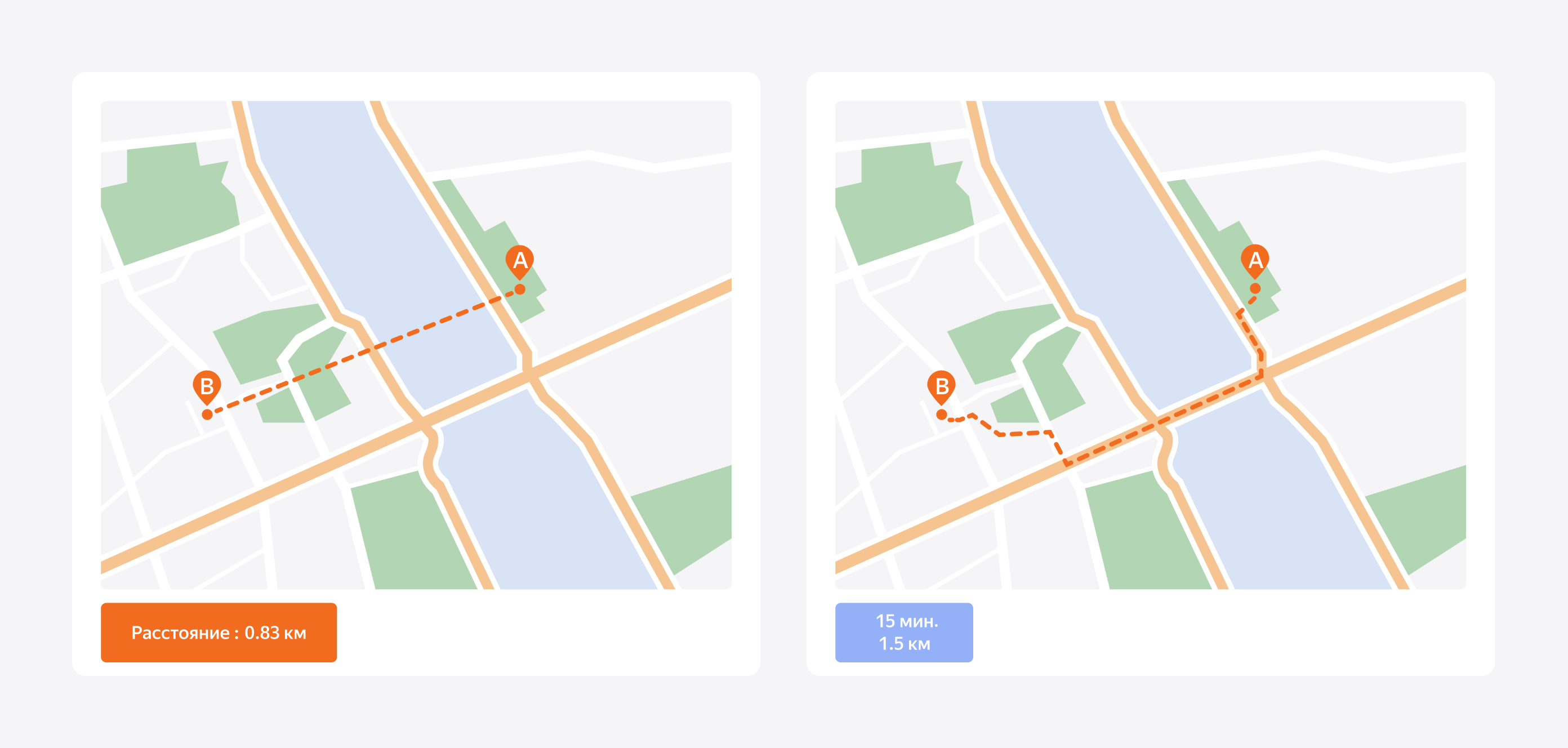
Если все обходы препятствий мы будем совершать под прямым углом, а потом просуммируем длины отрезков, то получим норму L₁ (нижний индекс 1 показывает, что длины берутся в 1 степени, то есть сами по себе).

У этой нормы много названий: прямоугольная метрика, метрика прямого угла, метрика городского квартала, норма такси, метрика Манхэттена. Последние варианты связаны с реальной географией: улицы Манхэттена в Нью-Йорке образуют прямоугольную сетку, поэтому длина пути от одной точки до другой — это сумма отрезков, расположенных под прямым углом друг к другу.

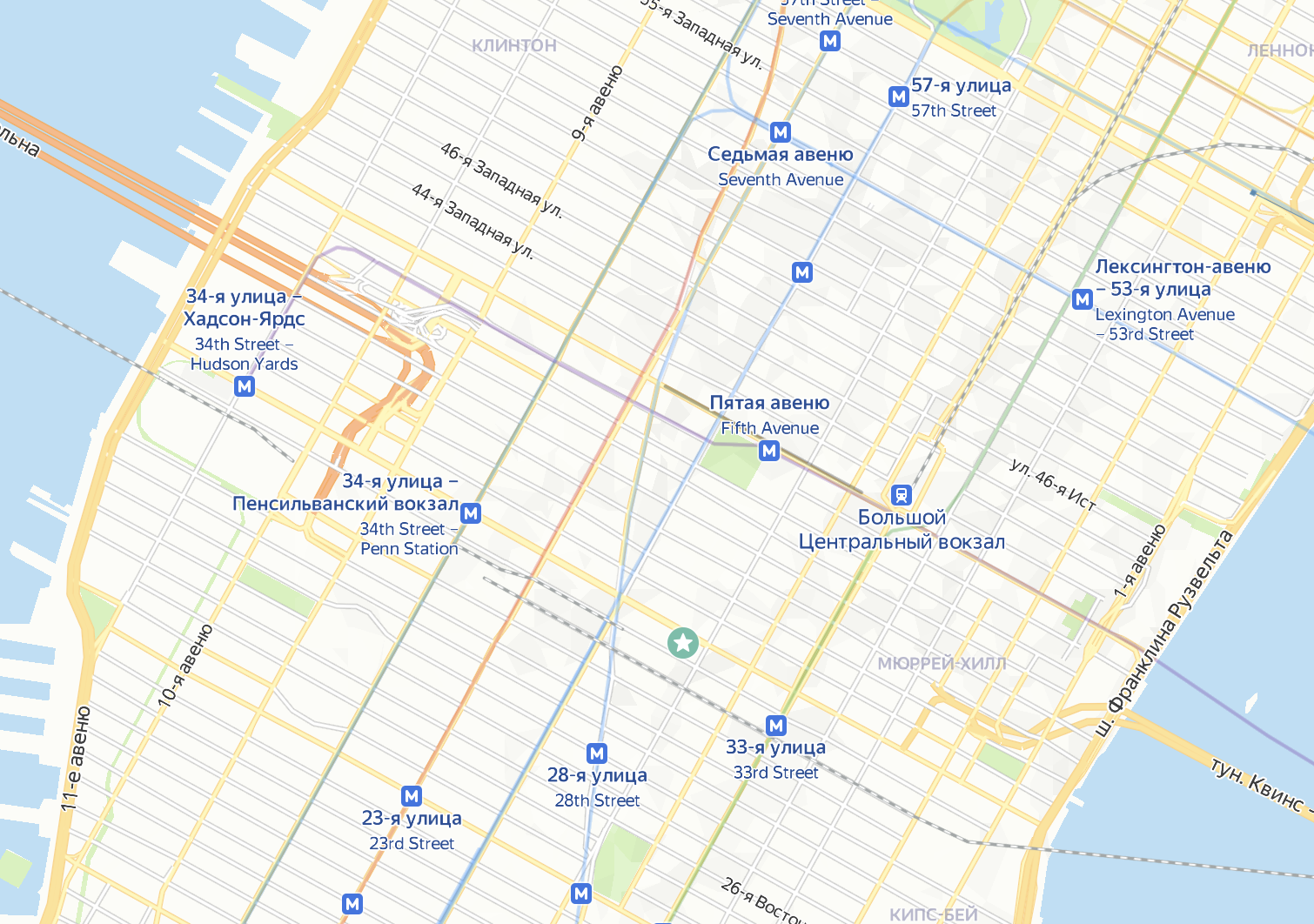
Запустим такси по нашей координатной плоскости. Каждая клетка — это один квартал. От начала координат до точки K можно «доехать» разными способами:

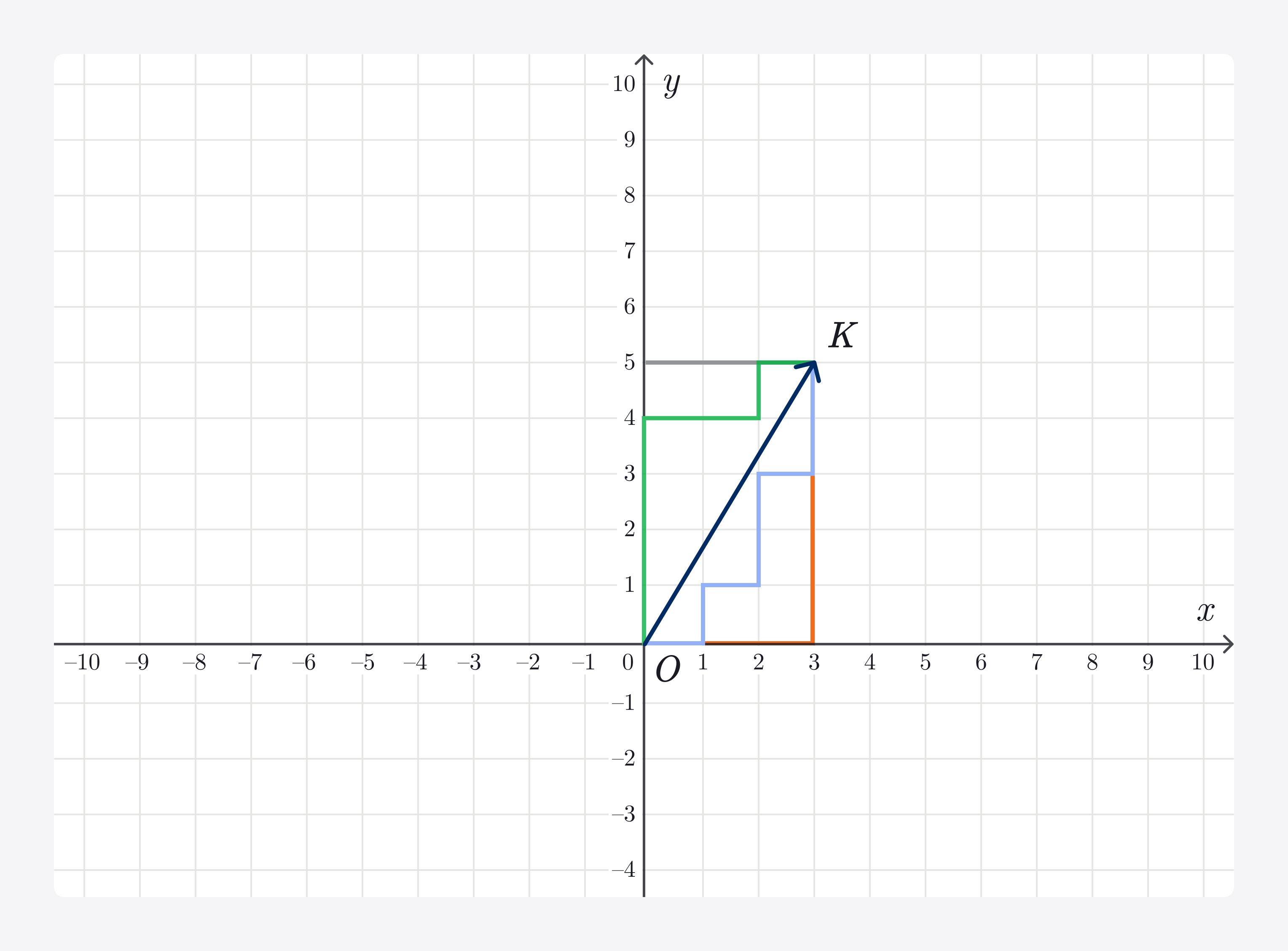
В любом случае такси проедет 3 клетки вправо и 5 клеток вверх. L₁ норма равна сумме модулей координат.

В многомерном случае:

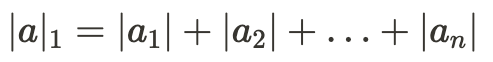
Итого две нормы для нашего вектора OK имеют такие значения:

Евклидова — 5.83, норма такси — 8.

Выбираем норму

Какую норму использовать — зависит от ситуации. Основная задача любой нормы — дать представление о размере вектора и возможность сравнить два вектора между собой. А дальше вопрос уже в том, как именно мы хотим сравнивать и какие характеристики нам более важны.

Чаще всего применяют L₂ норму. В школьной математике ею и ограничиваются. Но за счёт того, что в этой норме содержатся квадраты координат, на неё большое влияние оказывают именно большие координаты. Возведение в квадрат увеличивает их ещё сильнее и в общей сумме они становятся ещё значимее.

В норме L₁ мы просто берём модули от координат, и все координаты равномерно влияют на результат.

Представим, что мы покупаем у разных поставщиков стройматериалы и сравниваем векторы цен: у кого-то цена на краску ниже, а на кирпич — выше, а у другого — наоборот. Прайс-лист конкретного поставщика — это вектор.

Если мы планируем покупать материалы разной ценовой категории, то сравнить прайс-листы поможет норма L₁. Для нас неважно, какой именно материал дешевле — важнее понять, что в общем и целом вот этот поставщик выгоднее.

Если же мы планируем больше закупаться дорогими материалами, то стоит опираться на норму L₂. Так как в неё входят квадраты, то рост цен именно на самые дорогие товары повлияет на неё сильнее.

Пример

Посмотрим на примере:

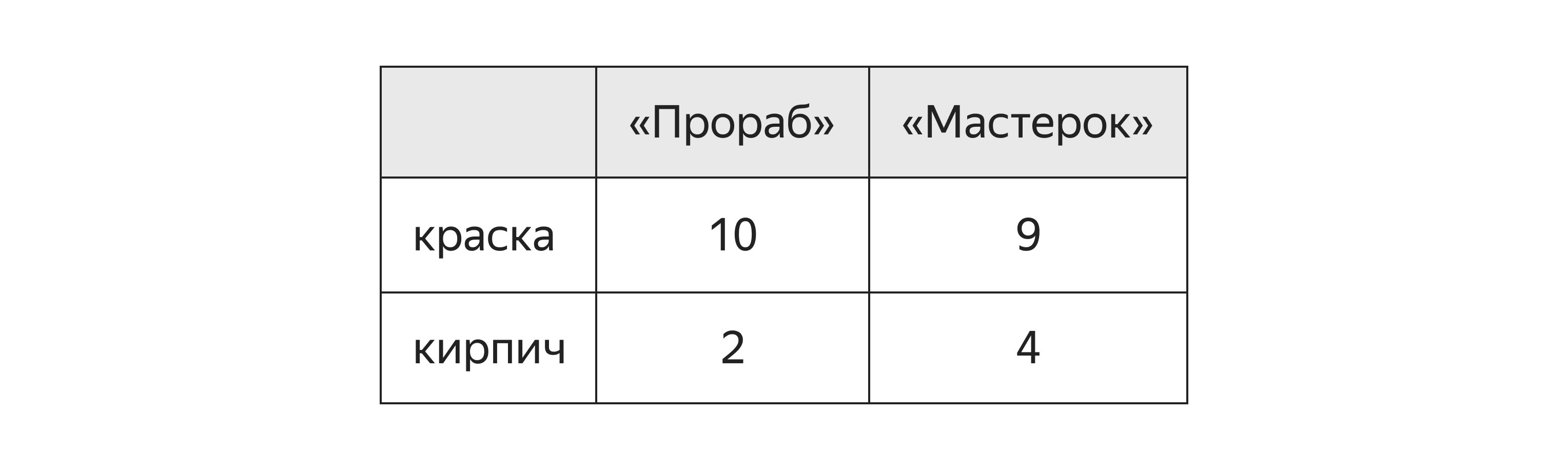
Норма L₁ для «Прораба» равна 12, а для «Мастерка» — 13. Значит, если мы планируем покупать примерно одинаково краски и кирпича, то стоит заключать контракт с «Прорабом».

Норма L₂ для «Прораба» равна корню из 10²+2², что примерно 10.2. А для «Мастерка» норма L₂ равна корню из 9²+4², что примерно 9.85. Значит, если мы закупаем больше краски, то стоит сотрудничать с «Мастерком». Сейчас этот вывод может показаться очевидным и без высчитывания норм, но для многомерных случаев и больших реальных прайс-листов удобно иметь формулы. 😇

Обратите внимание, что цена на краску у «Мастерка» ниже всего на 1 единицу, а на кирпич — выше на целых 2. Но на норму L₂ большее влияние оказывают именно крупные значения.

Ещё пример

Другой пример — в большой компании одному из бизнес-юнитов урезали бюджет. Теперь нужно оптимизировать внутренние проекты. Кое-где закрыть недорогие эксперименты, а где-то и снижать финансирование на крупные проекты. Здесь норма L₁ поможет сравнить эффект от разных вариантов.

Разобраться с другими нормами и их применением, а также научиться реализовывать алгоритмы с ними на Python можно на курсе «Математика для анализа данных».