Квадратный корень

Мы остановились на том, что древние греки, нарисовали на песке квадрат (они любили всякие красивые штуки рисовать) со стороной равной единице (длина стороны квадрата равна какой-то мере длины - отрезку –эталону, которую использовали греки). Посмотрели на этот квадрат, сообразили, что НЕВОЗМОЖНО сторону квадрата – единичный отрезок поделить на КОНЕЧНОЕ число РАВНЫХ по длине отрезков поменьше, а потом ЦЕЛОЕ число таких отрезков уложить на диагональ этого квадрата так, чтобы они точь в точь накрыли диагональ.

Для самых сообразительных, в частности для моего друга доктора наук «С» (он сразу сообщит, что кусочков не хватит, т.к. диагональ квадрата больше его стороны), заметим, если не хватит накрыть диагональ кусочками, получившимися после разрезания одного единичного отрезка, то разрешается ровно таким же способом разрезать второй единичный отрезок и взять сколько  надо маленьких отрезков  из получившейся кучи. И даже в этом случае (сейчас кусочков должно хватить)   уложить целое число отрезков не получится, как бы мелко мы не резали.

Как математика решила эту проблему? Итак, требуется решить уравнение (Рис.1):

Для всех ОТРИЦАТЕЛЬНЫХ значений a уравнение НЕ ИМЕЕТ решений (Рис.2). 

Действительно, правила умножения отрицательных чисел – это неотъемлемая часть понятия отрицательных чисел. Результат умножения двух чисел является отрицательным числом только тогда, когда перемножаемые числа - разных знаков. Тут имеет смысл немного поумничать и заявить, что правило, сообщающее, что отрицательное число, умноженное на отрицательное число – есть положительное число – это ДОГОВОРЕННОСТЬ. Оправдывая эту договоренность, скажем, что никак иначе договориться было невозможно. Комплексные числа, изобретенные много позже отрицательных, показали, насколько красиво «работает» такая договоренность. Комплексные числа рассмотрим позже, завершая тему эволюции числа в школьной программе.

Вернемся к уравнению. Итак, когда в правой части отрицательное число, уравнение не имеет решений - решением уравнения является пустое множество. (Умножив на себя любое число никогда не получим отрицательное, а нам нужно ОТРИЦАТЕЛЬНОЕ, чтобы указать корни уравнения).

Рассмотрим случай, когда в правой части ноль. Также все понятно: решением уравнения является число ноль, других решений нет (Рис.3).

Решим уравнение (Рис.4):

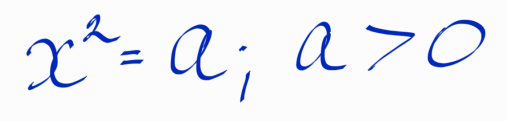
Доказали, что используя только рациональные числа, записать решения НЕВОЗМОЖНО. 

ИЗОБРЕТАЕМ новый математический объект.

Построим на одной координатной плоскости графики функций, левой и правой части уравнения (Рис.5):

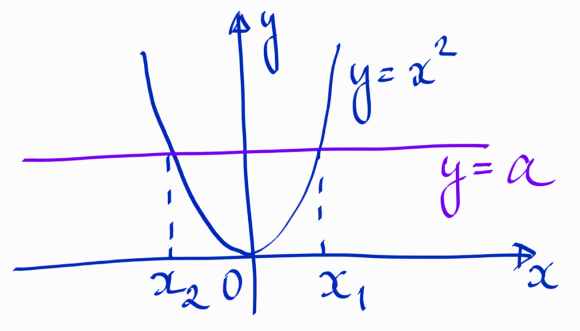
Ясно, что для любого ПОЛОЖИТЕЛЬНОГО значения a, графики ВСЕГДА пересекаются в ДВУХ точках и возможно допустить, что математика могла бы договориться так (Рис.6):

Здесь треугольник указывает, что сконструированные символы - есть ДВА корня  уравнения, такого, что в его в левой части – квадрат неизвестной, в правой – постоянная величина, символ внутри треугольника указывает как именно выглядит эта постоянная величина в правой части, а направление треугольника вершиной вверх или вниз  указывает какой корень записан - ПОЛОЖИТЕЛЬНЫЙ или ОТРИЦАТЕЛЬНЫЙ.

Математику такая договоренность не устроила, математика уже изобрела отрицательные числа.   Расстояния от абсцисс точек пересечения (проекций точек пересечения на ось x) до начала координат РАВНЫ, тогда собственное обозначение для отрицательного корня оказывается излишним (Рис.7): 

Осталось осознать грандиозную дороговизну и бесполезность кампании по переименованию КВАДРАТНОГО КОРНЯ в треугольник с вершиной вверху, ПОНЯТЬ и принять договоренность:

Назовем квадратным корнем из a НЕОТРИЦАТЕЛЬНОЕ решение уравнения (Рис.8): 

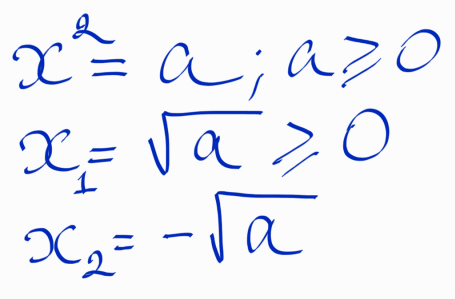
В следующем соображении обсудим правила работы с квадратным корнем и типичные ошибки. Будет интересно!