Конструктивная онтология
sergey shishkin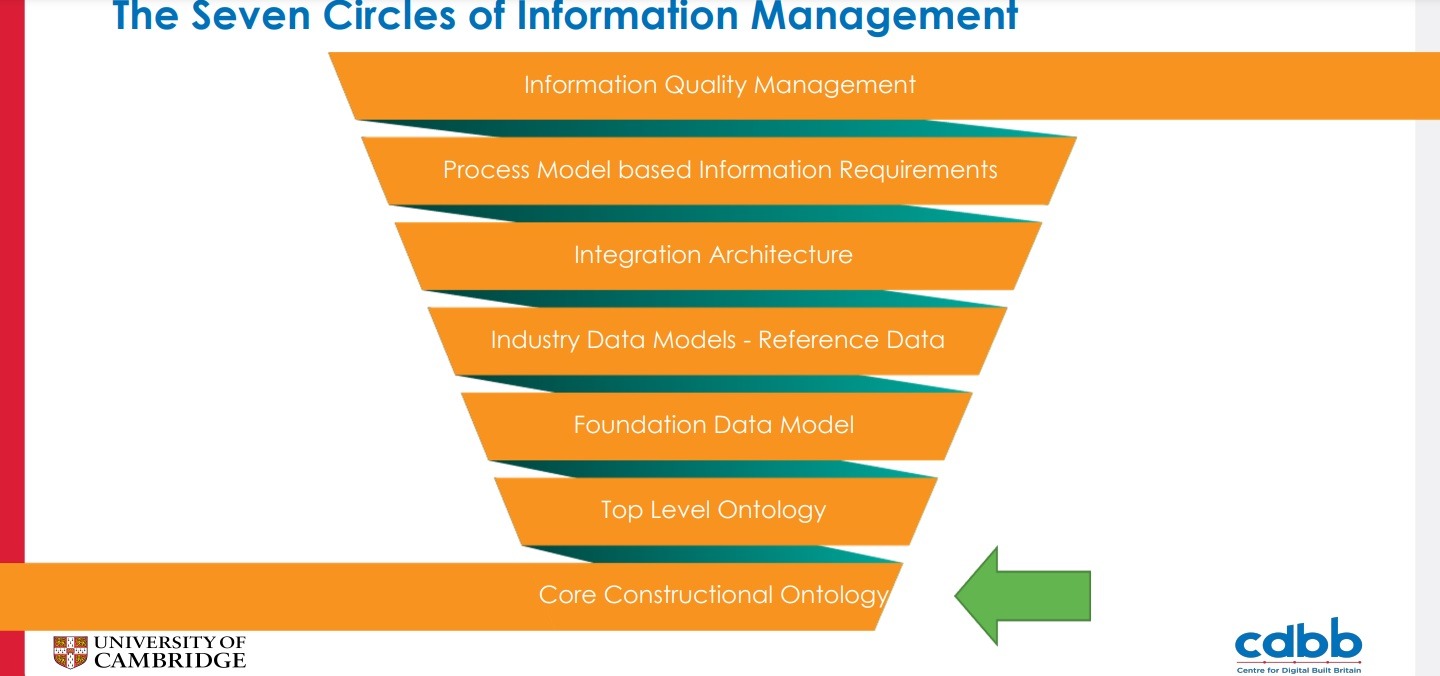
План
- Constructional ontology: background
- Our approach
- Key features of the approach
- Overview of the formalisation
Disclaimer
- Reporting on the current state of our work
- First attempt
- MVP approach
- We expect to improve and extend our approach in future work.
3. Feedback welcome!
Constructional ontology: background
Constructional ontology: the basic idea
- Start with some objects (“givens”) or even an empty domain.
- Construct the rest of the ontology by applying selected constructors.
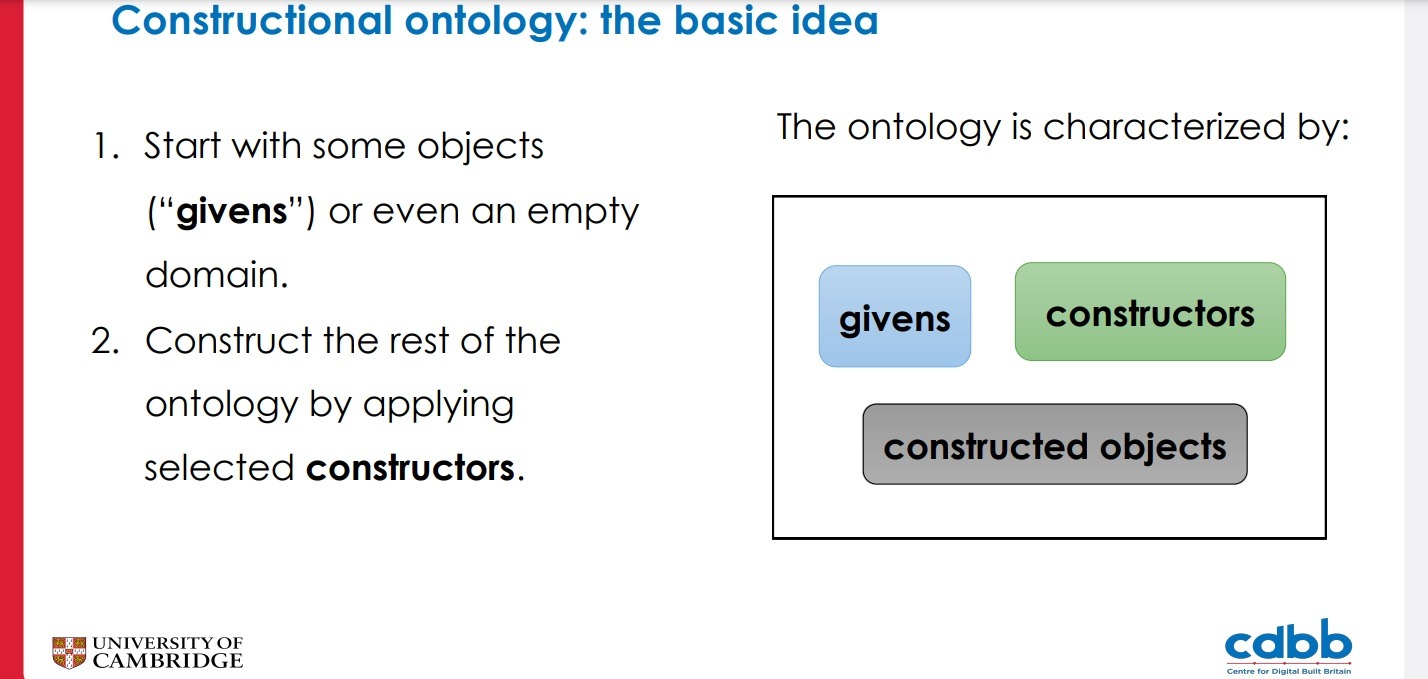
- Generally, the types of objects are determined by the constructors that generated the objects.
- The identity of constructed objects is dictated by their constructors and the inputs of the constructions.
Gödel on a concept of set
“The concept of set […] according to which a set is anything obtainable from the integers (or some other well-defined objects) by iterated application of the operation ‘set of’[…]” (Gödel, What is Cantor's continuum problem?)
Recent work
This framework has been recently advocated by Kit Fine. We build on his ideas

All use subject to https://about.jstor.org/terms c. c
TOWARDS A THEORY OF PART* My aim in this paper is to outline a general framework for dealing with questions of part-whole. Familiar as this topic may be, my treatment of it is very different from more conventional approaches. For instead of dealing with the single notion of mereological part or sum, I have attempted to provide a comprehensive and unified account of the different ways in which one object can be a part of another. Thus mereology, as it is usually conceived, becomes a small branch of a much larger subject. My discussion has been intentionally restricted in a number of ways. In the first place, my principal concern has been with the notion of absolute rather than relative part. We may talk of one object being a part of another relative to a time or circumstances (as when we say that the tire was once a part of the car or that the execution of Marie Antoinette was as a matter of contingent fact a part of the French Revolution) or in a way that is not relative to a time or the circumstances (as when we say that this pint of milk is a part of the quart or that the letter ‘c’ is part of the word ‘cat’). Many philosophers have supposed that the two notions are broadly analogous and that what goes for one will tend to go for the other.1 I believe this view to be mistaken and a source of endless error. But it is not my aim to discuss either the notion of relative part or its connection with the absolute notion.2 * The material outlined in this paper has been developed over a period of thirty years. It was most recently presented in a seminar at Princeton in 2000; and I am grateful to Cian Dorr, Michael Fara, Gail Harman, Mark Johnston, David Lewis, and Gideon Rosen for their comments. I am also grateful for some comments I received from Ted Sider and two anonymous referees for this journal; and I owe a special debt of thanks to Achille Varzi for his encouragement. 1 As in Ted Sider, Four Dimensionalism (New York: Oxford, 2001), for example. 2 The matter is briefly discussed in Kit Fine, “Things and Their Parts,” Midwest Studies in Philosophy, xxiii (1999): 61–74. 0022-362X/10/0711/559–589 ã 2010 The Journal of Philosophy, Inc. 559
Our approach
Core Constructional Ontology (CCO): our current approach
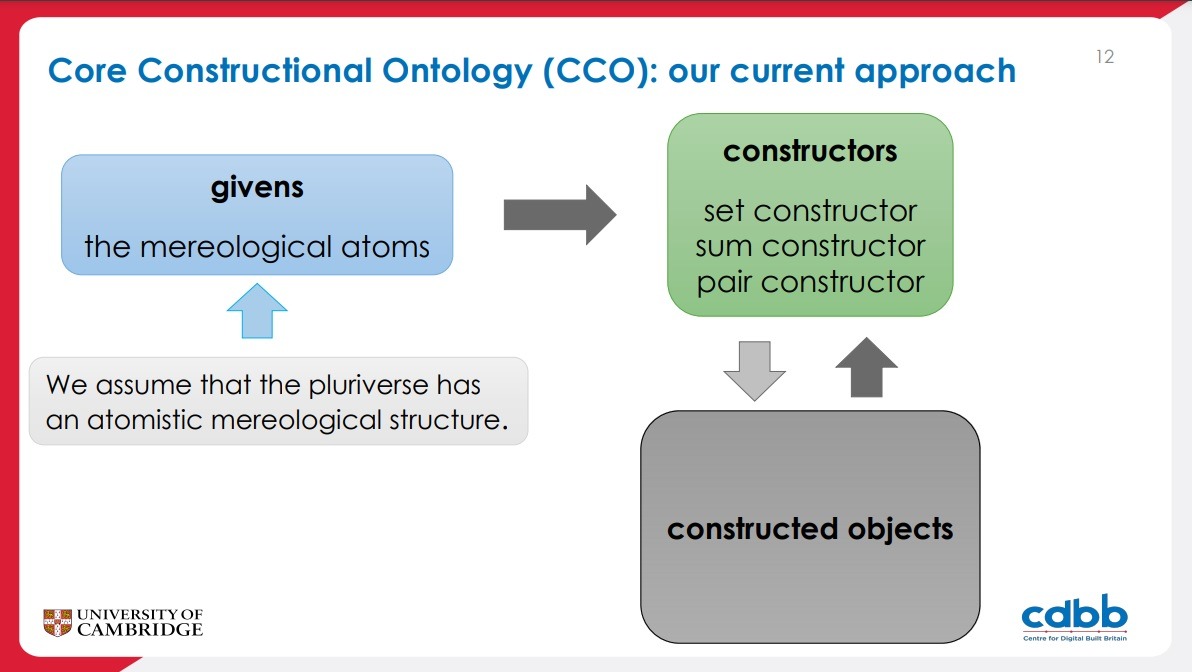
Key features and benefits of the approach
- Foundational
- Unifying
- Constructional
Foundational
Object completeness
The construction process (“object factory”) supplies all the objects needed (resulting in an “object store”).
Categorical completeness
The approach also supplies the three basic types of objects (sets, parts, and tuples) together with their associated hierarchical relations.
Identity criteria
The construction determines the conditions for the identity of constructed objects (extensional based on the type of constructor and its input).
Unifying
Common development of three domains (sets, parts, and tuples)
Three “domains” (sets, parts, tuples) arising in similar ways, i.e. through construction. Common basis for identity criteria
Identity criteria for objects of the basic types are extensional, with differences arising from the way they are constructed.
Uniform way of capturing key commonalities and differences
Commonalities and differences between objects of the basic types can be captured by features of the underlying constructors.
Constructional
Categorical differences are constructional differences
The ways of construction are the basis for differences in kinds of objects.
Dependency
Some objects are built from other objects and hence “depend on” them.
Reduction
The ontology is built out of a relatively small set of fundamental objects.
Consistency
Construction can be a basis for consistency
Consistency
“The concept of set […] according to which a set is anything obtainable from the integers (or some other well-defined objects) by iterated application of the operation ‘set of’, […] has never led to any antinomy whatsoever; that is, the perfectly ‘naïve’ and uncritical working with this concept of set has so far proved completely self-consistent.” (Gödel, What is Cantor's continuum problem?)
Core Constructional Ontology and 4-dimensionalism
Core Constructional Ontology supplies the required types:
Process Model based Information Requirements ?
- sets
- sums
- tuples
with the required extensional criteria of identity.
Formalising the Core Constructional Ontology

A number of options are available.
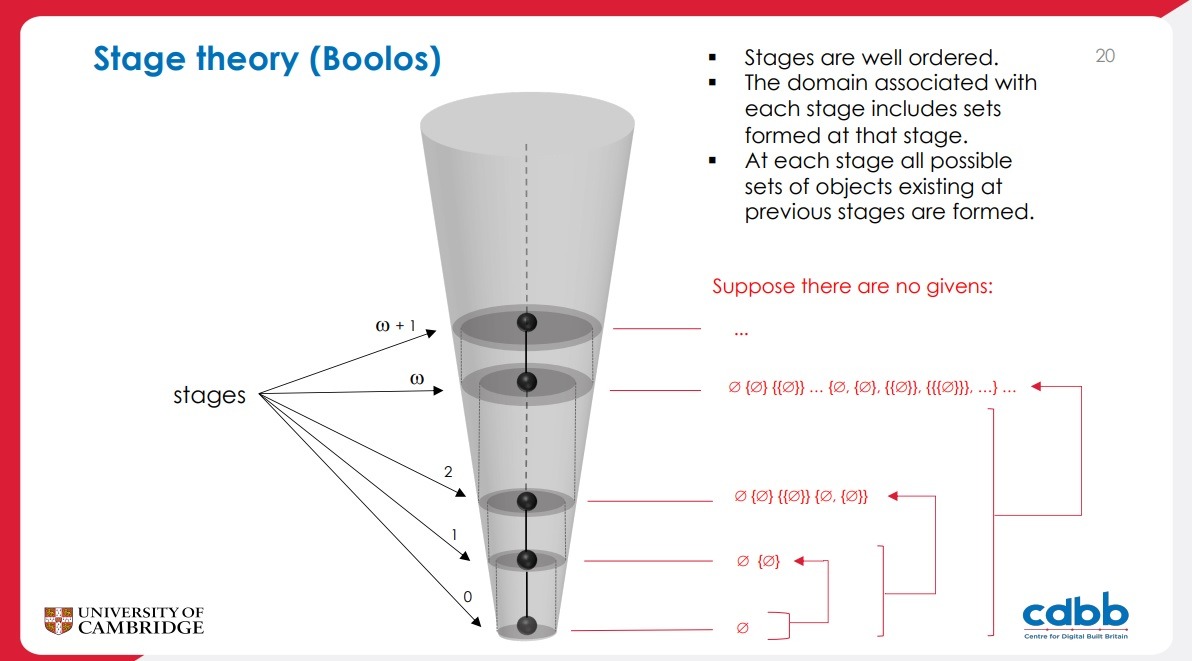
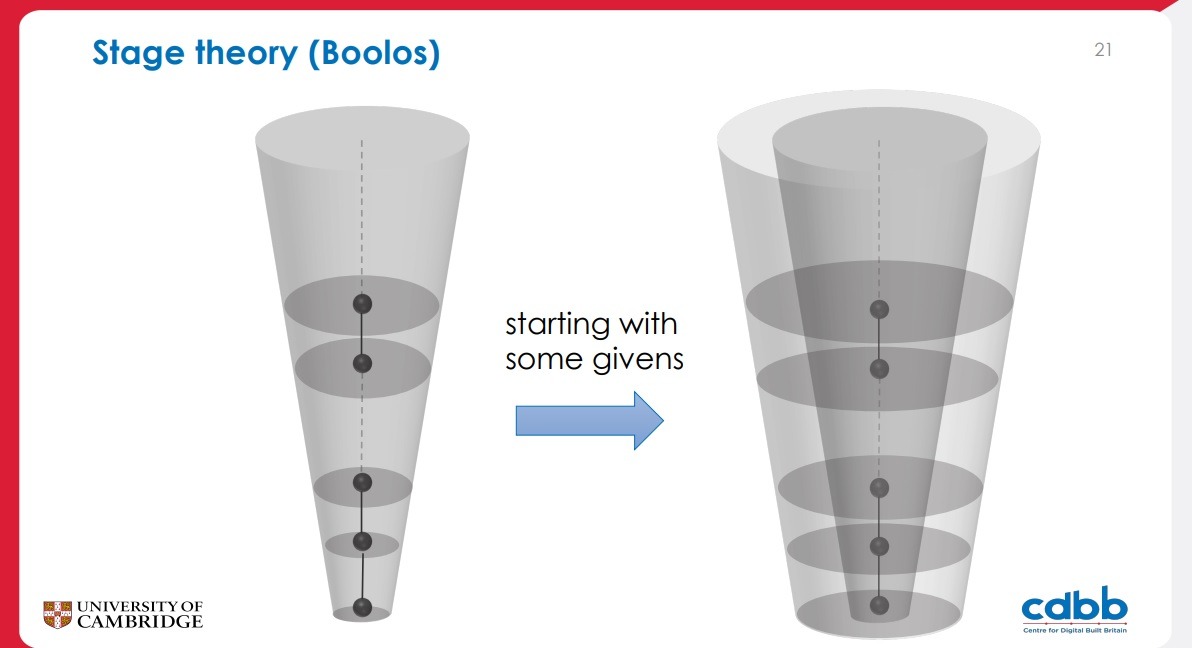
For this early phase, we chose a stage theory, inspired by
- Gödel’s remark;
- George Boolos’s development of the iterative conception of set based on a stage theory
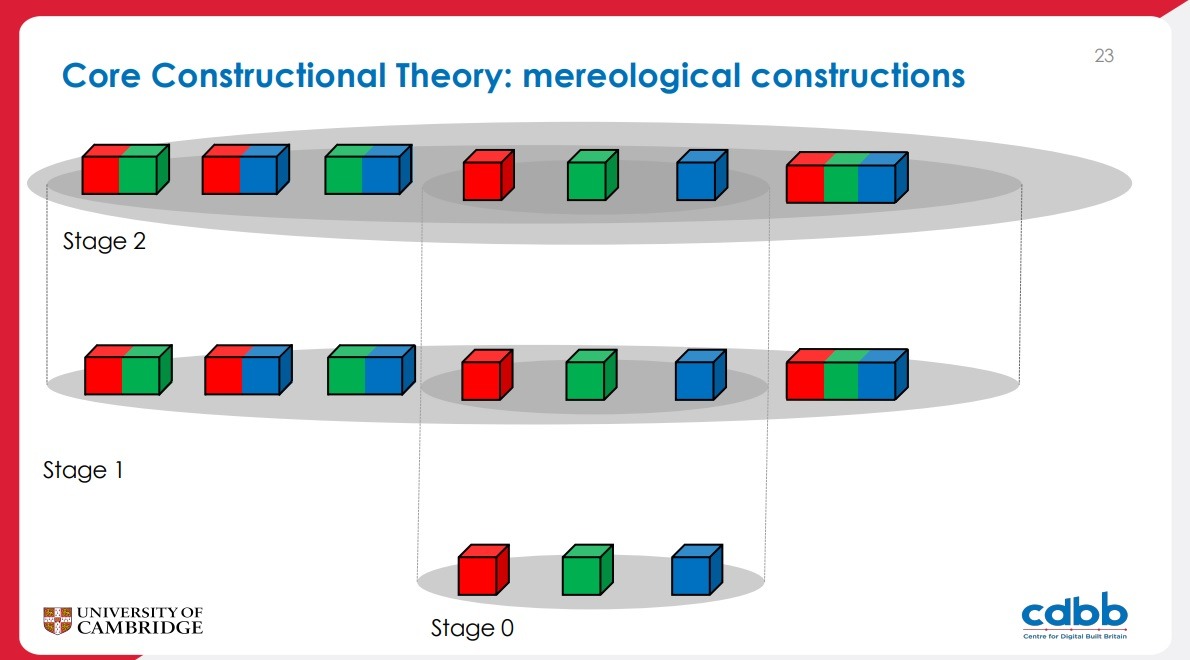
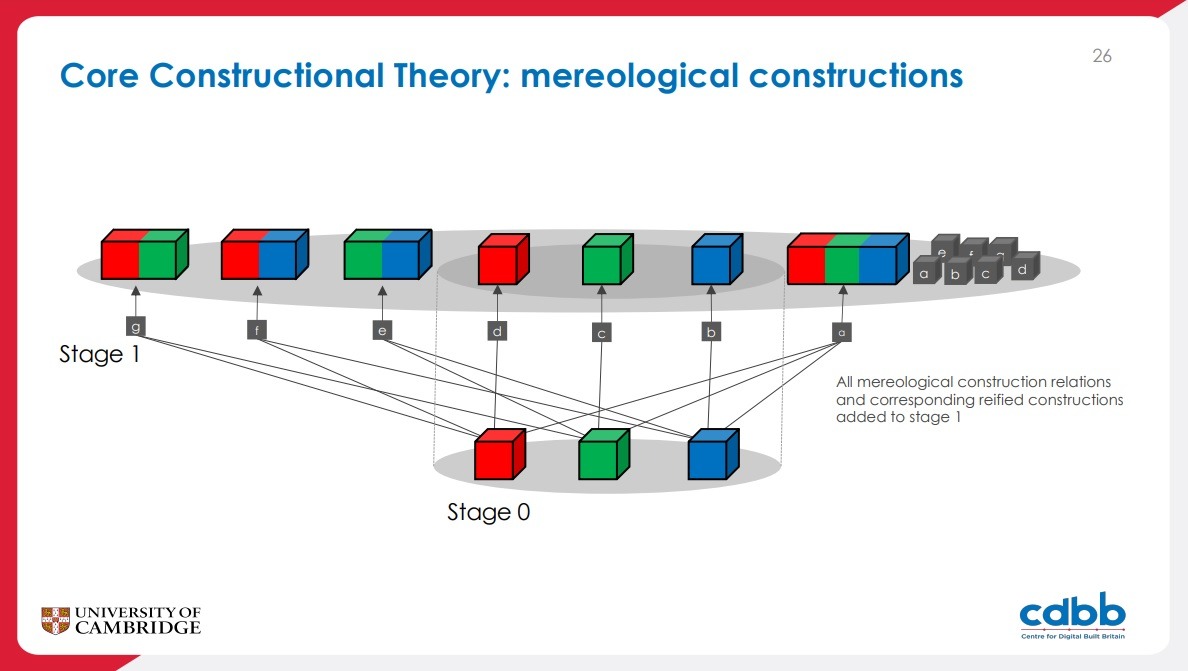
Core Constructional Theory: novelty
Our work generalizes and extends Boolos’s stage theory in three main ways:
- we provide a unified account of parts, sets, and tuples;
- we allow a more flexibile construction process;
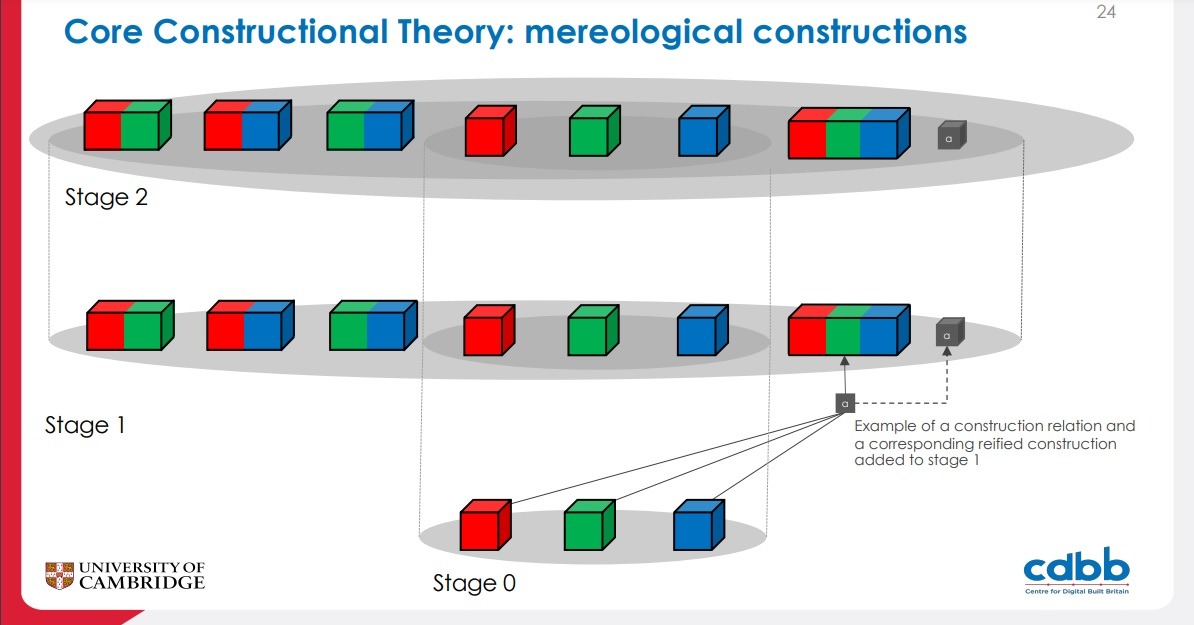
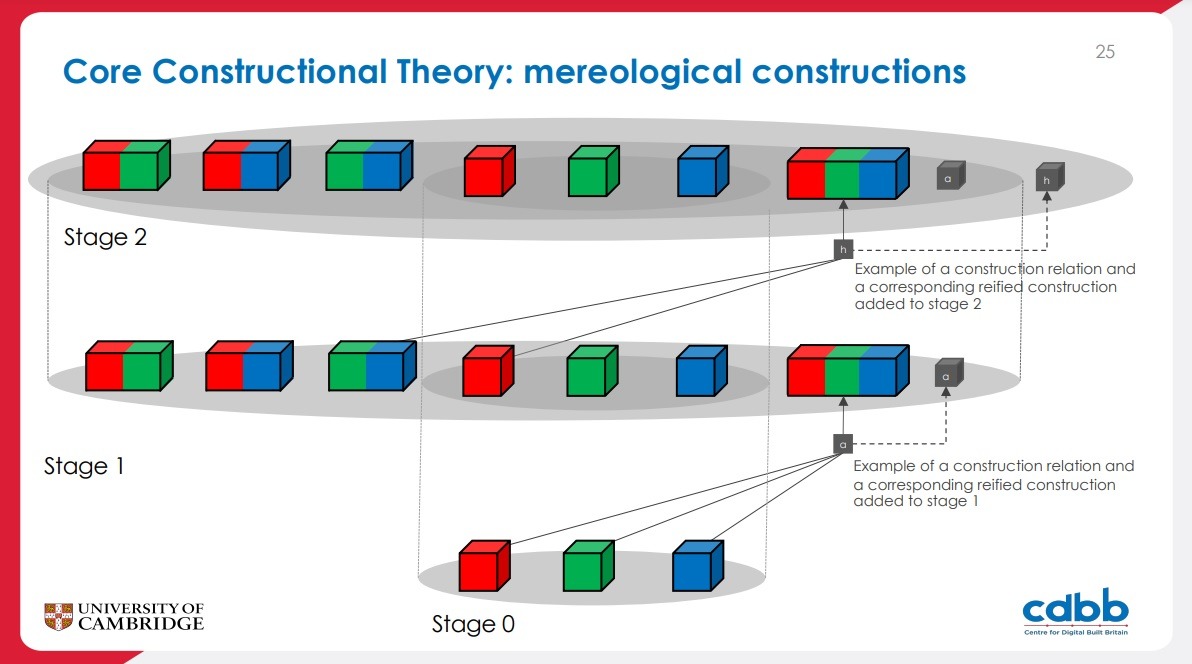
- in keeping with the target TLOs, CCT includes reified constructions, special objects that “log” the structure of the construction process.
Plural quantification
§ gives strength to the theory by allowing to quantify over “collections” of objects in the range of the singular quantifiers.
- Analogy with classes and monadic second-order quantification
§ serves to describe naturally inputs to constructors.
Primitive notions
§ Logic
- Plural logic
§ Constructors
- Set, Sum, Pair
§ Construction process
- Special predicates and constants for types of constructions
§ Stages
- Stage-theoretic notions (is a stage, exists at a stage, follows as a stage)

Axiomatisation




- Plural logic
- Stages
- Initial stages
- What exists at stages
- Constructors
- Reified constructions (“logs” of the construction process)
- Maximal extension of a stage
- Classification
Set theory and mereology in CCT
Using a natural definition of membership, we can deduce the axioms of Zermelo-Fraenkel (ZF) set theory, minus Empty Set, in CCT.
Currently, the axioms of Atomistic General Extensional Mereology (AGEM) are incorporated after defining parthood. At the next stage, we will drop the axioms and deduce them from CCT
Consistency
We provide a mathematical proof of consistency of CCT.
This is done by constructing a model within some chosen metatheory.
CCT is then shown to be consistent relative to this metatheory.
- Morse-Kelley class theory (MK): it adds to ZFC a single layer of classes on top of the sets
- ZFC + an extra axiom stating that there exists an inaccessible cardinal
- ZFC for weakenings of CCT (e.g. plural comprehension restricted to stages or dropping the analogue of Replacement)
CLIF
- To help ensure logical data quality, Paweł Garbacz is working on translating automatically the human-readable axioms of CCT into CLIF.
- This will avoid manual translation errors.
- Owing to the axiom schemas in CCT, the translation is lossy.
- We anticipate further lossy translations to OWL.

Core Constructional Ontology (CCO): a Constructional Theory of Parts, Sets, and Relations
4-Dimensionalism in Large Scale Data Sharing and Integration Newton Gateway to Mathematics
Appendix: informal overview of the axiomatisation
- Plural logic
- Pluralities are non-empty.
- Pluralities with the same members satisfy the same formulas.
- There is a plurality corresponding to every formula satisfied by one thing (“If there is an F , then there are the Fs.”).
2. Stages
- Stages form a convergent, serial partial order.
- Stages are well founded.
- There are infinitely many stages and a limit stage.
- A version of the axiom of Replacement holds for stages
3. Initial stages
- The initial stage is non-empty (there are “givens” at this stage).
- We assume the existence of specific givens serving to represent constructors and other relevant relations (set-elements, whole-parts, tuple-places, supersubsets).
4. What exists at stages
- Everything that isn’t a stage exists at some stage.
- Stages are “cumulative” (everything that exists at earlier stages also exists at later stages).
- Limit stages are “collection” stages.
- Stages with identical domains are identical.
- What exists at a successor stages existed before or resulted from some construction.
5. Constructors
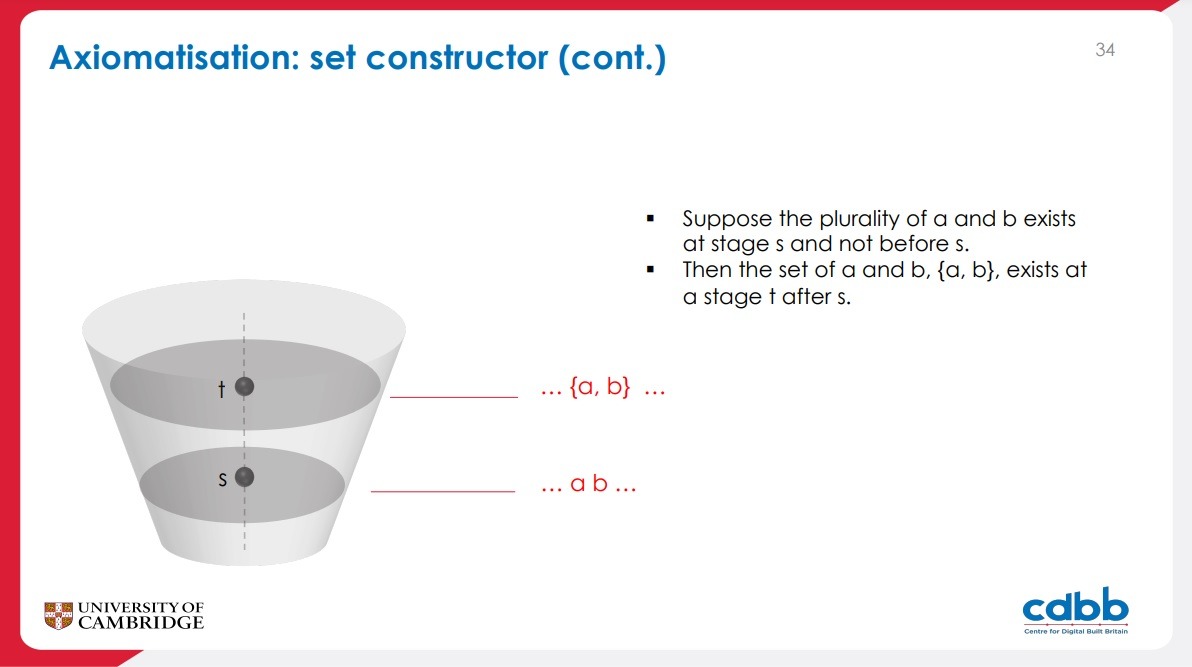
5.1 Set constructor
- Every plurality of objects at a stage is used to construct a set.
- The elements of a set exist before the set.
- Extensionality (two sets are identical iff they have the same elements)
5.2 Sum constructor
- Every plurality of individuals at a stage is used to construct a sum.
- Sums constructed from the same pluralities are the same.
- The sum constructed from the singleton plurality of x is x.
- Two pluralities, one obtained from the other by replacing some objects with their sum, yield the same sum.
- Parthood satisfies the axioms of AGEM.
5.3 Pair constructor
- For any two objects existing at a stage, there is a later stage when they are used to construct a pair.
- The coordinates of a pair exist before the pair.
- Extensionality (two pairs are identical iff their first coordinates are the same and their second coordinates are the same)
6. Reified constructions (“logs” of construction process)
- These axioms ensure that, whenever certain constructions are effected, there are objects that encode this information.
7. Maximal extension of a stage
- These axioms sanction that every stage s has a maximal extension, i.e. a stage obtained by effecting every construction possible at s.
8. Classification
- These axioms partition the domain of the theory in five kinds of entities: individuals, sets, pairs, reified constructions, and stages.