Конкурирующие Пуассоновские процессы

В первой части исследования мы с вами выяснили, что голы, забитые командой в хоккейном матче – это Пуассон, пропущенные командой голы – тоже Пуассон. Теперь перед нами стоит задача: выяснить, что происходит, когда два Пуассоновских процесса (забитые и пропущенные командой голы) конкурируют между собой. Какова вероятность того, что команда в матче забьет больше голов, чем пропустит; забьет столько же, сколько пропустит и, наконец, забьет меньше голов, чем пропустит?

И для начала нам нужно выяснить, являются ли показатели забитых и пропущенных голов независимыми; если они окажутся независимыми друг от друга, расчеты станут значительно проще. Итак, зависят ли забитые хоккейной командой голы от пропущенных ею голов? Ответ неоднозначный: и да, и нет.

• Для того, чтобы получить ответ на этот вопрос, нам необходимо проверить, существует ли для отдельных команд корреляция между забитыми и пропущенными в матчах шайбами. Когда число забитых командой в матче голов растет, снижается ли число пропущенных ею голов? Если команда забивает во время матча мало голов, будет ли она пропускать в нем много голов? Бывают ли команды, которые, когда забивают в матче много голов, при этом еще и много пропускают; а в тех матчах, в которых забивают мало, так же мало и пропускают? Чтобы это выяснить, мы должны для каждой отдельно взятой команды сравнить показатели забитых и пропущенных в каждом матче голов, проверив таким образом, есть ли между ними какая-то взаимосвязь.
• Проверив эти данные, мы придем к выводу: показатели забитых и пропущенных голов статистически независимы (то есть, достаточно независимы). В 2004 году только одна команда показала статистически значимую корреляцию (это был Вашингтон с коэффициентом -0,29). В 2003 году статистически значимых корреляций не было. Данные за другие годы не проверялись, поскольку это требует анализа голов в каждой игре, но я полагаю, что статистически значимая корреляция встречается редко. Это скорее исключение, чем правило. Итак, с этой точки зрения мы можем сделать вывод, что показатели забитых и пропущенных голов независимы друг от друга.
• Более тонкий вопрос заключается в следующем: взаимосвязаны ли показатели забитых и пропущенных голов с изменением разницы в счете по ходу матча? Здесь ответ безоговорочно положительный, и тому есть есть наглядное подтверждение. Причина кроется всё в тех же старых проблемах – овертаймах и эффекте завершения игры (об этом мы говорили в первой части исследования). 
• Однако к этим причинам можно добавить еще кое-что: дело в том, что команды могут менять (и меняют) защиту на нападение. Проигрывая, команда обычно пытается играть более открыто, чтобы повысить шансы на ничью. И напротив, поведя в счете, команда пытается больше обороняться, чтобы увеличить шансы на сохранение лидерства. Чем меньше разница в силе команд, тем более выраженными становятся эти два эффекта. Возможно, эти два эффекта компенсируют друг друга на дистанции (о чем свидетельствует наш тест на независимость), но не факт. По большей степени с этими проблемами можно справиться, так что сейчас мы продолжим наше исследование, предполагая независимость забитых и пропущенных голов, и вернемся к этому вопросу позже.

Вероятность ничьей

Итак, мы предполагаем, что забитые и пропущенные голы являются независимыми Пуассоновскими переменными со средними μ и λ соответственно. Исходя из этого, вероятность того, что забитые (GF) и пропущенные (GA) голы принимают одно и то же значение – это вероятность наступления ничьей со счетом 0-0, плюс вероятность ничьей со счетом 1-1, плюс вероятность ничьей со счетом 2-2 и так далее. 

Математически это выглядит так:

Проблема с выражением для вероятности ничьей состоит в том, что оно включает в себя суммирование, которое теоретически является бесконечным, хотя на практике и возможно сократить вычисление при достаточно большом k. В Excel это означает суммирование k столбцов (или строк) вычислений или же написание функции, которая выполняет цикл k раз.

Замкнутая формула (то есть, без циклирования) для этой вероятности была бы более предпочтительной, поскольку она существенно повышает эффективность вычислений. И такая формула действительно есть: 

Она является модифицированной функцией Бесселя первого рода (нулевого порядка), которая включает в себя сумму

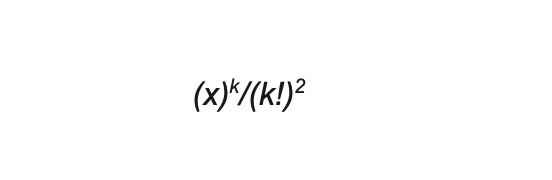
где k равен от 0 до бесконечности. Это означает, что для команды, у которой в среднем μ забитых и ν пропущенных голов за игру, вероятность ничьей (без сокращения или циклирования формулы) можно выразить как:

Если бы функция Бесселя была сложной в использовании, все это не было бы нам особо полезным. Но, к счастью, ее достаточно просто использовать в Экселе:

где μ = забитые за игру голы; ν = пропущенные за игру голы.

Ниже приведен график вероятности ничьей. Хочу обратить ваше внимание: мы рассматриваем не один матч, а усредненные результаты. То есть, если бы один и тот же матч проводился бесконечное множество раз, и команда в среднем за игру забивала бы определенное количество голов и пропускала бы определенное количество голов, мы бы с помощью данного графика увидели, с какой вероятностью наступит ничья. Этот график демонстрирует, что:

• вероятность ничьей уменьшается с ростом результативности;
• вероятность ничьей уменьшается с увеличением разницы между забитыми и пропущенными голами.

И, наконец, давайте посмотрим на важное пограничное условие. Если у команды в среднем 0 забитых и 0 пропущенных голов, у нас всегда будет ничья (то есть, ничья наступит с вероятностью в 100%). Это простое выражение для вероятности ничьей удовлетворяет следующему условию: EXP (0) = 1 и BESSELI (0,0) = 1. Кроме того, функция вероятности изящно стремится к нулю. 

Вероятность победы, рассчитанная на основе Z голов

Формула для вероятности ничьей прекрасно переносится на вероятность победы на основе z голов (при условии, что z больше или равно 0):

где μ = забитые за игру голы; ν = пропущенные за игру голы.

В Экселе вероятность победы на основе z голов выглядит следующим образом:

Обратите внимание, что при дальнейшем обобщении (ABS (z)) это выражение является справедливым для всех z, включая проигрышные ситуации (выигрыш по –z голам). Я буду использовать сокращение PrWinBy (z, μ, ν), чтобы обратиться к этому расчету для оценки вероятности выигрыша по z голам. Также мы обратимся к нему в качестве формулы Скеллама. 

Формула Скеллама говорит нам, что вероятность выигрыша с использованием z голов является функцией z, общего контекста подсчета очков (μ+ν) и разницы между тенденцией к набору забитых и пропущенных голов. Чтобы убедиться в этом, давайте посмотрим на три части формулы:

• EXP (- (μ+ν)) чувствительна только к общей результативности. Если μ+ν постоянны, то она безразлична к соотношению μ и ν. По мере увеличения μ+ν результат уменьшается. Он нечувствителен к разнице голов z. Эта часть формулы аналогична части EXP (-μ) из формулы Пуассона. Она равна вероятности нуля голов и эффективно масштабирует остальную часть выражения.
• (μ/ν) ^ (z/2) чувствительна как к z, так и к разнице (соотношению) между μ и ν. Когда z=0 (то есть, при ничьей), это выражение принимает значение 1. Когда μ=ν, это выражение принимает значение 1. Когда z> 0 и μ>ν, это имеет положительное влияние на вероятность. Для константы μ/ν (> 1) вероятность возрастает с увеличением z.
• BESSELI (2*SQRT(μ*ν), ABS (z)) чувствительно к z, к разнице (соотношению) между μ и ν и к общей результативности. BesselI – это понижающая функция ABS (z), а также возрастающая функция μ*ν (которая увеличивается по мере увеличения общего количества очков). Где в формуле отражается соотношение между μ и ν? 2*SQRT(μ*ν) – еще одна мера общей результативности (когда μ=ν, она равна μ+ν). Но это выражение также обладает следующим свойством для μ+ν = constant: чем больше разница между μ и ν, тем меньше будет выражение (то есть, √‎5x5>√‎4x6>√‎3x7>√‎2x8>...). Следовательно, аргумент функции Бесселя больше, когда μ и ν близки по значению, и меньше, когда они расходятся.

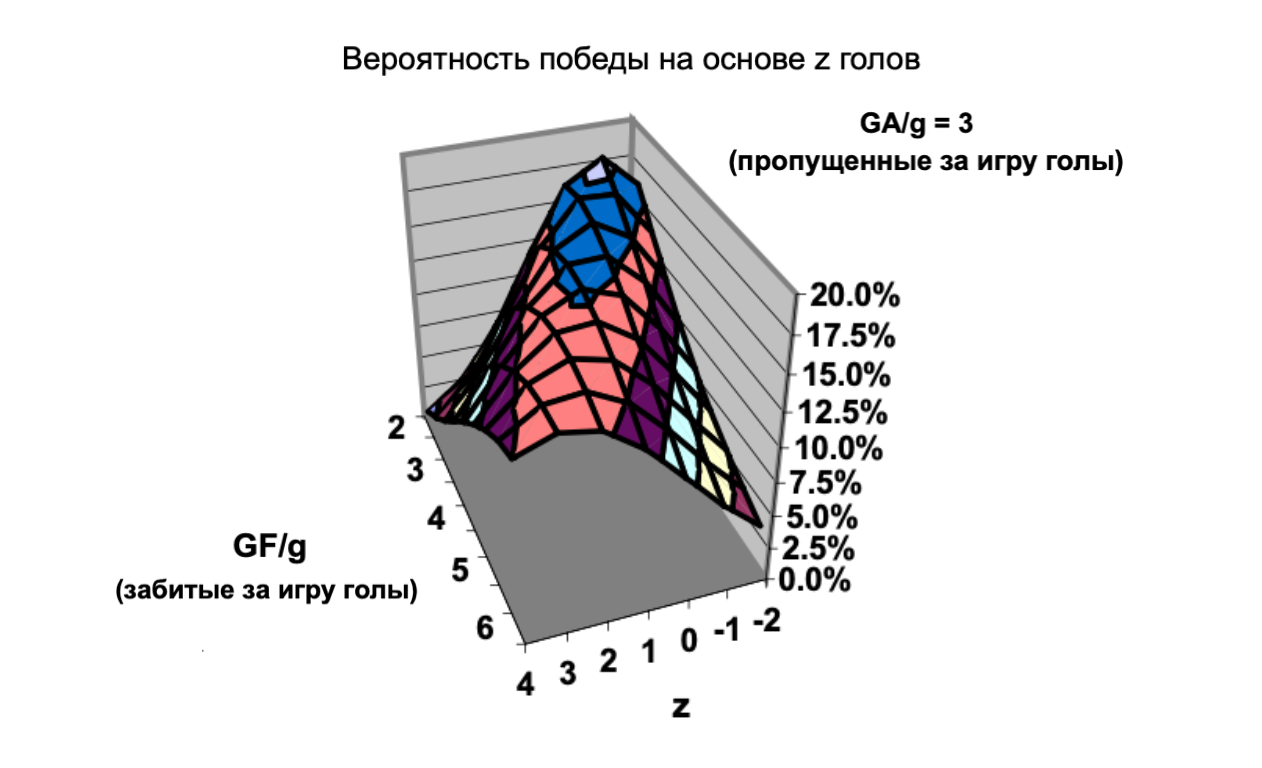
График вероятности выигрыша по z голам, позволяющий варьировать забитые (GFg) и пропущенные (GAg) голы, очень похож на график ничьей, который мы рассматривали выше. Чем больше разница забитых и пропущенных голов, тем ниже вероятности низкорезультативных игр, как мы уже увидели на пресловутом графике ничьей. На графике с ростом z поверхность вероятности становится более плоской (вероятность уменьшается под влиянием забитых и пропущенных голов), а точка максимальной вероятности отклоняется.

Ниже приведен график вероятности выигрыша по z голам, позволяющий варьировать z и забитые голы, но при этом пропущенные голы (GAg) неизменно остаются равными 3. Точка максимальной вероятности для всех значений z наступает, когда разница забитых и пропущенных голов становится равной z. То есть, у команды, которая в среднем на дистанции забивает 5 голов, а пропускает 3, вероятность выиграть с преимуществом в 1 гол выше, чем вероятность ничьей, а вероятность выиграть в 3 гола выше, чем в 4. Но самая большая вероятность у данной команды – выиграть с преимуществом в 2 гола.

Поскольку игра должна закончиться победой, ничьей или поражением, это описывает распределение вероятностей для разницы голов при условии, что μ = забитые за игру голы; ν = пропущенные за игру голы. На графике ниже показана теоретическая вероятность выигрыша на основе разницы голов, базирующаяся на данных сезона 1999-2000 года. На нем фиолетовым цветом обозначена кривая которая описывает распределение вероятностей для разницы голов при условии, что μ = забитые за игру голы; ν = пропущенные за игру голы, и имеет стандартное отклонение, пропорциональное среднему геометрическому забитых и пропущенных голов (то есть, √GFg x GAg).

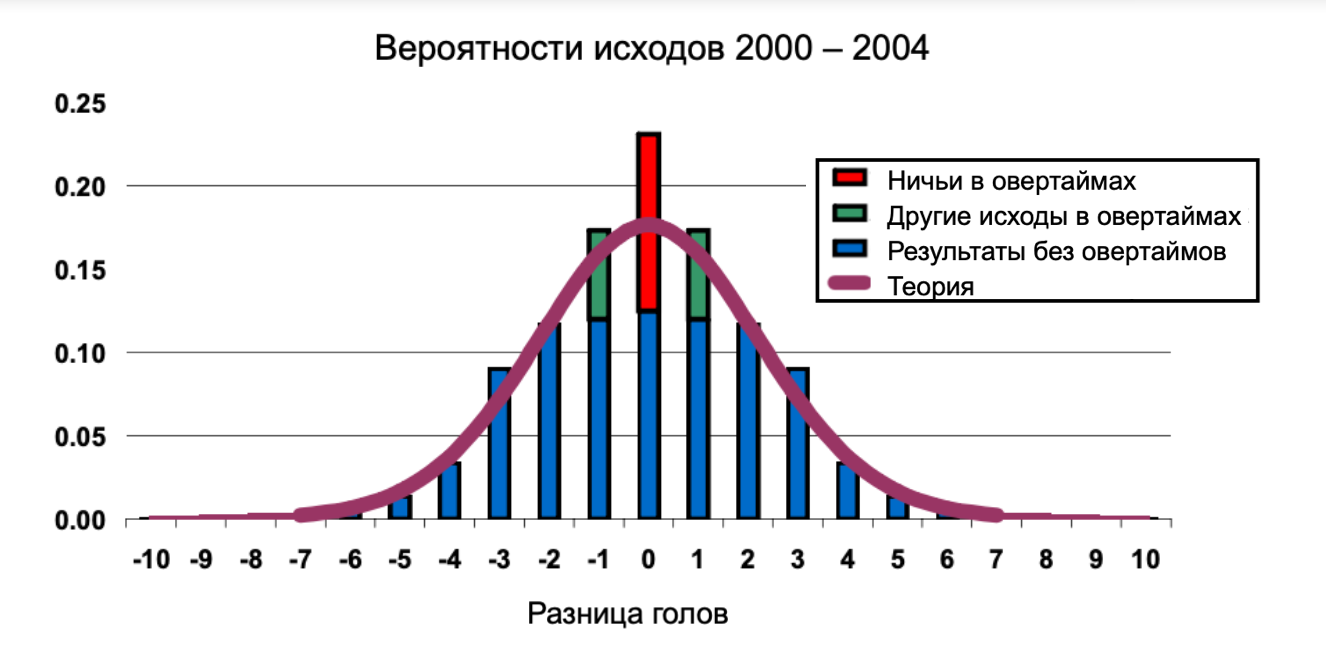
Также на этом графике в виде столбцов представлено фактическое распределение разницы голов, наблюдаемое с сезона 1999-2000гг. по 2003-2004 гг. Данные столбцы являются симметричными. К примеру, столбец со значением +3 равен столбцу -3, так как забитые одной командой голы – это голы, пропущенные другой командой. Если матч закончился со счетом 4-1, мы добавим этот матч в столбец +3 и в столбец -3.

Убрав отрезки столбцов, помеченные зеленым, и представив красный отрезок синим, вы увидите результаты матчей за основное время (то есть, без учета овертаймов). Но если вы, напротив, оставите зеленые отрезки и уберете отрезок, помеченный красным, то увидите результаты матчей с учетом овертаймов. Объясню подробнее, почему так происходит. Столбец 0 – это ничьи. Для основного времени столбец 0 – это синий плюс красный отрезки. Но поскольку в овертайме часть матчей так и заканчивается без забитых шайб (синий отрезок), а в части матчей забиваются шайбы (красный отрезок), то красный отрезок делится пополам на два зеленых.

Из этого графика мы можем заметить, что наша теория упускает нечто важное. Внимательно сопоставим фиолетовую кривую со столбцами без учета овертаймов (синие+красный). Мы увидим, что теория предсказывает меньше ничьих и меньше матчей с разницей в 3 гола, а также больше матчей с разницей в 1 гол по сравнению с тем, что мы получаем в действительности. 

Если же мы сопоставим фиолетовую кривую со столбцами с учетом овертаймов (синие+зеленые), то увидим, что теория предсказывает меньше игр с разницей в 1 гол и больше ничьих. 

Это является главным свидетельством того, что забитые и пропущенные голы зависят от разницы забитых и пропущенных голов, и мы уже знаем основные причины. Влияние овертаймов очевидно: без учета овертаймов у нас «слишком много» ничьих, а с учетом овертаймов – «слишком мало» ничьих. Другие причины: факт, что команды в зависимости от счета могут менять защиту на нападение и обратно, а также эффект завершения игры, имеют более тонкое влияние. Позже мы расширим данную теорию, чтобы попытаться справиться с влиянием этих причин.

Эти теоретические вероятности разницы голов близки к нормальному распределению. Среднее значение нормального приближения пропорционально разнице забитых и пропущенных за игру голов (GFg – GAg), а стандартное отклонение пропорционально √GFg x GAg. Но конкурирующие вероятности Пуассона значительно отличаются в центре распределения. Нормальное приближение будет менее достоверным, поскольку забитые и пропущенные голы расходятся, и симметрия нарушается. В частности, рассматривая случай, когда забитые голы равны нулю, тогда распределение вероятностей сводится к Пуассону.

Вероятность победы

Давайте начнем с рассмотрения вероятности победы в матче с учетом того, что игра определяется z голами (то есть, проигрыш в z голов или выигрыш в z голов). Вероятность выигрыша в таком матче составляет:

Сокращаем все, что можно сократить в числителе и знаменателе, и нам остается следующее выражение:

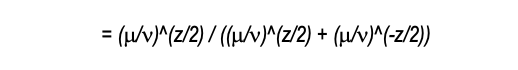
А теперь умножим числитель и знаменатель на (μ/ν) ^ (z / 2) и получим:

Это выражение должно показаться ужасно знакомым каждому, кто хотя бы немного возился с формулами вероятности победы: это формула Пифагора, обобщенная экспонентой, равной показателю z. Когда z = 2, мы получаем традиционную формулу Пифагора.

Существует следующий способ, который позволяет нам взглянуть на вероятность победы: это вероятность победы с разницей в 1 гол, умноженная на вероятность победы в 1 гол + вероятность победы в 2 гола, умноженная на вероятность победы в 2 гола и так далее.

Математически это выражается так:

Где pk – это вероятность завершения матча с разницей в k голов. Для любых заданных μ и ν мы всегда можем найти такой показатель z:

К сожалению, z не всегда и не обязательно является постоянным для всех μ и ν, и это весьма интересное наблюдение. Оно дает обоснование пифагорейской взаимосвязи (средневзвешенное значение вероятностей выигрыша по всем разницам забитых голов) и объясняет, почему 2 не может быть лучшей экспонентой (почему это должно быть лучшим z?). Но для вычислений это не несет какой-то особой пользы.

Вероятность выигрыша лучше выразить с помощью приведенной ниже таблицы вероятностей исходов. (μ = ν = 2,57). 

Зеленые ячейки представляют случаи, когда забитых голов больше, чем пропущенных. Вероятности в ячейках – это вероятности комбинаций забитых и пропущенных голов (например, вероятность победы со счетом 4-2 составляет 0,035). Чтобы получить вероятность выигрыша, мы должны сложить значения в зеленых ячейках.

Это можно сделать тремя способами. Вероятность победы – это:

1. Вероятность победы в 1 гол + вероятность победы в 2 гола +... и так далее (здесь мы складываем значения по диагонали).

2. Вероятность забить 1 гол и пропустить менее 1 гола + вероятность забить 2 гола и пропустить менее 2 голов +... и так далее (складываем столбцы).

3. Вероятность пропустить 0 голов и забить более 0 голов + вероятность пропустить 1 гол и забить более 1 гола +... и так далее (складываем строки).

Математически эти три метода могут быть выражены таким образом:

где μ и ν – это, соответственно, тенденция к забиванию и пропусканию голов за игру (то есть, GFg и GAg).

К сожалению, любое из этих выражений не имеет решения с помощью замкнутой формулы. Первый метод состоит только из одного цикла и теоретически может обеспечить более высокую точность, поскольку функция Бесселя здесь не сокращается. Кроме того, такой подход позволяет напрямую изменять вероятности для овертаймов и эффекта завершения игры (как в примере ниже). Остальные два метода включают двойное суммирование, хотя оба могут быть запрограммированы как один цикл. Чтобы не прибегать к зацикливанию, нам необходимо использовать значительное (10 или более) количество столбцов или строк в таблице.

Все три формулы суммирования вероятностей выигрыша дадут одинаковый результат. Мы будем использовать сокращение PrWin (μ,ν) для описания любого из этих вычислений. Результатом такого конкурирующего Пуассона является точная вероятность выигрыша (с учетом некоторых оговорок). Это необходимо противопоставить Пифагору и его производным, которые являются эмпирическими и лишь приблизительными.

Давайте проверим формулу Скеллама, беря во внимание другое крайнее условие. Если команда забивает в среднем за игру 0 голов, а пропускает 1, она не может выиграть. Формула Скеллама подтверждает это, возвращая 0 для всех положительных вероятностей победы. Также формула Скеллама говорит о том, что 36,8% (EXP (-1)) матчей закончатся ничьей. 

Следовательно, мы можем сделать вывод, что с вероятностью 0,632 команда проиграет. 

Если команда забивает в среднем 1 гол, а пропускает 0 голов, она не может проиграть. Само собой разумеется, что с вероятностью 0,632 команда должна одержать победу. Что формула Скеллама говорит нам о вероятности победы? К сожалению, выражение для вероятности выигрыша по z голам не применимо к ситуациям, когда количество пропущенных голов равно 0, поскольку тогда в нашей формуле появляется деление на 0. Но если вы изучите предел вероятности выигрыша (то есть, суммирование по всем выигрышным полям), удерживая GFg константа 1, и если GAg стремится к нулю, вы получите 0,632. Этот результат, как и ожидалось, предполагает, что при данном условии наша теория все еще верна. Практическое следствие состоит в том, что забитые (GFg) и пропущенные (GAg) голы следует заменять чем-то вроде MAX (GFg, 0,0001) и MAX (GAg, 0,0001) соответственно каждый раз, когда программируется формула Скеллама.

Итак, мы с вами разобрали, что происходит, когда два Пуассоновских процесса, забитые и пропущенные командой голы, конкурируют между собой, и выяснили, как на основе данной формулы рассчитать вероятность победы в матче. Эта информация пригодится нам в следующей части исследования.