Коли ти повернешся додому? Або чим скінчаються походеньки п'янички

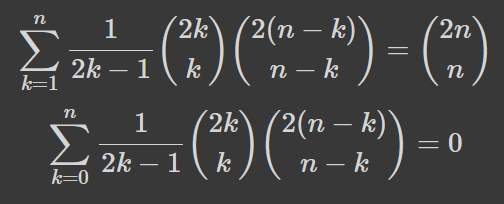
Розглянемо звичайні випадкові блукання, де п'яничка щосекунди робить крок вліво або вправо однакової довжини. Для реалістичності можете розглянути проходження ним алкотесту, себто рух вперед і відхилення від середньої лінії, яке щокроку збільшується або зменшується на певну одиницю. Постає (в кого?) питання: скільки у нього є шляхів закінчити там, де він почав? Або ж, скількома способами він може повернутись на лінію?

З куди менш наближених до реальності прикладів: скількома можливими шляхами ціна акцій повернеться до початкового рівня? Ця кількість є певно головною величиною для розрахунку ймовірності цього самого повернення. Більше застосувань ви можете віднайти у власних областях.

Кількість шляхів навпростець

Очевидно, що аби закінчити на лінії, кількість зроблених кроків має бути парна, 2n. Ще очевидніше те, що кількість лівих та правих кроків у такому разі однакова і рівна n. Тоді кількість шляхів (траєкторій) рівна кількості способів упорядкувати n лівих та n правих кроків у рядок довжиною 2n. Якби ліві кроки відрізнялись між собою, як і праві, то ця кількість була б рівна (2n)!, а так як вони однакові, то кожну унікальну перестановку лівих кроків ми враховуємо таким чином n! разів, як і правих. Остаточно, кількість шляхів рівна:

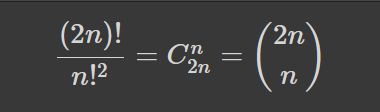
Наприклад, легко переконатись, що є 6 послідовностей з 4 кроків, які закінчуються де почались, і вони зображені на малюнку:

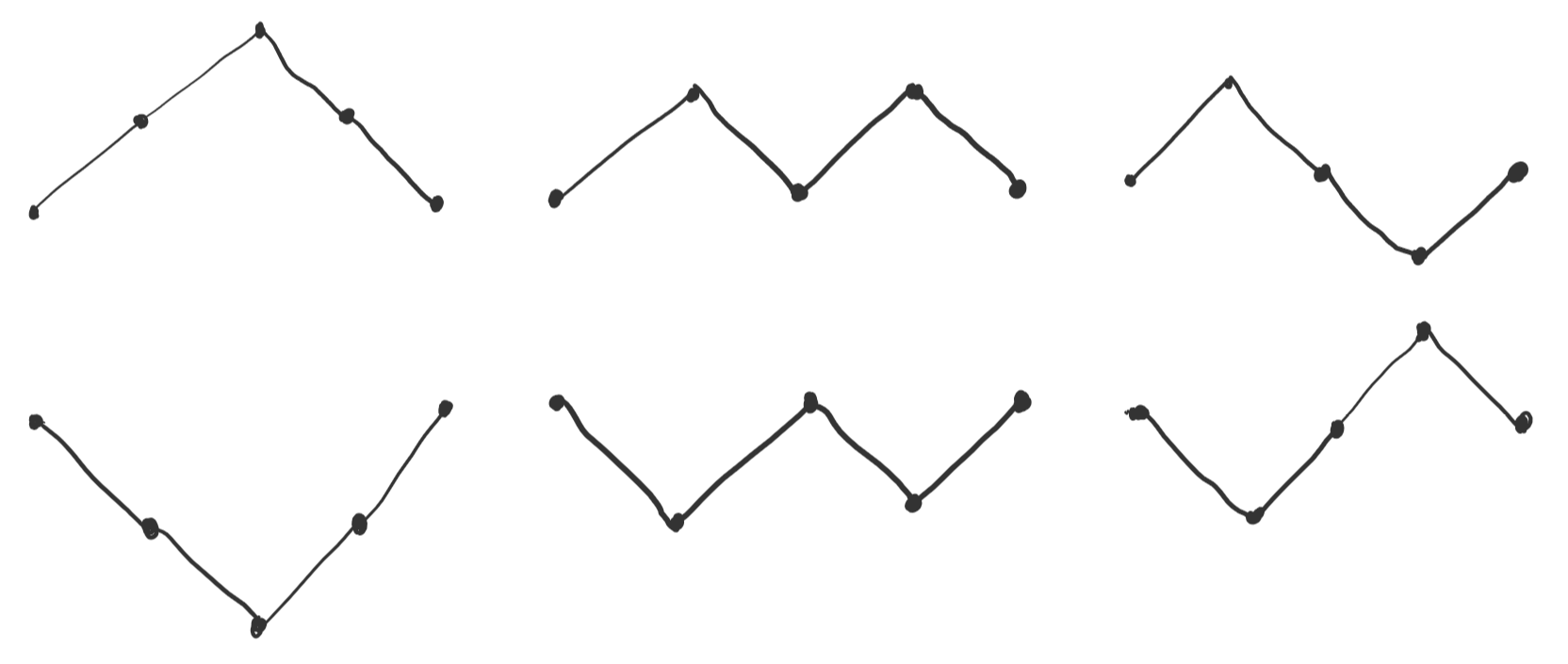
Тепер формула має бути зрозуміліша. Особливо, якщо зробити наступне геометричне перетворення:

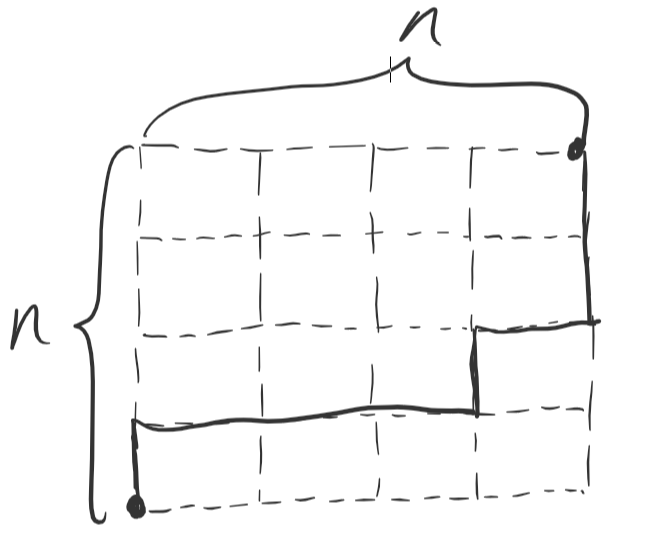
Тобто кількість способів серед 2n відрізків обрати n з них лівими (решта автоматично стають правими). Так як порядок вибору не грає ролі (обрати перший та третій відрізок лівими це всерівно що обрати лівими третій та перший), то це кількість комбінацій з 2n по n, яка й дається вищенаведеною формулою.

Кількість Одіссей

Цікавішим, і часто застосовнішим, буде питання про те, скільки є способів повернутись на лінію, не перетинаючи чи торкаючись її? Це еквівалентно кількості способів, при яких повернення через 2n кроків буде першим за весь час. У випадку n=2, 2n=4 лише ліві два шляхи на малюнку вище задовольняють цю умову. У середніх двох шлях торкається лінії, а у останніх двох -- перетинає її; називатимемо такі шляхи тими, що досягають лінії. Як обрахувати цю кількість? Зауважимо, що відтепер ми виключаємо випадок n=0 з розгляду (очманіти, багато ж втратили).

Певно найзастосовніший прийом у теорії ймовірностей та комбінаториці полягає у обрахунку доповняльної величини. Як от, ймовірність, що щось трапиться щонайменше один раз, зазвичай обрахувати значно складніше і громіздкіше, ніж обрахувати ймовірність того, що це щось ніколи не трапиться, і відняти її від одиниці. Тож тут ми помітимо і використаємо наступне:

1) Кількість шляхів, які не досягають лінії, рівна кількості всіх шляхів мінус кількість шляхів, які щонайменше раз її досягають.

2) Шляхи, які досягають лінії, можна в точці першого досягнення розбити на два окремі шляхи: до, який не досягає лінії, та після, який досягає її або ніт. Таким чином, множина шляхів, які вперше досягають лінії на другому кроці, не перетинається з множиною шляхів, які вперше досягають лінії на четвертому кроці, і так далі.

Величини в обох пунктах ми вміємо рахувати. Шукана кількість рівна 2C_{n-1}, де C_{n-1} -- (n-1)-ше число Каталана (просто назва). Кількість в пункті 1 наведена у формулі вищі, а в пункті 2 це сума кількостей для кожної точки (кроку 2k) на лінії, де її вперше досягає певний шлях. Кількість цих певних шляхів тоді рівна добутку кількості бездосяжних шляхів до (2С_{k-1}) та просто шляхів (які починаються і закінчуються на лінії) після (C_{2(n-k)}^(n-k)). Тоді маємо рівняння:

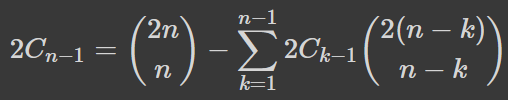
Сума, яка міститься у рівнянні, зветься згорткою, бо є сумою добутків вигляду a_k b_{n-k}. Обрахуємо перші кілька чисел:

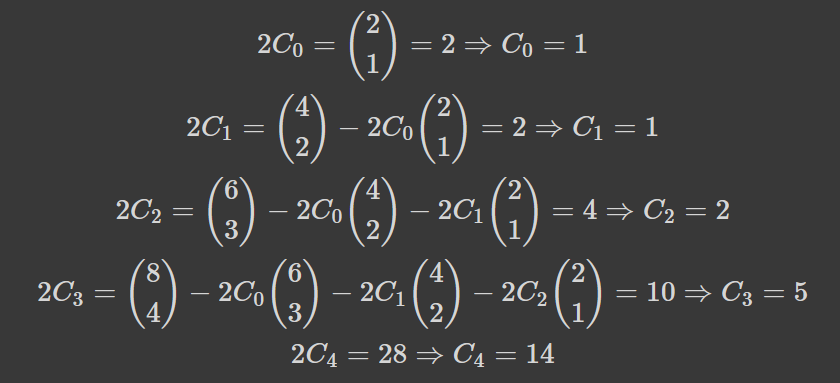
Це наштовхує на гіпотезу, яка не те щоб полегшувала нам життя:

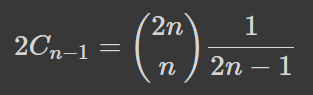
Себто кількість шляхів, які не досягають лінії, в (2n-1) разів менша за загальну кількість шляхів -- напрочуд цікавий факт, інтуїтивне пояснення до якого я сподіваюсь якось віднайду. Вцілому ж можна помітити, що кількість таких шляхів рівна кількості шляхів між точками 1-1 або 2-2 на малюнку нижче, які не неретинають, проте можуть торкатись діагоналі між цими точками.

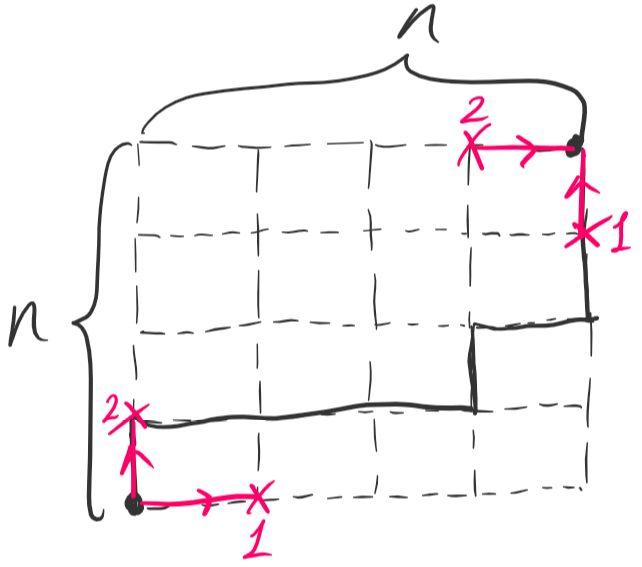
Обрахунок кількості цих шляхів описаний у Вікіпедії на сторінці про числа Каталана, який я безсоромно скопіюю сюди:

Формулювання формули

Підставимо цю формулу у наше рівняння і спробуємо її довести:

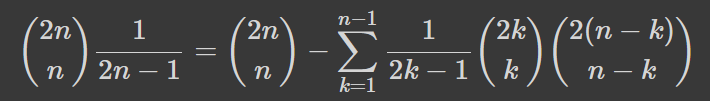
Її можна переписати трьома наступними способами:

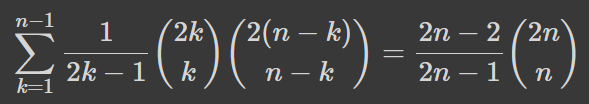
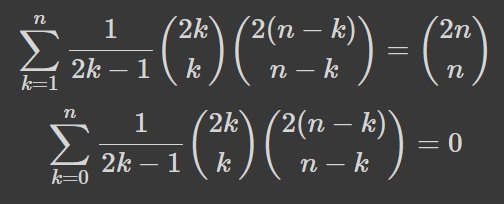
Така красива і без доведення. Ба більше, якщо взяти оригінальну формулу, замінити k на n-k, та додати до самої себе, то вийде:

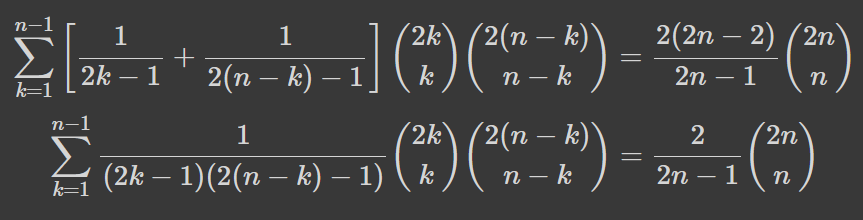
Але обережно, тут ми поділили на (2n-2), яке рівне нулю при n=1. Тобто цей вигляд формули не є застосовним для випадку n=1, а тому в подальшому доведенні його виключаємо. Тепер, після вираження біномів з дробами через числа Каталана отримаємо наступне співвідношення:

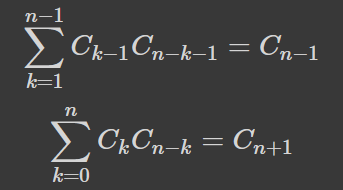
Де в другому ми збільшили n на 2 та зменшили k на 1. Це хоч і збігається з формулою з Вікіпедії, проте досі не є доведеним твердженням. Тож як довести саму формулу і отримати обід в Пузатці?

Твірна, ряд Маклорена, та добуток безкінечностей

Часто (наскільки?) комбінаторній функції a_n можна співставити ряд:

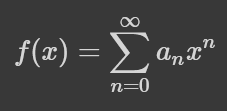
Який для певних x навіть збігатиметься до значення функції f(x). Отримана функція зветься твірною для даної послідовності. Для біноміального коефіцієнта ця функція є:

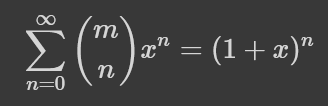
біномом Ньютона. Було враховано, що біноміальні коефіцієнти для n>m рівні нулю, тому насправді ряд має всього лише m+1 доданків, а не безкінечну кількість. З ще знайомих прикладів, як от кількість способів обрати нуль елементів з n:

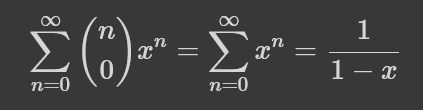
Цей ряд збігається для всіх -1<x<1. Ще гарним прикладом є кількість n-цифрових чисел у системі числення з основою b:

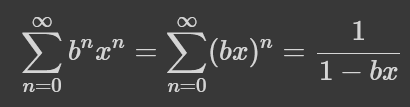
Цей ряд збігається для ще меншого проміжку x: -1/b<x<1/b. Остаточно, з менш надихаючих прикладів, кількість перестановок з n елементів:

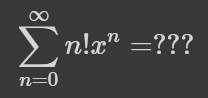
Яка дає ряд, що збігається хіба що для x=0. З цієї ненадихаючої ноти можна перейти в обнадіюючу: продиференціюємо нашу геометричну прогресію:

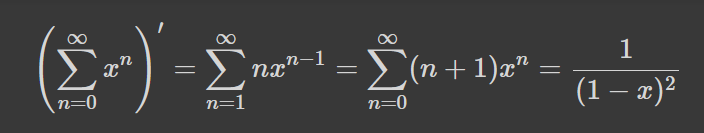
Абсолютно не вражаюча кількість способів прокласти шлях з n лівих та одного правого повороту. Диференціювання ж k разів дасть ряд для кількості способів розставити k різних ресторанів та n однакових вікон з працівницями на вулиці багряних смолоскипів:

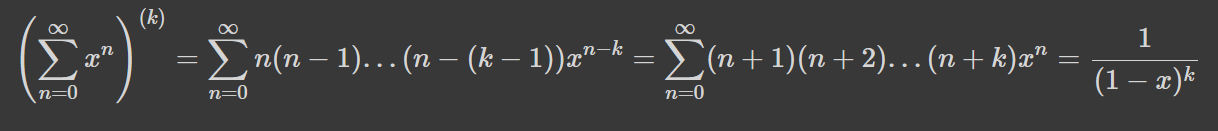
Остаточно, пригадаємо, що всі форми формули, яку ми хочемо довести, мають вигляд згортки, а саме:

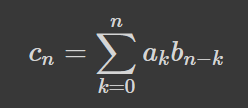
Твірна дарує нам спосіб боротьби з цим. Домножимо обидві частини рівняння на x^n та просумуємо ряди:

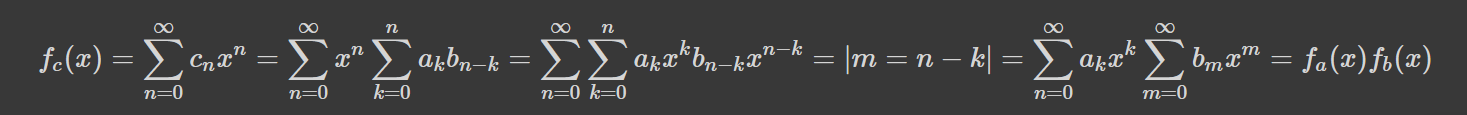
Як бачимо, якщо одна послідовність є згорткою двох інших, то її твірна рівна добутку твірних цих послідовностей. Надзвичайно корисний факт, який ми зараз і продемонструємо.

До справи

Підемо зворотнім шляхом і подивимось, яку послідовність породжує наступна твірна:

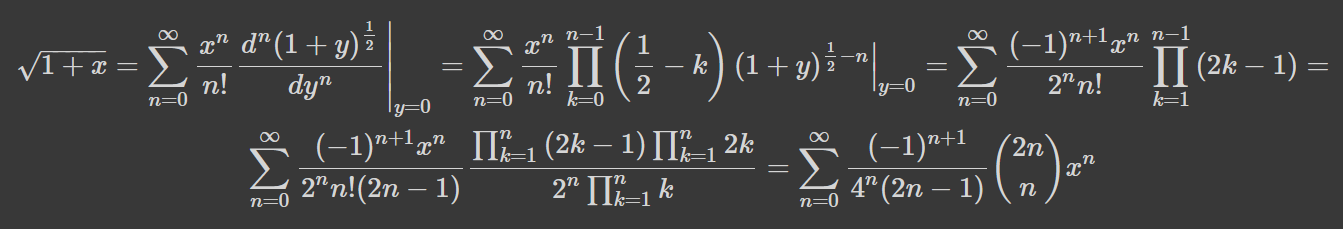
Щось знайоме, чи не так? Легкою заміною отримуємо навіть краще:

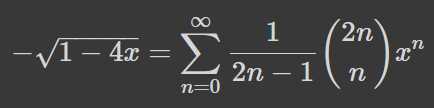
Як бачимо, прийшли до нашої гіпотези! А що станеться, якщо помножити цей ряд сам на себе?

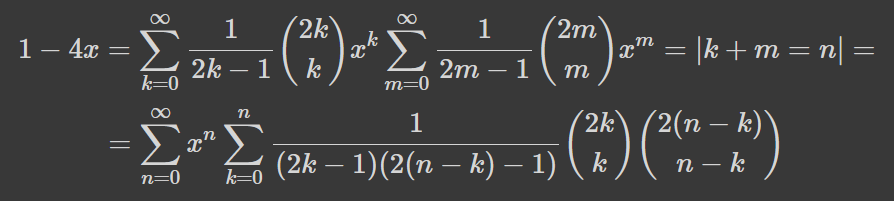
Де ми знову використали заміну змінних у підсумовуванні, аби звести все до вигляду a_nx^{k+m=n}. Це вам має нагадати одну з формул згори, а саме:

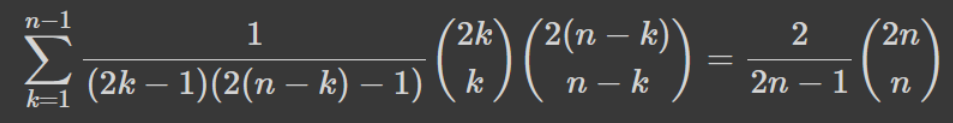
Очманіти! Чи не так? Прилаштуємо доданки k=0 та k=n куди потрібно. Маємо:

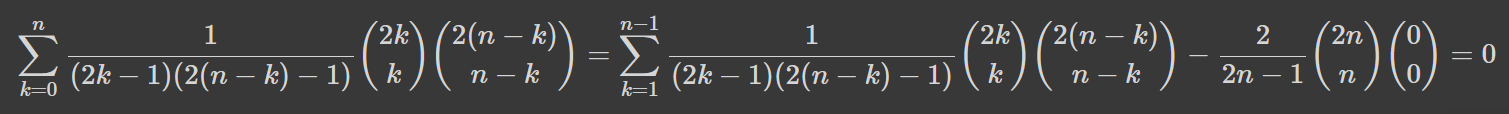
Де кількість комбінацій обрати 0 елементів з 0 рівна 0!/0!^2=1. Звідки ми взяли найправіший нуль? Все просто: ми доводимо рівність для n>1, а в отриманому нами ряді всі члени, починаючи з x^2, мають нульовий коефіцієнт. Тож, ми довели формулу! А разом з тим і рекурентне співвідношення на числа Каталана, з якої воно слідує! Перемога!

Підсумовування та альтернативні підходи

Ми довели формулу наступним чином:

1) Звели її до вигляду згортки послідовності самої з собою.

2) Знайшли (як?) твірну функцію, яка б давала цю послідовність.

3) Помножили твірну фунцію саму на себе і прирівняли відповідні члени отриманого ряду.

Цей метод значно універсальніший, ніж може здатись. Ба більше, перший крок є необов'язковим: замість нього можна було б знайти твірну другого множника, а саме загальної кількості шляхів. Продиференціюємо нашу твірну:

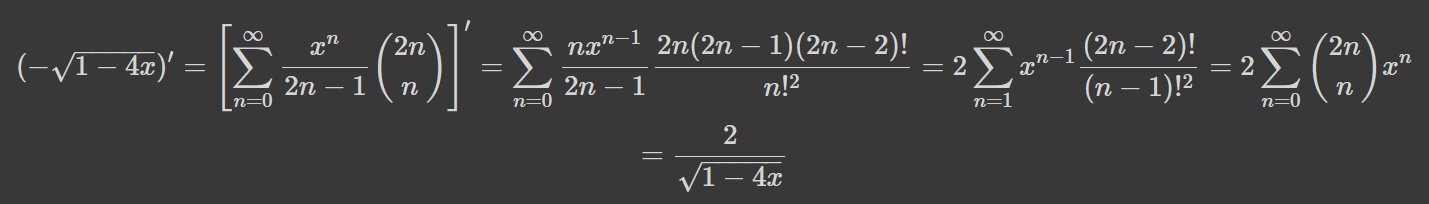
Як бачимо, це твірна найпершої знайденої послідовності в цій статті. Скорочення на двійку і перемножування двох твірних дасть:

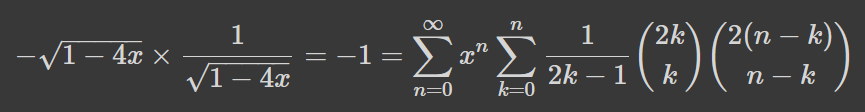
Що для натуральних n (нагадуємо, випадок n=0 до розгляду не беремо) дає одне з формулювань оригінальної формули. Доведення вдруге закінчено!

Очевидно, найскладнішим кроком є знаходження підходящої твірної, і завдання це в загальному випадку анітрохи не просте. Проте для більшості базових випадків її може бути легко вгадати. Головне не боятись експериментувати з формою вже відомих твірних функцій, що ми робили тут, як от прибирання степенів двійки чи переписування подвійних факторіалів.