Как устроены GPT чат-боты. Часть 1

Мне внезапно стало интересно, как устроены внутри все эти ChatGPT штуки, которые прям волшебно как-то работают. Поэтому я немного нырнул в тему (и сразу вынырнул, там бескрайняя бездна какая-то, может засосать) и здесь хочу буквально крупными ламерскими мазками расписать, что я там увидел. Ботал я в основном по видосам Andrej Karpathy (далее Андрей), их и буду вставлять в текст.

В первую очередь текст пишу для тех, кто захочет пройти по моему пути. Я крайне рекомендую сделать это, если хочется действительно что-то понять. Ну а я здесь суммирую штуки, над которыми больше всего пришлось думать, гуглить отдельно и которые хотелось бы сначала увидеть в более крупном масштабе, если бы я изучал это заново.

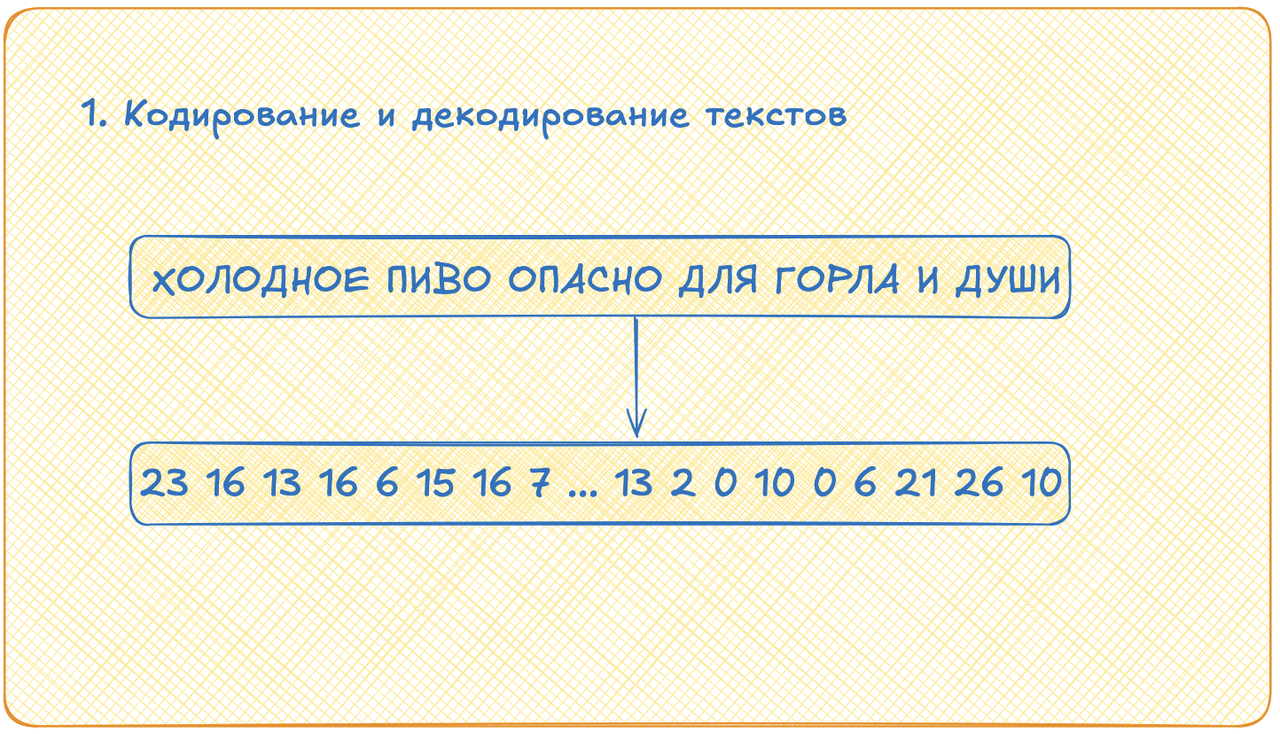
Кодирование и декодирование текста

Первое, что надо разобрать это кодирование и декодирование текста. Здесь всё просто, но меня напугал размер и масштаб! Мы берём все наши тексты, разрезаем их на токены (например, на буквы), все эти токены складываем в отсортированный список. Теперь каждый токен кодируется индексом в этом списке. Всё. Декодируется текст из индексов аналогично: берём число, смотрим, что лежит в списке по индексу, равному этому числу, получаем токен.

Теперь чуть глубже. Каждое такое число будет внутри нейросети кодироваться вектором из нулей и единицы (sic!). Например, буква А будет иметь индекс 1 и кодироваться вектором, где на первом месте единичка, а на остальных нули. Это называется one-hot encoding. Размерность каждого такого вектора равна размерности нашего алфавита токенов. И если для кириллического алфавита нам хватило бы 33 букв, то словари токенов из видосиков, которые я смотрел, имеют более внушительный размер: тысяч пятьдесят, например. Большие такие, длинные векторы нужны, короче.

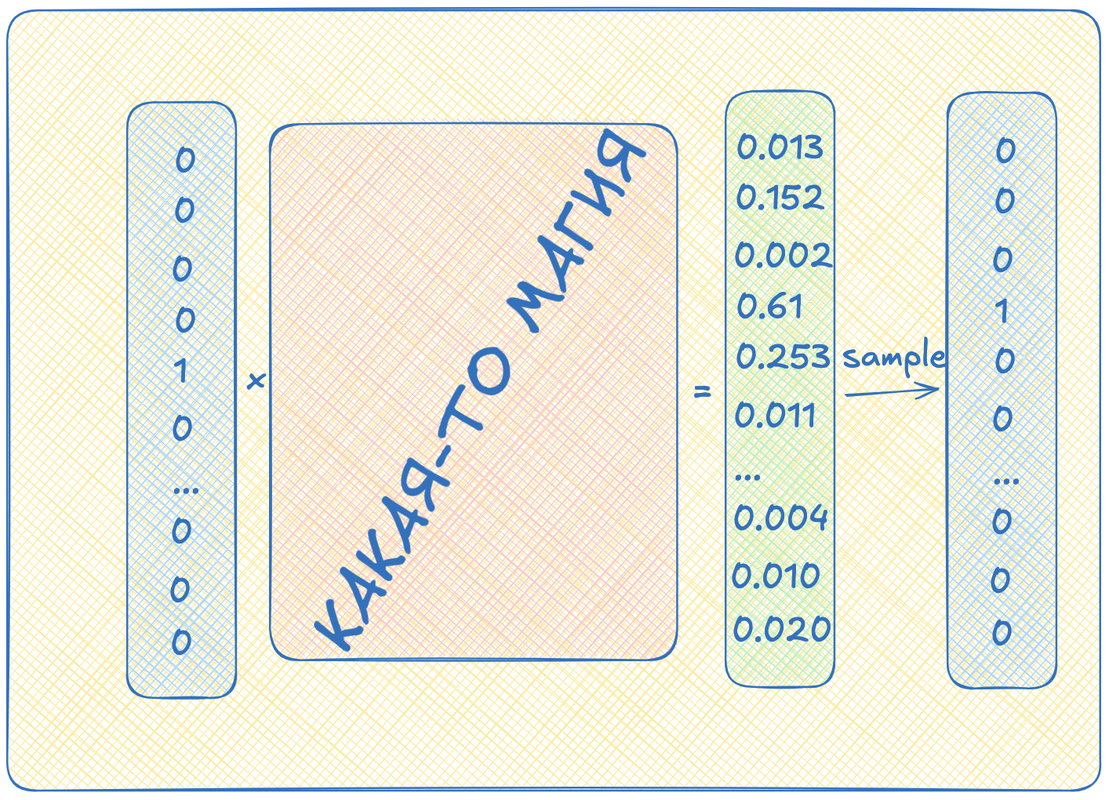
Следующий прикол состоит в том, что нейросеть нам будет выдавать вектор той же размерности, что мы ей дали на вход, но вот содержание там будет совсем другое. На выходе из нейронок мы будем получать вектор вещественных чисел от 0 до 1. Сумма всех чисел в векторе будет равна единице. Мы будем интерпретировать эти числа, как вероятности. Например, если на третьем месте в векторе будет число 0.65, мы будем считать, что с вероятностью 65% нам нужно выбрать число три. А если на пятом месте будет, например 0.03, то с вероятностью 3% будем выбирать число пять.

По сути, выход нейросети будет выдавать нам некоторое распределение, из которого мы будем делать выборку, состоящую из одного элемента. Вот получившееся, выбранное число мы и будем декодировать!

Нейросеть

Теперь настало время посмотреть, что такое сферическая нейросеть в вакууме. Для этого сначала посмотрим на один её узел -- перцептрон. Это штука, которая принимает вектор, собирает взвешенную сумму элементов этого вектора, отображает каким-нибудь образом эту сумму в отрезок от 0 до 1 и выдает результат нуружу. Это, кстати, называется "функция активации".

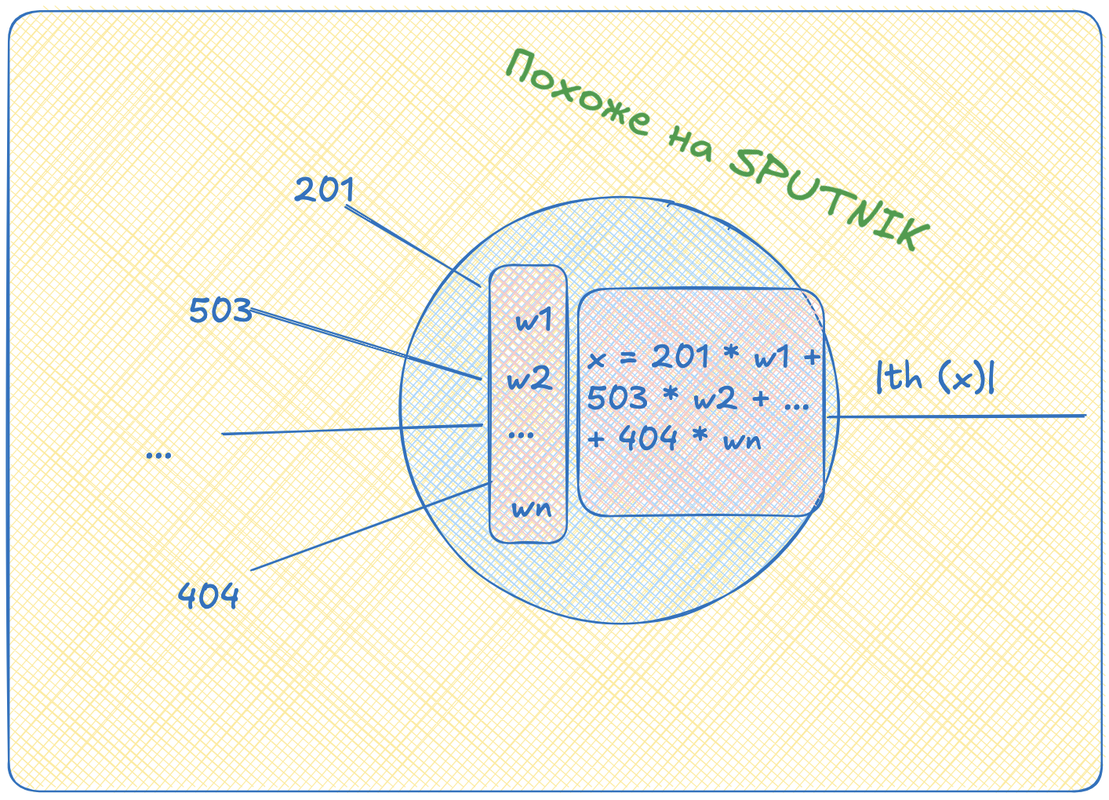
Здесь сразу стоит отослать вас вот к этому видосику

А теперь представьте, что мы такие круглешочки повтыкали друг в друга каким-то образом. Можно выход одного круглешочка воткнуть на вход нескольким другим, например.

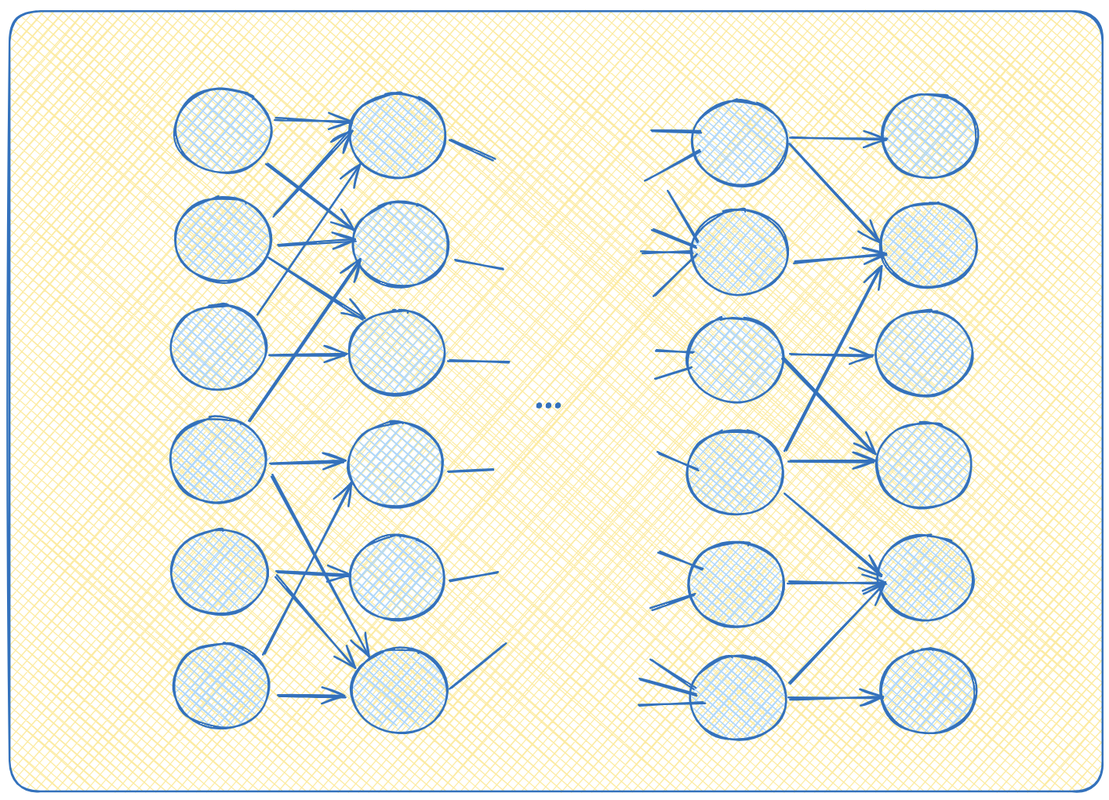
Давайте начнем думать, как появились значения на выходах самых правых перцептронов. Это какие-то th(w1*x1 + w2*x2 + ... + wn*xn). А сами иксы это в свою очередь что-то типа x1 = th (w'1*x'1 + w'2*x'2 + ... + w'n*x'n). И так далее. То есть довольно однообразные вложенные функции. Сильно и глубоко вложенные функции. Если разматывать этот клубок до самого конца, то можно в конце концов явно выписать уравнение: как вычисляются выходы, как функции от входов. Что-то типа y = th(w1*th(w'1*x1+...w'n*xn) + w2*th(....) + ...).

Можно заметить, что взвешенные суммы легко получаются при умножении вектора-строки на вектор-столбец. Ну или просто строки на столбец матрицы. И действительно, оказывается, что нейросеть описывается, как набор матриц, на которые мы умножаем входной вектор. А вот эти вот веса, w, это и есть параметры, веса нейросети. Именно они и записаны в матрицах. После всех этапов перемножений на выходе мы тоже получаем вектор. Вот и вся нейросеть. А я линейную алгебру на первом курсе учить не хотел!

Смотрим Андрея дальше

Обучение

Теперь от этой штуки очень удобно брать производную. Берем вот просто по каждой переменной на входе производную от вот этой длинной функции и получаем градиент. Причем, кто помнит из старших классов правила дифференцирования сложных функций (chain rule), тот может здесь увидеть, что у нас будет много одинаковых вычислений. Запоминая результаты таких повторяющихся вычислений, можно знатно сэкономить вычислительных ресурсов. Эта фишка называется back propagation и подробно с примерами нужно смотреть в этом видео. Есть более общий термин, differentiable programming.

Теперь давайте научим нейронку прогнозировать следующий токен по текущему. Возьмем кусок текста, в нем выберем токен для входа и запомним следующий за ним токен -- правильный выход.

Скормим входной токен в нейросеть, получим какой-то выход. Теперь сравним, насколько сильно этот выход отличается от того, что идет в тексте на самом деле. Вообще не обязательно понимать, как именно считать эту разницу, но для любителей статистики можно взять, например, (negative) log likelihood, а для любителей питона cross entropy (это примерно одно и то же).

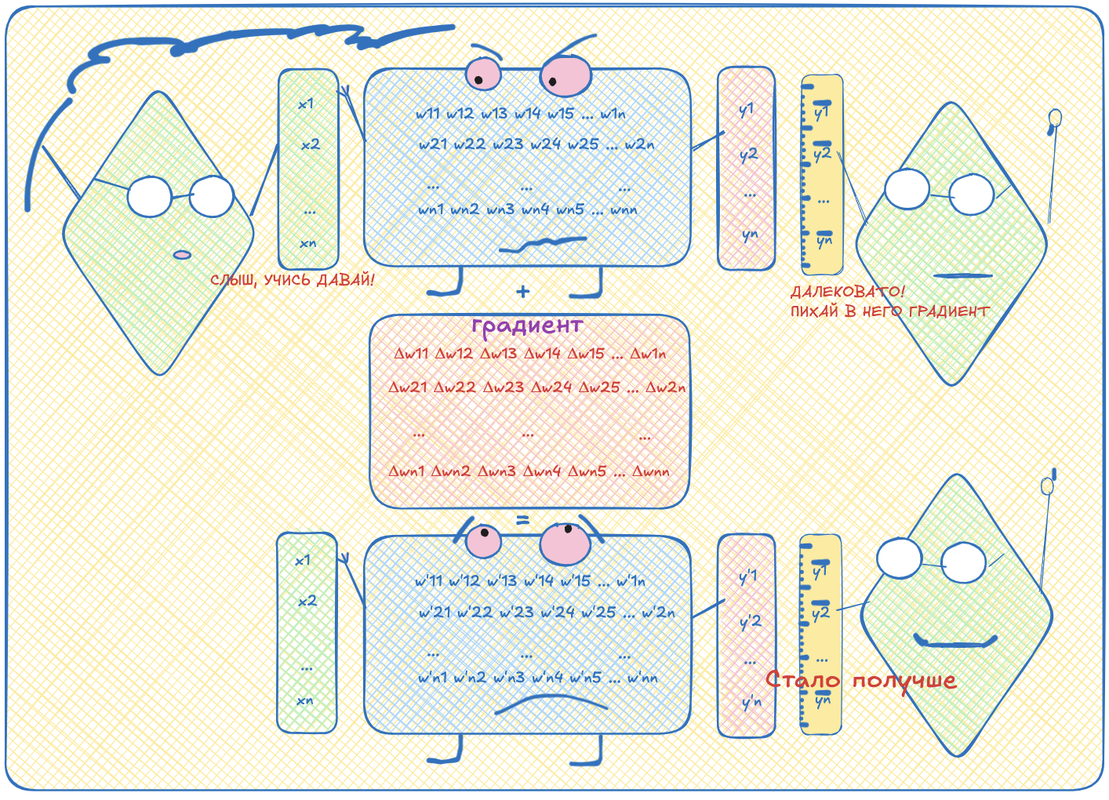
Вот эта разница -- это тоже математическая функция. Её тоже можно продифференцировать. Но давайте её дифференцировать не по переменным входа, а по переменным весам (которые w в формулах были). Тогда мы сможем изменять веса так, чтобы при прогоне нейронки с этими новыми весами, получаемое значение стало больше похоже на ожидаемое. Повторяя процедуру много раз, можно подогнать веся нейронки так, что она будет довольно точно прогнозировать, какой токен должен идти следующим. Статистически, конечно.

В целом, этого достаточно, чтобы примерно представлять себе, как работают нейросети вообще, и как их обучают. В общих чертах. Говорю же, я не эксперт, но даже после просмотра всего-то нескольких видосиков узнал десятки мест, где могут быть какие-то тонкости и различия. От функций активации и топологии сети до методов оптимизации и размерностей матриц внутри.

В следующей части расскажу про ембеддинги, кодирование контекста слова, смыслов слова. Потом про аттеншен, влияние слов друг на друга, форвардинг, норминг и всё такое. А в конце уже расскажу, почему ChatGPT подобные ассистенты это вообще-то не Т9 на стероидах.