Как найти кого угодно в социальных сетях используя графы и поиск в ширину

Немного определений

Граф - это топологическая модель, которая состоит из множества вершин и множества соединяющих их рёбер. При этом значение имеет только сам факт, какая вершина с какой соединена.

Очень многие задачи могут быть решены используя богатую библиотеку алгоритмов теории графов. Для этого достаточно лишь принять объекты за вершины, а связь между ними - за рёбра, после чего весь арсенал алгоритмов теории графов к вашим услугам: нахождение маршрута от одного объекта к другому, поиск связанных компонент, вычисление кратчайших путей, поиск сети максимального потока и многое другое.

В этой статье мы познакомимся с алгоритмом поиска в ширину, и применим его чтобы найти человека из ближайшего нашего окружения, который отвечает очень таки специфичным критериям поиска.

Storty: Вы крутой айтишник и хотите принять участие в Хакатоне "Лидеры цифровой трансформации", чтобы получить главный приз один миллион рублей за лучшее решение в кейсе, очевидно без классной и сплоченной команды это не сделать. Вам за короткий срок необходимо собрать команду и начать подготовку. Может начнем поиск среди друзей?

Начнем поиск в ширину

Вас зовут Петя и в некой социальной сети вы решаете опросить друзей не являются ли они программистами, и если являются, не хотят ли они в вашу команду?

Вы сразу понимаете, что поиск может затянуться и заводите журнал, в котором помечаете с кем ещё предстоит поговорить.

У вас два друга, вы записываете их в свой журнал и идете общаться с ними

Ваш журнал:

• Марина
• Катя

Вы начинаете с Марины..

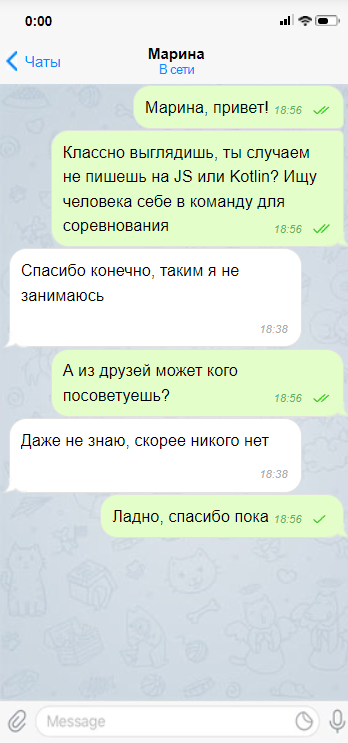
Марина, не тот кто вам нужен и вы идёте к Кате. Но перед тем как идти к Кате вы вычёркиваете Марину из Журнала

Ваш журнал:

• ̶М̶а̶р̶и̶н̶а̶
• Катя

Катя тоже вам не подошла, но поделилась контактами и вы можете продолжать поиск дальше, обратившись к её друзьям

Граф социальных связей теперь выглядит так

Егор и Джон являются для вас друзьями друзей. Для удобства будем называть такие связи - Связи второго уровня. А связь Пети с Катей и мариной связью первого уровня.

После разговора с Катей журнал выглядит Следующим образом

Ваш журнал:

• ̶М̶а̶р̶и̶н̶а̶
• ̶К̶а̶т̶я̶
• Егор
• Джон

Пишем Егору

Егор, нам не подходит, но он поделился своими контактами и мы их заносим в свой журнал в самый конец

• ̶М̶а̶р̶и̶н̶а̶
• ̶К̶а̶т̶я̶
• ̶Е̶г̶о̶р̶
• Джон
• Настя

Вам этот журнал ничего не напоминает? Первым пришел, последним ушел...
Правильно, это очередь.. Мы добавляем элементы в самый конец, а читаем с самого начала..

А вот так начинает выглядеть граф

Теперь пишем Джону и если окажется что он программист и хочет к нам в команду, мы на этом остановим поиск. Тем самым найдем контакт на втором уровне. Но если нет перейдем уже к анализу друзей 3-его уровня и так до самого конца пока такой человек не найдется... Этот алгоритм работает с любым размером графа, будь у каждого по 100 и более друзей, мы всё равно сможем найти именно ближащего айтишника по отношению к нам... Всё благодаря тому, что мы используем такую структуру данных как очередь..

Не верите? Попробуйте сами продолжить этот поиск, визуализируя всё это в голове или на бумаге..

Реализация алгоритма поиска в ширину на Kotlin

Листинг функции, она принимает идентификатор человека, от которого мы будем искать (в нашей примере мы искали ближайщую связь для Пети), и навык, например программирование на Kotlin

fun searchPersonWithNeedSkill(whoSearchId: String, skillName:String): PersonFullData? {
val searchQueue = ArrayDeque<String>()
val skillId = skillRepository.getSkillIdByName(skillName) ?: return null
val viewed = mutableSetOf<String>()
val personFriend1lvl = getPersonFriend(whoSearchId)
searchQueue.addAll(personFriend1lvl)
while (searchQueue.isNotEmpty()) {
val chekedPerson = searchQueue.removeFirst()
if (viewed.contains(chekedPerson)) continue
if(personHasSkill(chekedPerson, skillId )) {
return getPersonFullData(chekedPerson)
} else {
searchQueue.addAll(getPersonFriend(chekedPerson))
viewed.add(chekedPerson)
}
}
return null
}

Данная функция возвращает нам человека, который обладает заращиваемым навыком

Полный код программы тут https://github.com/TwoZeros/sosial-network

Если тема интересна и есть вопросы по реализации пишите.

Если ещё не читали Грокаем алгоритмы. Иллюстрированное пособие для программистов и любопытствующих | Бхаргава Адитья, то настоятельно рекомендую это сделать, там подробно рассматривается этот алгоритм .

Как задать Граф с помощью Kotlin я рассказ тут: https://www.youtube.com/watch?v=7cIMMPyHZCY