How to make a Hilbert space from scratch? | Part 2/2

So far, we have defined a metric space as a set that consists of at least a map that takes two elements from the set, gives back a non-negative element, and satisfies positive definiteness, symmetry, and triangle inequality properties. And we talked about sequences in the set that can be convergent or Cauchy. That results in a subclass of the metric space, which we call the complete metric space.

Now we can consider V, an F-vector space in which the scalars come from the field F (most of the time you can assume F as the real or complex fields). Then, we can use the metric mapping that we defined earlier to measure the distance between vectors in V. In the real world, we deal with a lot of vector spaces. You can easily think about the position of objects in classical mechanics. In this regard, we want to define a new function that measures the lengths of each vector in addition to measuring the distance between two elements.

Therefore, we can define a function ||.||: X → [0, +inf) and call it norm if, for every x and y belonging to V and every c belonging to F, we have:

1. ||x|| = 0 ←→ x = 0 
2. ||c.x|| = |c|.||x|| [absolutely homogenous]
3. ||x+y|| =< ||x|| + ||y|| [triangle inequality]

It is noteworthy that we can easily prove that every norm function can be easily transformed into a distance function with this definition: d(x,y) = ||x-y||. If the metric space (V, d) is a complete metric space, then we call the pair (V, ||.||) a Banach space, which lies at the intersection of vector spaces and complete metric spaces.

Now let's take it a step further. As well as measuring the length of each vector and the distance between two vectors, we want to define a new function that measures the direction between two vectors. This function takes two vectors from the vector space V as inputs and returns a non-negative real value as output, which can be denoted as <.,.>: V * V → [0, +inf), and we call it an inner product if for every x, y, and z in V and c in F we have:

1. <x,x> = 0 ←→ x=x [positive definite]
2. [(Conjugate) symmetry]

a) <x,y> = <y,x> if F = R

b) <x,y> = <y,x>* if F = C, where * denotes the complex conjugate.

3. [Linear in the second argument]

a) <x, y+z> = <x,y> + <x,z>

b) <x, c.y> = |c|. <x,y>

Now, if <.,.> is an inner product, we can prove that ||x|| = sqrt(<x,x>) defines a norm, and if the (V, ||.||) be a Banach space, then the (V, <.,.>) will be a Hilbert space. In addition, from the last paragraph, we knew that if (V, ||.||) is a Banach space, then (V, d(x,y)) = ||x-y|| = sqrt(<x,y>) had to be a complete metric space. So that’s it. Now we can really enjoy the below image that orders the mind.

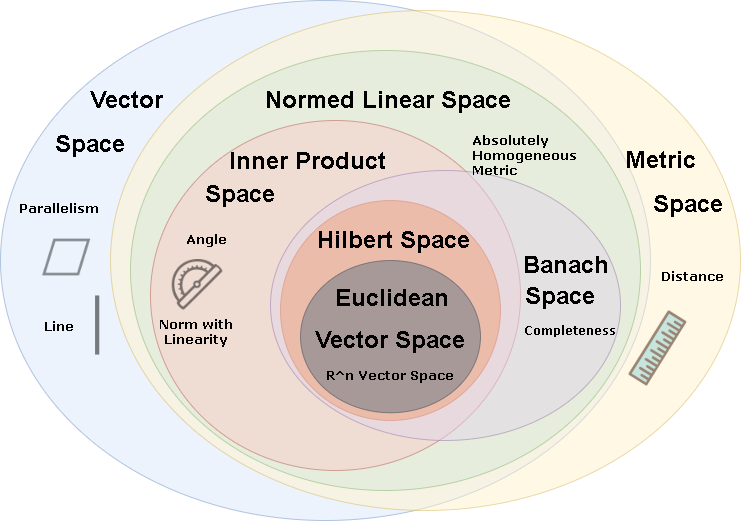
One can also prove that, with the definition of the inner product, sqrt(<x,x>) is a norm. And then, as we previously stated, we can also show why every norm can be transformed into a distance function. Now, you can remember the formulas that you had in high school for calculating the length of a vector or the distance between two vectors to verify the above formulation.

Please do not hesitate to tell me your opinion or comments about this blog, and don’t forget to share the message with your friends if you think it could be useful for them.