Hegel’s Dialectics

Next part 1

Hegel provides the most extensive, general account of his dialectical
method in Part I of his Encyclopaedia of Philosophical
Sciences, which is often called the Encyclopaedia Logic[EL]. The form or presentation of logic, he says, has three sides or
moments (EL §79). These sides are not parts of logic, but,
rather, moments of “every concept”, as well as “of
everything true in general” (EL Remark to §79; we will see
why Hegel thought dialectics is in everything in section 3). The first moment—the moment of the understanding—is the
moment of fixity, in which concepts or forms have a seemingly stable
definition or determination (EL §80).

The second moment—the “dialectical” (EL
§§79, 81) or “negatively rational” (EL
§79) moment—is the moment of instability. In this moment, a
one-sidedness or restrictedness (EL Remark to §81) in the
determination from the moment of understanding comes to the fore, and
the determination that was fixed in the first moment passes into its
opposite (EL §81). Hegel describes this process as a process of
“self-sublation” (EL §81). The English verb “to
sublate” translates Hegel’s technical use of the German
verb aufheben, which is a crucial concept in his dialectical
method. Hegel says that aufheben has a doubled meaning: it
means both to cancel (or negate) and to preserve at the same time (PhG
§113; SL-M 107; SL-dG 81–2; cf. EL the Addition to
§95). The moment of understanding sublates itselfbecause its own character or nature—its one-sidedness or
restrictedness—destabilizes its definition and leads it to pass
into its opposite. The dialectical moment thus involves a process of
self-sublation, or a process in which the determination from
the moment of understanding sublates itself, or both cancels
and preserves itself, as it pushes on to or passes into its
opposite.

The third moment—the “speculative” or
“positively rational” (EL §§79, 82)
moment—grasps the unity of the opposition between the first two
determinations, or is the positive result of the dissolution or
transition of those determinations (EL §82 and Remark to
§82). Here, Hegel rejects the traditional, reductio ad
absurdum argument, which says that when the premises of an
argument lead to a contradiction, then the premises must be discarded
altogether, leaving nothing. As Hegel suggests in the
Phenomenology, such an argument

is just the skepticism which only ever sees pure nothingness in its
result and abstracts from the fact that this nothingness is
specifically the nothingness of that from which it results.
(PhG-M §79)

Although the speculative moment negates the contradiction, it is a
determinate or defined nothingness because it is the result of a
specific process. There is something particular about the
determination in the moment of understanding—a specific
weakness, or some specific aspect that was ignored in its
one-sidedness or restrictedness—that leads it to fall apart in
the dialectical moment. The speculative moment has a definition,
determination or content because it grows out of and unifies the
particular character of those earlier determinations, or is “a
unity of distinct determinations” (EL Remark to
§82). The speculative moment is thus “truly not empty,
abstract nothing, but the negation of certain
determinations” (EL-GSH §82). When the result
“is taken as the result of that from which it emerges”,
Hegel says, then it is “in fact, the true result; in that case
it is itself a determinate nothingness, one which has a
content” (PhG-M §79). As he also puts it, “the result
is conceived as it is in truth, namely, as a determinatenegation [bestimmte Negation]; a new form has thereby
immediately arisen” (PhG-M §79). Or, as he says,
“[b]ecause the result, the negation, is a determinatenegation [bestimmte Negation], it has a
content” (SL-dG 33; cf. SL-M 54). Hegel’s claim
in both the Phenomenology and the Science of Logicthat his philosophy relies on a process of “determinatenegation [bestimmte Negation]” has sometimes led
scholars to describe his dialectics as a method or doctrine of
“determinate negation” (see entry on Hegel, section on Science of Logic; cf. Rosen 1982: 30; Stewart 1996, 2000: 41–3; Winfield 1990:
56).

There are several features of this account that Hegel thinks raise his
dialectical method above the arbitrariness of Plato’s dialectics
to the level of a genuine science. First, because the determinations
in the moment of understanding sublate themselves,
Hegel’s dialectics does not require some new idea to show up
arbitrarily. Instead, the movement to new determinations is driven by
the nature of the earlier determinations and so “comes about on
its own accord” (PhG-P §79). Indeed, for Hegel, the
movement is driven by necessity (see, e.g., EL Remarks to
§§12, 42, 81, 87, 88; PhG §79). The natures of the
determinations themselves drive or force them to pass into
their opposites. This sense of necessity—the idea that
the method involves being forced from earlier moments to later
ones—leads Hegel to regard his dialectics as a kind of
logic. As he says in the Phenomenology, the
method’s “proper exposition belongs to logic” (PhG-M
§48). Necessity—the sense of being driven or forced to
conclusions—is the hallmark of “logic” in Western
philosophy.

Second, because the form or determination that arises is the
result of the self-sublation of the determination from the
moment of understanding, there is no need for some new idea to show up
from the outside. Instead, the transition to the new determination or
form is necessitated by earlier moments and hence grows out of the
process itself. Unlike in Plato’s arbitrary dialectics,
then—which must wait around until some other idea comes in from
the outside—in Hegel’s dialectics “nothing
extraneous is introduced”, as he says (SL-M 54; cf. SL-dG 33).
His dialectics is driven by the nature, immanence or
“inwardness” of its own content (SL-M 54; cf. SL-dG 33;
cf. PR §31). As he puts it, dialectics is “the principle
through which alone immanent coherence and necessity enter
into the content of science” (EL-GSH Remark to §81).

Third, because later determinations “sublate” earlier
determinations, the earlier determinations are not completely
cancelled or negated. On the contrary, the earlier determinations are
preserved in the sense that they remain in effect within the
later determinations. When Being-for-itself, for instance, is
introduced in the logic as the first concept of ideality or
universality and is defined by embracing a set of
“something-others”, Being-for-itself replaces the
something-others as the new concept, but those something-others remain
active within the definition of the concept of Being-for-itself. The
something-others must continue to do the work of picking out
individual somethings before the concept of Being-for-itself can have
its own definition as the concept that gathers them up.
Being-for-itself replaces the something-others, but it also preserves
them, because its definition still requires them to do their work of
picking out individual somethings (EL §§95–6).

The concept of “apple”, for example, as a
Being-for-itself, would be defined by gathering up individual
“somethings” that are the same as one another (as apples).
Each individual apple can be what it is (as an apple) only in relation
to an “other” that is the same “something”
that it is (i.e., an apple). That is the one-sidedness or
restrictedness that leads each “something” to pass into
its “other” or opposite. The “somethings” are
thus both “something-others”. Moreover, their defining
processes lead to an endless process of passing back and forth into
one another: one “something” can be what it is (as an
apple) only in relation to another “something” that is the
same as it is, which, in turn, can be what it is (an apple) only in
relation to the other “something” that is the same as it
is, and so on, back and forth, endlessly (cf. EL §95). The
concept of “apple”, as a Being-for-itself, stops that
endless, passing-over process by embracing or including the individual
something-others (the apples) in its content. It grasps or captures
their character or quality as apples. But the
“something-others” must do their work of picking out and
separating those individual items (the apples) before the
concept of “apple”—as the Being-for-itself—can
gather them up for its own definition. We can picture the concept of
Being-for-itself like this:

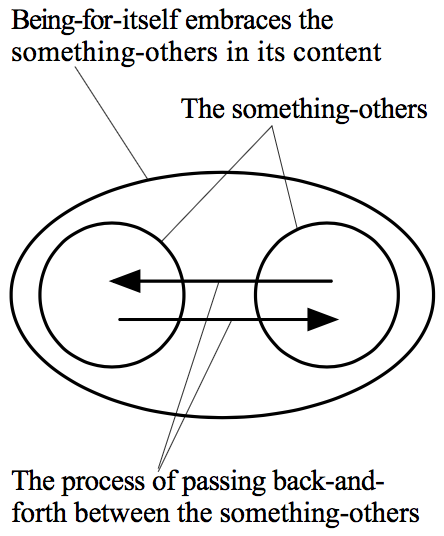
Figure 1

Later concepts thus replace, but also preserve, earlier concepts.

Fourth, later concepts both determine and also surpass the limits or
finitude of earlier concepts. Earlier determinations sublate
themselves—they pass into their others because of some
weakness, one-sidedness or restrictedness in their own definitions.
There are thus limitations in each of the determinations that lead
them to pass into their opposites. As Hegel says, “that is what
everything finite is: its own sublation” (EL-GSH Remark to
§81). Later determinations define the finiteness of the earlier
determinations. From the point of view of the concept of
Being-for-itself, for instance, the concept of a
“something-other” is limited or finite: although the
something-others are supposed to be the same as one another, the
character of their sameness (e.g., as apples) is captured only from
above, by the higher-level, more universal concept of
Being-for-itself. Being-for-itself reveals the limitations of the
concept of a “something-other”. It also rises above those
limitations, since it can do something that the concept of a
something-other cannot do. Dialectics thus allows us to get beyond the
finite to the universal. As Hegel puts it, “all genuine,
nonexternal elevation above the finite is to be found in this
principle [of dialectics]” (EL-GSH Remark to §81).

Fifth, because the determination in the speculative moment grasps the
unity of the first two moments, Hegel’s dialectical
method leads to concepts or forms that are increasingly comprehensive
and universal. As Hegel puts it, the result of the dialectical process

is a new concept but one higher and richer than the
preceding—richer because it negates or opposes the preceding and
therefore contains it, and it contains even more than that, for it is
the unity of itself and its opposite. (SL-dG 33; cf. SL-M 54)

Like Being-for-itself, later concepts are more universal because they
unify or are built out of earlier determinations, and include
those earlier determinations as part of their definitions. Indeed,
many other concepts or determinations can also be depicted as
literally surrounding earlier ones (cf. Maybee 2009: 73, 100, 112,
156, 193, 214, 221, 235, 458).

Finally, because the dialectical process leads to increasing
comprehensiveness and universality, it ultimately produces a complete
series, or drives “to completion” (SL-dG 33; cf. SL-M 54;
PhG §79). Dialectics drives to the “Absolute”, to use
Hegel’s term, which is the last, final, and completely
all-encompassing or unconditioned concept or form in the relevant
subject matter under discussion (logic, phenomenology, ethics/politics
and so on). The “Absolute” concept or form is
unconditioned because its definition or determination contains all the
other concepts or forms that were developed earlier in the dialectical
process for that subject matter. Moreover, because the process
develops necessarily and comprehensively through each concept, form or
determination, there are no determinations that are left out of the
process. There are therefore no left-over concepts or
forms—concepts or forms outside of the
“Absolute”—that might “condition” or
define it. The “Absolute” is thus unconditioned because it
contains all of the conditions in its content, and is not conditioned
by anything else outside of it. This Absolute is the highest concept
or form of universality for that subject matter. It is the thought or
concept of the whole conceptual system for the relevant subject
matter. We can picture the Absolute Idea (EL §236), for
instance—which is the “Absolute” for logic—as
an oval that is filled up with and surrounds numerous, embedded rings
of smaller ovals and circles, which represent all of the earlier and
less universal determinations from the logical development (cf. Maybee
2009: 30, 600):

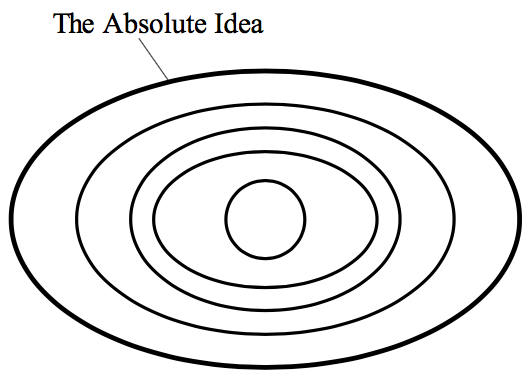
Figure 2

Since the “Absolute” concepts for each subject matter lead
into one another, when they are taken together, they constitute
Hegel’s entire philosophical system, which, as Hegel says,
“presents itself therefore as a circle of circles” (EL-GSH
§15). We can picture the entire system like this (cf. Maybee
2009: 29):

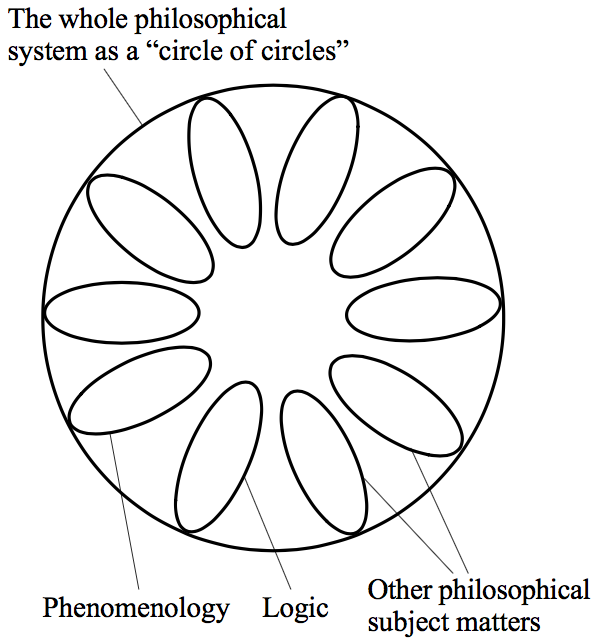
Figure 3

Together, Hegel believes, these characteristics make his dialectical
method genuinely scientific. As he says, “the dialectical
constitutes the moving soul of scientific progression” (EL-GSH
Remark to §81). He acknowledges that a description of the method
can be more or less complete and detailed, but because the method or
progression is driven only by the subject matter itself, this
dialectical method is the “only true method” (SL-M 54;
SL-dG 33).

So far, we have seen how Hegel describes his dialectical method, but
we have yet to see how we might read this method into the arguments he
offers in his works. Scholars often use the first three stages of the
logic as the “textbook example” (Forster 1993: 133) to
illustrate how Hegel’s dialectical method should be applied to
his arguments. The logic begins with the simple and immediate concept
of pure Being, which is said to illustrate the moment of the
understanding. We can think of Being here as a concept of pure
presence. It is not mediated by any other concept—or is not
defined in relation to any other concept—and so is undetermined
or has no further determination (EL §86; SL-M 82; SL-dG 59). It
asserts bare presence, but what that presence is like has no further
determination. Because the thought of pure Being is undetermined and
so is a pure abstraction, however, it is really no different from the
assertion of pure negation or the absolutely negative (EL §87).
It is therefore equally a Nothing (SL-M 82; SL-dG 59). Being’s
lack of determination thus leads it to sublate itself and pass into
the concept of Nothing (EL §87; SL-M 82; SL-dG 59), which
illustrates the dialectical moment.

But if we focus for a moment on the definitions of Being and Nothing
themselves, their definitions have the same content. Indeed, both are
undetermined, so they have the same kind of undefined content. The
only difference between them is “something merely
meant” (EL-GSH Remark to §87), namely, that Being is
an undefined content, taken as or meant to be presence, while Nothing
is an undefined content, taken as or meant to be absence. The third
concept of the logic—which is used to illustrate the speculative
moment—unifies the first two moments by capturing the positive
result of—or the conclusion that we can draw from—the
opposition between the first two moments. The concept of Becoming is
the thought of an undefined content, taken as presence (Being) and
then taken as absence (Nothing), or taken as absence (Nothing) and
then taken as presence (Being). To Become is to go from Being to
Nothing or from Nothing to Being, or is, as Hegel puts it, “the
immediate vanishing of the one in the other” (SL-M 83; cf. SL-dG
60). The contradiction between Being and Nothing thus is not a
reductio ad absurdum, or does not lead to the rejection of
both concepts and hence to nothingness—as Hegel had said
Plato’s dialectics does (SL-M 55–6; SL-dG
34–5)—but leads to a positive result, namely, to the
introduction of a new concept—the synthesis—which unifies
the two, earlier, opposed concepts.

We can also use the textbook Being-Nothing-Becoming example to
illustrate Hegel’s concept of aufheben (to sublate),
which, as we saw, means to cancel (or negate) and to preserve at the
same time. Hegel says that the concept of Becoming sublates the
concepts of Being and Nothing (SL-M 105; SL-dG 80). Becoming cancels
or negates Being and Nothing because it is a new concept that replaces
the earlier concepts; but it also preserves Being and Nothing because
it relies on those earlier concepts for its own definition. Indeed, it
is the first concrete concept in the logic. Unlike Being and Nothing,
which had no definition or determination as concepts themselves and so
were merely abstract (SL-M 82–3; SL-dG 59–60; cf. EL
Addition to §88), Becoming is a “determinate unity
in which there is both Being and Nothing” (SL-M 105;
cf. SL-dG 80). Becoming succeeds in having a definition or
determination because it is defined by, or piggy-backs on, the
concepts of Being and Nothing.

This “textbook” Being-Nothing-Becoming example is closely
connected to the traditional idea that Hegel’s dialectics
follows a thesis-antithesis-synthesis pattern, which, when applied to
the logic, means that one concept is introduced as a
“thesis” or positive concept, which then develops into a
second concept that negates or is opposed to the first or is its
“antithesis”, which in turn leads to a third concept, the
“synthesis”, that unifies the first two (see, e.g.,
McTaggert 1964 [1910]: 3–4; Mure 1950: 302; Stace, 1955 [1924]:
90–3, 125–6; Kosek 1972: 243; E. Harris 1983: 93–7;
Singer 1983: 77–79). Versions of this interpretation of
Hegel’s dialectics continue to have currency (e.g., Forster
1993: 131; Stewart 2000: 39, 55; Fritzman 2014: 3–5). On this
reading, Being is the positive moment or thesis, Nothing is the
negative moment or antithesis, and Becoming is the moment of
aufheben or synthesis—the concept that cancels and
preserves, or unifies and combines, Being and Nothing.

We must be careful, however, not to apply this textbook example too
dogmatically to the rest of Hegel’s logic or to his dialectical
method more generally (for a classic criticism of the
thesis-antithesis-synthesis reading of Hegel’s dialectics, see
Mueller 1958). There are other places where this general pattern might
describe some of the transitions from stage to stage, but there are
many more places where the development does not seem to fit this
pattern very well. One place where the pattern seems to hold, for
instance, is where the Measure (EL §107)—as the combination
of Quality and Quantity—transitions into the Measureless (EL
§107), which is opposed to it, which then in turn transitions
into Essence, which is the unity or combination of the two earlier
sides (EL §111). This series of transitions could be said to
follow the general pattern captured by the “textbook
example”: Measure would be the moment of the understanding or
thesis, the Measureless would be the dialectical moment or antithesis,
and Essence would be the speculative moment or synthesis that unifies
the two earlier moments. However, before the transition to Essence
takes place, the Measureless itself is redefined as a Measure (EL
§109)—undercutting a precise parallel with the textbook
Being-Nothing-Becoming example, since the transition from Measure to
Essence would not follow a Measure-Measureless-Essence pattern, but
rather a Measure-(Measureless?)-Measure-Essence pattern.

Other sections of Hegel’s philosophy do not fit the triadic,
textbook example of Being-Nothing-Becoming at all, as even
interpreters who have supported the traditional reading of
Hegel’s dialectics have noted. After using the
Being-Nothing-Becoming example to argue that Hegel’s dialectical
method consists of “triads” whose members “are
called the thesis, antithesis, synthesis” (Stace 1955 [1924]:
93), W.T. Stace, for instance, goes on to warn us that Hegel does not
succeed in applying this pattern throughout the philosophical system.
It is hard to see, Stace says, how the middle term of some of
Hegel’s triads are the opposites or antitheses of the first
term, “and there are even ‘triads’ which contain
four terms!” (Stace 1955 [1924]: 97). As a matter of fact, one
section of Hegel’s logic—the section on
Cognition—violates the thesis-antithesis-synthesis pattern
because it has only two sub-divisions, rather than three. “The
triad is incomplete”, Stace complains. “There is no third.
Hegel here abandons the triadic method. Nor is any explanation of his
having done so forthcoming” (Stace 1955 [1924]: 286; cf.
McTaggart 1964 [1910]: 292).

Interpreters have offered various solutions to the complaint that
Hegel’s dialectics sometimes seems to violate the triadic form.
Some scholars apply the triadic form fairly loosely across several
stages (e.g. Burbidge 1981: 43–5; Taylor 1975: 229–30).
Others have applied Hegel’s triadic method to whole sections of
his philosophy, rather than to individual stages. For G.R.G. Mure, for
instance, the section on Cognition fits neatly into a triadic,
thesis-antithesis-synthesis account of dialectics because the whole
section is itself the antithesis of the previous section of
Hegel’s logic, the section on Life (Mure 1950: 270). Mure argues
that Hegel’s triadic form is easier to discern the more broadly
we apply it. “The triadic form appears on many scales”, he
says, “and the larger the scale we consider the more obvious it
is” (Mure 1950: 302).

Scholars who interpret Hegel’s description of dialectics on a
smaller scale—as an account of how to get from stage to
stage—have also tried to explain why some sections seem to
violate the triadic form. J.N. Findlay, for instance—who, like
Stace, associates dialectics “with the triad, or with
triplicity”—argues that stages can fit into that
form in “more than one sense” (Findlay 1962: 66). The
first sense of triplicity echoes the textbook, Being-Nothing-Becoming
example. In a second sense, however, Findlay says, the dialectical
moment or “contradictory breakdown” is not itself a
separate stage, or “does not count as one of the stages”,
but is a transition between opposed, “but complementary”,
abstract stages that “are developed more or less
concurrently” (Findlay 1962: 66). This second sort of triplicity
could involve any number of stages: it “could readily have been
expanded into a quadruplicity, a quintuplicity and so forth”
(Findlay 1962: 66). Still, like Stace, he goes on to complain that
many of the transitions in Hegel’s philosophy do not seem to fit
the triadic pattern very well. In some triads, the second term is
“the direct and obvious contrary of the first”—as in
the case of Being and Nothing. In other cases, however, the opposition
is, as Findlay puts it, “of a much less extreme character”
(Findlay 1962: 69). In some triads, the third term obviously mediates
between the first two terms. In other cases, however, he says, the
third term is just one possible mediator or unity among other possible
ones; and, in yet other cases, “the reconciling functions of the
third member are not at all obvious” (Findlay 1962: 70).

Let us look more closely at one place where the “textbook
example” of Being-Nothing-Becoming does not seem to describe the
dialectical development of Hegel’s logic very well. In a later
stage of the logic, the concept of Purpose goes through several
iterations, from Abstract Purpose (EL §204), to Finite or
Immediate Purpose (EL §205), and then through several stages of a
syllogism (EL §206) to Realized Purpose (EL §210). Abstract
Purpose is the thought of any kind of purposiveness, where the purpose
has not been further determined or defined. It includes not just the
kinds of purposes that occur in consciousness, such as needs or
drives, but also the “internal purposiveness” or
teleological view proposed by the ancient Greek philosopher, Aristotle
(see entry on Aristotle; EL Remark to §204), according to which things in the world have
essences and aim to achieve (or have the purpose of living up to)
their essences. Finite Purpose is the moment in which an Abstract
Purpose begins to have a determination by fixing on some particular
material or content through which it will be realized (EL §205).
The Finite Purpose then goes through a process in which it, as the
Universality, comes to realize itself as the Purpose over the
particular material or content (and hence becomes Realized Purpose) by
pushing out into Particularity, then into Singularity (the syllogism
U-P-S), and ultimately into ‘out-thereness,’ or into
individual objects out there in the world (EL §210; cf. Maybee
2009: 466–493).

Hegel’s description of the development of Purpose does not seem
to fit the textbook Being-Nothing-Becoming example or the
thesis-antithesis-synthesis model. According to the example and model,
Abstract Purpose would be the moment of understanding or thesis,
Finite Purpose would be the dialectical moment or antithesis, and
Realized Purpose would be the speculative moment or synthesis.
Although Finite Purpose has a different determination from
Abstract Purpose (it refines the definition of Abstract Purpose), it
is hard to see how it would qualify as strictly “opposed”
to or as the “antithesis” of Abstract Purpose in the way
that Nothing is opposed to or is the antithesis of Being.

There is an answer, however, to the criticism that many of the
determinations are not “opposites” in a strict sense. The
German term that is translated as “opposite” in
Hegel’s description of the moments of dialectics (EL
§§81, 82)—entgegensetzen—has three root
words: setzen (“to posit or set”),
gegen, (“against”), and the prefix ent-,
which indicates that something has entered into a new state. The verb
entgegensetzen can therefore literally be translated as
“to set over against”. The
“engegengesetzte” into which determinations pass,
then, do not need to be the strict “opposites” of the
first, but can be determinations that are merely “set
against” or are different from the first ones. And the prefix
ent-, which suggests that the first determinations are put
into a new state, can be explained by Hegel’s claim that the
finite determinations from the moment of understanding sublate (cancel
but also preserve) themselves (EL §81): later determinations put
earlier determinations into a new state by preservingthem.

At the same time, there is a technical sense in which a later
determination would still be the “opposite” of the earlier
determination. Since the second determination is different from the
first one, it is the logical negation of the first one, or is
not-the-first-determination. If the first determination is
“e”, for instance, because the new determination is
different from that one, the new one is “not-e” (Kosek
1972: 240). Since Finite Purpose, for instance, has a definition or
determination that is different from the definition that Abstract
Purpose has, it is not-Abstract-Purpose, or is the negation
or opposite of Abstract Purpose in that sense. There is therefore a
technical, logical sense in which the second concept or form is the
“opposite” or negation of—or is
“not”—the first one—though, again, it need not
be the “opposite” of the first one in a strict sense.

Other problems remain, however. Because the concept of Realized
Purpose is defined through a syllogistic process, it is itself the
product of several stages of development (at least four, by my count,
if Realized Purpose counts as a separate determination), which would
seem to violate a triadic model. Moreover, the concept of Realized
Purpose does not, strictly speaking, seem to be the unity or
combination of Abstract Purpose and Finite Purpose. Realized Purpose
is the result of (and so unifies) the syllogistic process of Finite
Purpose, through which Finite Purpose focuses on and is realized in a
particular material or content. Realized Purpose thus seems to be a
development of Finite Purpose, rather than a unity or combination of
Abstract Purpose and Finite Purpose, in the way that Becoming can be
said to be the unity or combination of Being and Nothing.

These sorts of considerations have led some scholars to interpret
Hegel’s dialectics in a way that is implied by a more literal
reading of his claim, in the Encyclopaedia Logic, that the
three “sides” of the form of logic—namely, the
moment of understanding, the dialectical moment, and the speculative
moment—“are moments of each [or every;
jedes] logically-real, that is each [or every;
jedes] concept” (EL Remark to §79; this is an
alternative translation). The quotation suggests that each
concept goes through all three moments of the dialectical
process—a suggestion reinforced by Hegel’s claim, in the
Phenomenology, that the result of the process of determinate
negation is that “a new form has thereby immediately
arisen” (PhG-M §79). According to this interpretation, the
three “sides” are not three different concepts or forms
that are related to one another in a triad—as the textbook
Being-Nothing-Becoming example suggests—but rather different
momentary sides or “determinations” in the life, so to
speak, of each concept or form as it transitions to the next
one. The three moments thus involve only two concepts or forms: the
one that comes first, and the one that comes next (examples of
philosophers who interpret Hegel’s dialectics in this second way
include Maybee 2009; Priest 1989: 402; Rosen 2014: 122, 132; and
Winfield 1990: 56).

For the concept of Being, for example, its moment of understanding is
its moment of stability, in which it is asserted to be pure presence.
This determination is one-sided or restricted however, because, as we
saw, it ignores another aspect of Being’s definition, namely,
that Being has no content or determination, which is how Being is
defined in its dialectical moment. Being thus sublates itselfbecause the one-sidedness of its moment of understanding undermines
that determination and leads to the definition it has in the
dialectical moment. The speculative moment draws out the implications
of these moments: it asserts that Being (as pure presence) implies
nothing. It is also the “unity of the determinations in their
comparison [Entgegensetzung]” (EL §82; alternative
translation): since it captures a process from one to the other, it
includes Being’s moment of understanding (as pure presence) and
dialectical moment (as nothing or undetermined), but also
compares those two determinations, or sets (-setzen)
them up against (-gegen) each other. It even puts Being into
a new state (as the prefix ent- suggests) because the next
concept, Nothing, will sublate (cancel and preserve)
Being.

The concept of Nothing also has all three moments. When it is asserted
to be the speculative result of the concept of Being, it has its
moment of understanding or stability: it is Nothing, defined as pure
absence, as the absence of determination. But Nothing’s moment
of understanding is also one-sided or restricted: like Being, Nothing
is also an undefined content, which is its determination in its
dialectical moment. Nothing thus sublates itself: since it is
an undefined content, it is not pure absence after all, but
has the same presence that Being did. It is presentas an undefined content. Nothing thus sublatesBeing: it replaces (cancels) Being, but also preserves Being insofar
as it has the same definition (as an undefined content) and presence
that Being had. We can picture Being and Nothing like this (the
circles have dashed outlines to indicate that, as concepts, they are
each undefined; cf. Maybee 2009: 51):

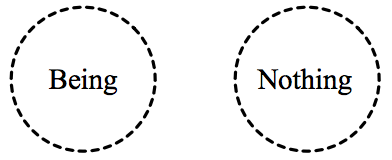
Figure 4

In its speculative moment, then, Nothing implies presence or Being,
which is the “unity of the determinations in their comparison
[Entgegensetzung]” (EL §82; alternative
translation), since it both includes but—as a process
from one to the other—also compares the two earlier
determinations of Nothing, first, as pure absence and, second, as just
as much presence.

The dialectical process is driven to the next concept or
form—Becoming—not by a triadic,
thesis-antithesis-synthesis pattern, but by the one-sidedness of
Nothing—which leads Nothing to sublate itself—and by the
implications of the process so far. Since Being and Nothing have each
been exhaustively analyzed as separate concepts, and since they are
the only concepts in play, there is only one way for the dialectical
process to move forward: whatever concept comes next will have to take
account of both Being and Nothing at the same time. Moreover, the
process revealed that an undefined content taken to be presence (i.e.,
Being) implies Nothing (or absence), and that an undefined content
taken to be absence (i.e., Nothing) implies presence (i.e., Being).
The next concept, then, takes Being and Nothing together and draws out
those implications—namely, that Being implies Nothing, and that
Nothing implies Being. It is therefore Becoming, defined as two
separate processes: one in which Being becomes Nothing, and one in
which Nothing becomes Being. We can picture Becoming this way (cf.
Maybee 2009: 53):

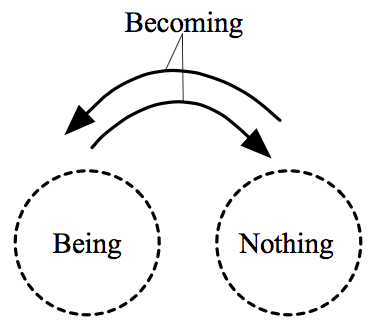
Figure 5

In a similar way, a one-sidedness or restrictedness in the
determination of Finite Purpose together with the implications of
earlier stages leads to Realized Purpose. In its moment of
understanding, Finite Purpose particularizes into (or presents) its
content as “something-presupposed” or as a
pre-given object (EL §205). I go to a restaurant for the purpose
of having dinner, for instance, and order a salad. My purpose of
having dinner particularizes as a pre-given object—the salad.
But this object or particularity—e.g. the salad—is
“inwardly reflected” (EL §205): it has its own
content—developed in earlier stages—which the definition
of Finite Purpose ignores. We can picture Finite Purpose this way:

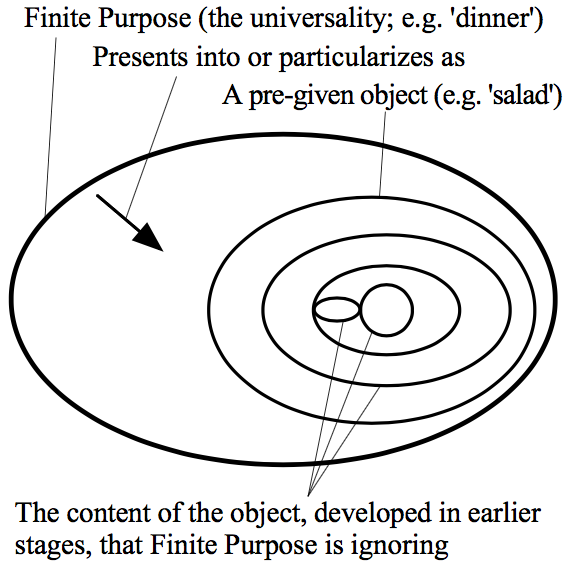
Figure 6

In the dialectical moment, Finite Purpose is determined by the
previously ignored content, or by that other content. The
one-sidedness of Finite Purpose requires the dialectical process to
continue through a series of syllogisms that determines Finite Purpose
in relation to the ignored content. The first syllogism links the
Finite Purpose to the first layer of content in the object: the
Purpose or universality (e.g., dinner) goes through the particularity
(e.g., the salad) to its content, the singularity (e.g., lettuce as a
type of thing)—the syllogism U-P-S (EL §206). But the
particularity (e.g., the salad) is itself a universality or purpose,
“which at the same time is a syllogism within itself [in
sich]” (EL Remark to §208; alternative translation),
in relation to its own content. The salad is a universality/purpose
that particularizes as lettuce (as a type of thing) and has its
singularity in this lettuce here—a second syllogism, U-P-S.
Thus, the first singularity (e.g., “lettuce” as a type of
thing)—which, in this second syllogism, is the particularity or
P—“judges” (EL §207) or asserts
that “U is S”: it says that
“lettuce” as a universality (U) or type of thing is
a singularity (S), or is “this lettuce here”, for
instance. This new singularity (e.g. “this lettuce here”)
is itself a combination of subjectivity and objectivity (EL
§207): it is an Inner or identifying concept
(“lettuce”) that is in a mutually-defining relationship
(the circular arrow) with an Outer or out-thereness (“this
here”) as its content. In the speculative moment, Finite Purpose
is determined by the whole process of development from the moment of
understanding—when it is defined by particularizing into a
pre-given object with a content that it ignores—to its
dialectical moment—when it is also defined by the previously
ignored content. We can picture the speculative moment of Finite
Purpose this way:

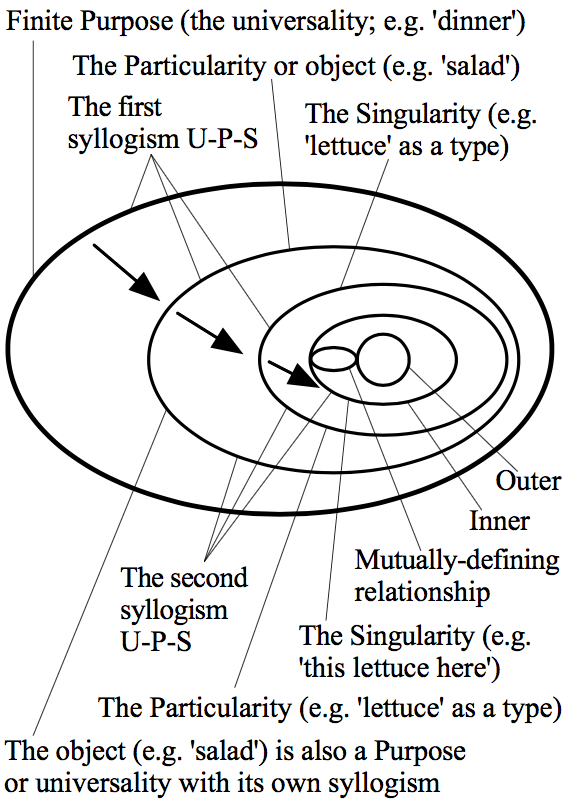
Figure 7

Finite Purpose’s speculative moment leads to Realized Purpose.
As soon as Finite Purpose presents all the content, there is a return
process (a series of return arrows) that establishes each layer and
redefines Finite Purpose as Realized Purpose. The presence of
“this lettuce here” establishes the actuality of
“lettuce” as a type of thing (an Actuality is a concept
that captures a mutually-defining relationship between an Inner and an
Outer [EL §142]), which establishes the “salad”,
which establishes “dinner” as the Realized Purpose over
the whole process. We can picture Realized Purpose this way:

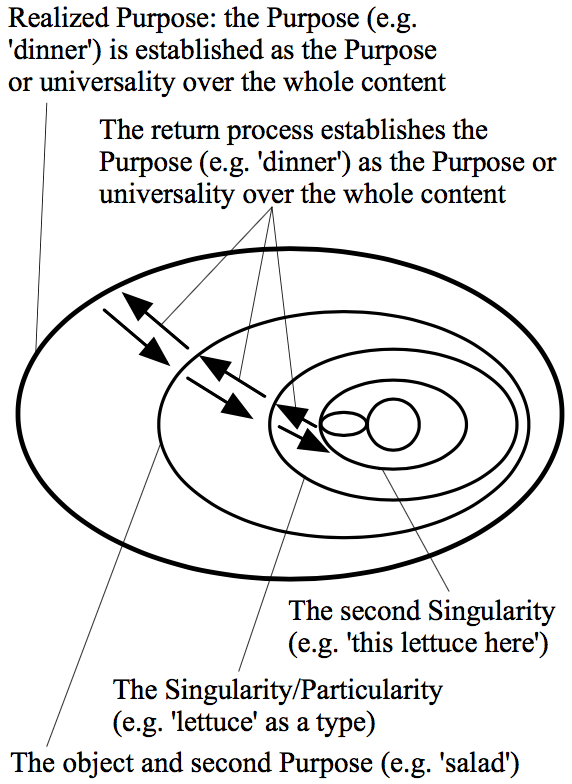
Figure 8

If Hegel’s account of dialectics is a general description of the
life of each concept or form, then any section can include as many or
as few stages as the development requires. Instead of trying to
squeeze the stages into a triadic form (cf. Solomon 1983: 22)—a
technique Hegel himself rejects (PhG §50; cf. section 3)—we can see the process as driven by each determination on its own
account: what it succeeds in grasping (which allows it to be stable,
for a moment of understanding), what it fails to grasp or capture (in
its dialectical moment), and how it leads (in its speculative moment)
to a new concept or form that tries to correct for the one-sidedness
of the moment of understanding. This sort of process might reveal a
kind of argument that, as Hegel had promised, might produce a
comprehensive and exhaustive exploration of every concept, form or
determination in each subject matter, as well as raise dialectics
above a haphazard analysis of various philosophical views to the level
of a genuine science.

We can begin to see why Hegel was motivated to use a dialectical
method by examining the project he set for himself, particularly in
relation to the work of David Hume and Immanuel Kant (see entries on Hume and Kant). Hume had argued against what we can think of as the naïve view
of how we come to have scientific knowledge. According to the
naïve view, we gain knowledge of the world by using our senses to
pull the world into our heads, so to speak. Although we may have to
use careful observations and do experiments, our knowledge of the
world is basically a mirror or copy of what the world is like. Hume
argued, however, that naïve science’s claim that our
knowledge corresponds to or copies what the world is like does not
work. Take the scientific concept of cause, for instance. According to
that concept of cause, to say that one event causes another is to say
that there is a necessary connection between the first event (the
cause) and the second event (the effect), such that, when the first
event happens, the second event must also happen. According to
naïve science, when we claim (or know) that some event
causes some other event, our claim mirrors or copies what the
world is like. It follows that the necessary, causal connection
between the two events must itself be out there in the world. However,
Hume argued, we never observe any such necessary causal connection in
our experience of the world, nor can we infer that one exists based on
our reasoning (see Hume’s A Treatise of Human Nature,
Book I, Part III, Section II; Enquiry Concerning Human
Understanding, Section VII, Part I). There is nothing in the
world itself that our idea of cause mirrors or copies.

Kant thought Hume’s argument led to an unacceptable, skeptical
conclusion, and he rejected Hume’s own solution to the
skepticism (see Kant’s Critique of Pure Reason, B5,
B19–20). Hume suggested that our idea of causal necessity is
grounded merely in custom or habit, since it is generated by our own
imaginations after repeated observations of one sort of event
following another sort of event (see Hume’s A Treatise of
Human Nature, Book I, Section VI; Hegel also rejected
Hume’s solution, see EL §39). For Kant, science and
knowledge should be grounded in reason, and he proposed a solution
that aimed to reestablish the connection between reason and knowledge
that was broken by Hume’s skeptical argument. Kant’s
solution involved proposing a Copernican revolution in philosophy
(Critique of Pure Reason, Bxvi). Nicholas Copernicus was the
Polish astronomer who said that the earth revolves around the sun,
rather than the other way around. Kant proposed a similar solution to
Hume’s skepticism. Naïve science assumes that our knowledge
revolves around what the world is like, but, Hume’s criticism
argued, this view entails that we cannot then have knowledge of
scientific causes through reason. We can reestablish a connection
between reason and knowledge, however, Kant suggested, if we
say—not that knowledge revolves around what the world is
like—but that knowledge revolves around what we are
like. For the purposes of our knowledge, Kant said, we do not
revolve around the world—the world revolves around us. Because
we are rational creatures, we share a cognitive structure with one
another that regularizes our experiences of the world. This
intersubjectively shared structure of rationality—and not the
world itself—grounds our knowledge.

However, Kant’s solution to Hume’s skepticism led to a
skeptical conclusion of its own that Hegel rejected. While the
intersubjectively shared structure of our reason might allow us to
have knowledge of the world from our perspective, so to speak, we
cannot get outside of our mental, rational structures to see what the
world might be like in itself. As Kant had to admit, according to his
theory, there is still a world in itself or
“Thing-in-itself” (Ding an sich) about which we
can know nothing (see, e.g., Critique of Pure Reason,
Bxxv–xxvi). Hegel rejected Kant’s skeptical conclusion
that we can know nothing about the world- or Thing-in-itself, and he
intended his own philosophy to be a response to this view (see, e.g.,
EL §44 and the Remark to §44).

How did Hegel respond to Kant’s skepticism—especially
since Hegel accepted Kant’s Copernican revolution, or
Kant’s claim that we have knowledge of the world because of what
we are like, because of our reason? How, for Hegel, can we get out of
our heads to see the world as it is in itself? Hegel’s answer is
very close to the ancient Greek philosopher Aristotle’s response
to Plato. Plato argued that we have knowledge of the world only
through the Forms. The Forms are perfectly universal, rational
concepts or ideas. Because the world is imperfect, however, Plato
exiled the Forms to their own realm. Although things in the world get
their definitions by participating in the Forms, those things are, at
best, imperfect copies of the universal Forms (see, e.g.,
Parmenides 131–135a). The Forms are therefore not in
this world, but in a separate realm of their own. Aristotle argued,
however, that the world is knowable not because things in the world
are imperfect copies of the Forms, but because the Forms are in things
themselves as the defining essences of those things (see, e.g., De
Anima [On the Soul], Book I, Chapter 1
[403a26–403b18]; Metaphysics, Book VII, Chapter 6
[1031b6–1032a5] and Chapter 8 [1033b20–1034a8]).

In a similar way, Hegel’s answer to Kant is that we can get out
of our heads to see what the world is like in itself—and hence
can have knowledge of the world in itself—because the very same
rationality or reason that is in our heads is in the world
itself. As Hegel apparently put it in a lecture, the opposition
or antithesis between the subjective and objective disappears by
saying, as the Ancients did,

that nous governs the world, or by our own saying that there
is reason in the world, by which we mean that reason is the soul of
the world, inhabits it, and is immanent in it, as it own, innermost
nature, its universal. (EL-GSH Addition 1 to §24)

Hegel used an example familiar from Aristotle’s work to
illustrate this view:

“to be an animal”, the kind considered as the universal,
pertains to the determinate animal and constitutes its determinate
essentiality. If we were to deprive a dog of its animality we could
not say what it is. (EL-GSH Addition 1 to §24; cf. SL-dG
16–17, SL-M 36-37)

Kant’s mistake, then, was that he regarded reason or rationality
as only in our heads, Hegel suggests (EL §§43–44),
rather than in both us and the world itself (see also below in this
section and section 4). We can use our reason to have knowledge of the world because the very
same reason that is in us, is in the world itself as it own defining
principle. The rationality or reason in the world makes reality
understandable, and that is why we can have knowledge of, or can
understand, reality with our rationality. Dialectics—which is
Hegel’s account of reason—characterizes not only logic,
but also “everything true in general” (EL Remark to
§79).

But why does Hegel come to define reason in terms of dialectics, and
hence adopt a dialectical method? We can begin to see what drove Hegel
to adopt a dialectical method by returning once again to Plato’s
philosophy. Plato argued that we can have knowledge of the world only
by grasping the Forms, which are perfectly universal, rational
concepts or ideas. Because things in the world are so imperfect,
however, Plato concluded that the Forms are not in this world, but in
a realm of their own. After all, if a human being were perfectly
beautiful, for instance, then he or she would never become
not-beautiful. But human beings change, get old, and die, and so can
be, at best, imperfect copies of the Form of beauty—though they
get whatever beauty they have by participating in that Form. Moreover,
for Plato, things in the world are such imperfect copies that we
cannot gain knowledge of the Forms by studying things in the world,
but only through reason, that is, only by using our rationality to
access the separate realm of the Forms (as Plato argued in the
well-known parable of the cave; Republic, Book 7,
514–516b).

Notice, however, that Plato’s conclusion that the Forms cannot
be in this world and so must be exiled to a separate realm rests on
two claims. First, it rests on the claim that the world is an
imperfect and messy place—a claim that is hard to deny. But it
also rests on the assumption that the Forms—the universal,
rational concepts or ideas of reason itself—are static and
fixed, and so cannot grasp the messiness within the imperfect world.
Hegel is able to link reason back to our messy world by changing the
definition of reason. Instead of saying that reason consists of static
universals, concepts or ideas, Hegel says that the universal concepts
or forms are themselves messy. Against Plato, Hegel’s
dialectical method allows him to argue that universal concepts can
“overgrasp” (from the German verb
übergreifen) the messy, dialectical nature of the world
because they, themselves, are dialectical. Moreover, because
later concepts build on or sublate (cancel, but also preserve) earlier
concepts, the later, more universal concepts grasp the dialectical
processes of earlier concepts. As a result, higher-level concepts can
grasp not only the dialectical nature of earlier concepts or forms,
but also the dialectical processes that make the world itself a messy
place. The highest definition of the concept of beauty, for instance,
would not take beauty to be fixed and static, but would include within
it the dialectical nature or finiteness of beauty, the idea that
beauty becomes, on its own account, not-beauty. This dialectical
understanding of the concept of beauty can then overgrasp the
dialectical and finite nature of beauty in the world, and hence the
truth that, in the world, beautiful things themselves become
not-beautiful, or might be beautiful in one respect and not another.
Similarly, the highest determination of the concept of
“tree” will include within its definition the dialectical
process of development and change from seed to sapling to tree. As
Hegel says, dialectics is “the principle of all natural and
spiritual life” (SL-M 56; SL-dG 35), or “the moving soul
of scientific progression” (EL §81). Dialectics is what
drives the development of both reason as well as of things in the
world. A dialectical reason can overgrasp a dialectical world.

Two further journeys into the history of philosophy will help to show
why Hegel chose dialectics as his method of argument. As we saw, Hegel
argues against Kant’s skepticism by suggesting that reason is
not only in our heads, but in the world itself. To show that reason is
in the world itself, however, Hegel has to show that reason can be
what it is without us human beings to help it. He has to show that
reason can develop on its own, and does not need us to do the
developing for it (at least for those things in the world that are not
human-created). As we saw (cf. section 1), central to Hegel’s dialectics is the idea that concepts or
forms develop on their own because they “self-sublate”, or
sublate (cancel and preserve) themselves, and so pass into
subsequent concepts or forms on their own accounts, because of their
own, dialectical natures. Thus reason, as it were, drives itself, and
hence does not need our heads to develop it. Hegel needs an account of
self-driving reason to get beyond Kant’s skepticism.

Ironically, Hegel derives the basic outlines of his account of
self-driving reason from Kant. Kant divided human rationality into two
faculties: the faculty of the understanding and the faculty of reason.
The understanding uses concepts to organize and regularize our
experiences of the world. Reason’s job is to coordinate the
concepts and categories of the understanding by developing a
completely unified, conceptual system, and it does this work, Kant
thought, on its own, independently of how those concepts might apply
to the world. Reason coordinates the concepts of the understanding by
following out necessary chains of syllogisms to produce concepts that
achieve higher and higher levels of conceptual unity. Indeed, this
process will lead reason to produce its own transcendental ideas, or
concepts that go beyond the world of experience. Kant calls this
necessary, concept-creating reason “speculative” reason
(cf. Critique of Pure Reason, Bxx–xxi, A327/B384).
Reason creates its own concepts or ideas—it
“speculates”—by generating new and increasingly
comprehensive concepts of its own, independently of the understanding.
In the end, Kant thought, reason will follow out such chains of
syllogisms until it develops completely comprehensive or unconditioned
universals—universals that contain all of the conditions or all
of the less-comprehensive concepts that help to define them. As we saw
(cf. section 1), Hegel’s dialectics adopts Kant’s notion of a self-driving
and concept-creating “speculative” reason, as well as
Kant’s idea that reason aims toward unconditioned universality
or absolute concepts.

Next part 1