Happy Number

https://leetcode.com/problems/happy-number/

Write an algorithm to determine if a number n is happy.

A happy number is a number defined by the following process:

• Starting with any positive integer, replace the number by the sum of the squares of its digits.
• Repeat the process until the number equals 1 (where it will stay), or it loops endlessly in a cycle which does not include 1.
• Those numbers for which this process ends in 1 are happy.

Return true if n is a happy number, and false if not.

Example 1:

Input: n = 19
Output: true
Explanation:
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1

Example 2:

Input: n = 2
Output: false

Solution:

Today we start with a code for this task, and then I will explain it to you:

  public boolean isHappy(int n) {
    int slowRunner = n;
    int fastRunner = getNext(n);
    while (fastRunner != 1 && slowRunner != fastRunner) {
      slowRunner = getNext(slowRunner);
      fastRunner = getNext(getNext(fastRunner));
    }
    return fastRunner == 1;
  }
   
  private int getNext(int n){
    int sum = 0;
    while(n > 0) {
      int rest = n % 10;
      n /= 10;
      sum += rest * rest;
    }
    return sum;
  }

Here we use the popular pattern "two pointers". But wait, why? How it can help us?

I cannot stand algo problems like this one, but... you see, sometimes we should handle with it.

Let's start with n = 7. Next number will be 7*7 = 49. Then 4*4 + 9*9 = 97. Then will be 130 and 10 --> 1.

In another example n = 116, and we have a situation like this:

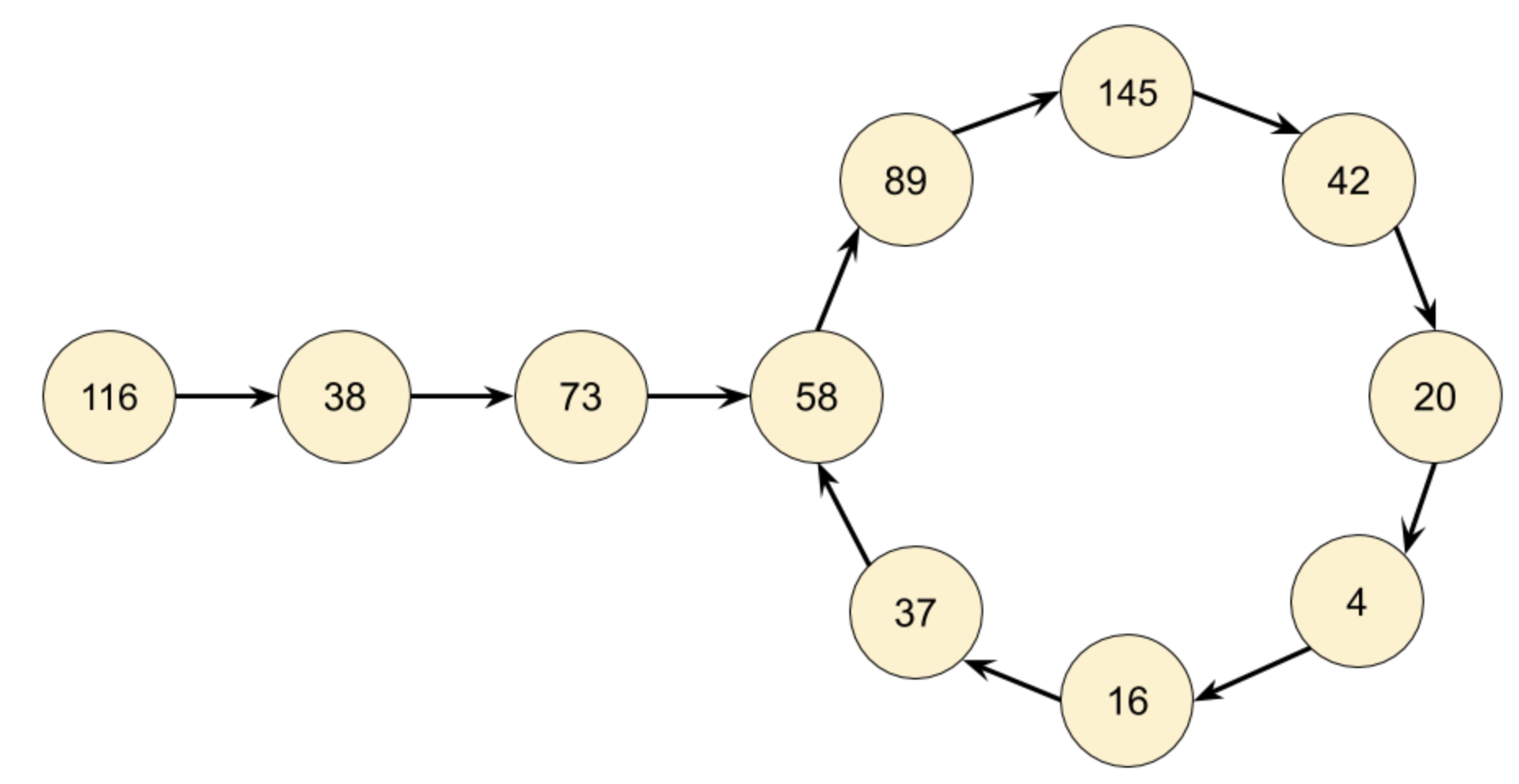
Based on our exploration so far, we'd expect continually following links to end in one of three ways.

1. It eventually gets to 1
2. It eventually gets stuck in a cycle.
3. It keeps going higher and higher, up towards infinity.

But is it possible to go infinitely? That 3rd option sounds really annoying to detect and handle. How would we even know that it is going to continue going up, rather than eventually going back down, possibly to 1?

1? Luckily, it turns out we don't need to worry about it. Think carefully about what the largest next number we could get for each number of digits is.

For a number with 3 digits, it's impossible for it to ever go larger than 243. This means it will have to either get stuck in a cycle below 243 or go down to 1.

Numbers with 4 or more digits will always lose a digit at each step until they are down to 3 digits. So we know that at worst, the algorithm might cycle around all the numbers under 243 and then go back to one it's already been to (a cycle) or goes to 1

1. But it won't go on indefinitely, allowing us to rule out the 3rd option.

Even though you don't need to handle the 3rd case in the code, you still need to understand why it can never happen, so that you can justify why you didn't handle it.

And then in getNext method, we should iteratively calculate the next number and that is it =) Enjoy.