Хакер - Цифровая электроника с самого начала. Изучаем сумматор и собираем его на макетной плате
hacker_frei
prostorosty
Содержание статьи
- Обработка чисел
- Двоичная система
- Перевод чисел из двоичной системы в десятичную и обратно
- Сложение
- Вычитание
- Умножение
- Арифметико-логические устройства
- Сумматор
- Универсальный сумматор-вычитатель
- Умножители
- Переходим к АЛУ
- Собираем АЛУ
- Однобитный полный сумматор
- Двухбитный сумматор
- Универсальный сумматор-вычитатель
- Выводы
Современные компьютеры способны совершать миллионы миллиардов операций за секунду. Среди самых базовых операций — математические. Чтобы понять, как именно компьютер их выполняет, мы сегодня обсудим устройство сумматора и арифметико‑логических устройств на его основе.
ОБРАБОТКА ЧИСЕЛ
Основная работа любого микропроцессора — это обработка чисел. А уже на ее основе совершаются другие, более сложные операции.
Цифровая электроника с самого начала
В своих прошлых статьях я рассказывал о двоичной системе счисления, алгебре логики и логических вентилях, электронных компонентах, микросхемах и многом другом интересном и полезном. Рекомендую ознакомиться, особенно если в этой статье встретятся непонятные вещи.
- Цифровая электроника с самого начала. Собираем схемы на MOSFET-транзисторах
- Бунт многоножек. Собираем устройство с интегральными микросхемами
В основе работы компьютера лежит арифметико‑логическое устройство (АЛУ). Чтобы понять, как оно работает, давай разберем принцип, который позволяет компьютеру совершать операции. Но сначала я подробнее расскажу о самой двоичной системе.
ДВОИЧНАЯ СИСТЕМА
Думаю, ты уже имеешь некоторое представление о двоичном счислении. Все числа в двоичной системе состоят из двух цифр — нуля и единицы. Внутри компьютер использует ее для всех операций, даже если работает с десятичными или шестнадцатеричными числами.
Перевод чисел из двоичной системы в десятичную и обратно
Переводить числа из одной системы в другую проще всего при помощи калькулятора, но для нас сейчас важно знать, как это делается, по шагам.
Число в десятичной системе счисления можно представить в виде суммы его цифр, помноженных на десять в степени разряда числа — от самого правого, которому соответствует 10 в нулевой степени, к самому левому, при том что степень каждый раз возрастает на единицу. Например:
389 = 3 ∙ 10² + 8 ∙ 10¹ + 9 · 10⁰ = 300 + 80 + 9
Точно так же можно раскладывать двоичные числа, только каждый разряд (самая правая цифра считается самым младшим разрядом) умножается не на степень десяти, а на степень двойки. В итоге мы получим число в десятичной системе. В качестве примера переведем число 1101 из двоичной в десятичную:
1101 = 1 ∙ 2³ + 1 · 2² + 0 · 2¹ + 1 · 2⁰ = 8 + 4 + 0 + 1 = 13
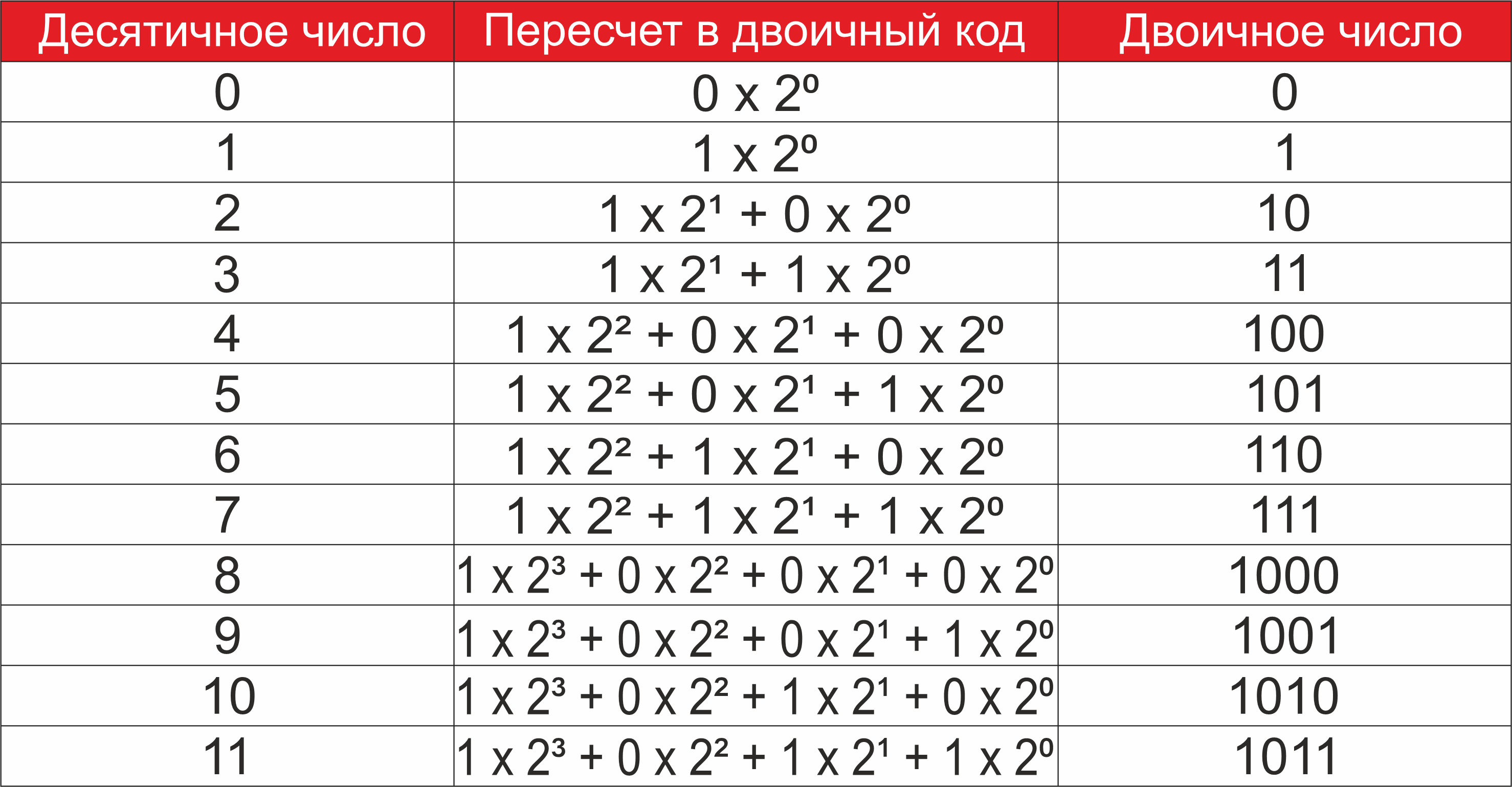
Чтобы перевести обратно, нужно использовать деление с остатком. Исходное число в десятичной системе делим на два, остаток от деления (1 или 0) записываем в первый разряд (самая правая цифра). Полученное частное снова делим на два и остаток записываем уже в следующий разряд. Так действуем, пока в результате деления не получится ноль. Пример ты можешь увидеть на картинке снизу.
Сложение
За операцию сложения в электронных чипах отвечает сумматор. Как складывать двоичные числа? Можно сложить в столбик точно так же, как десятичные. Поскольку цифр всего две, держать в уме и переносить здесь можно только единицу.
Всего возможных вариантов сложения цифр одного разряда четыре:
0 + 0 = 00 + 1 = 11 + 0 = 11 + 1 = 10
В последнем случае единица переходит в следующий разряд, результат записывается как «0 с переносом 1». Этот бит перенесенной единицы складывается с битом в следующем разряде.
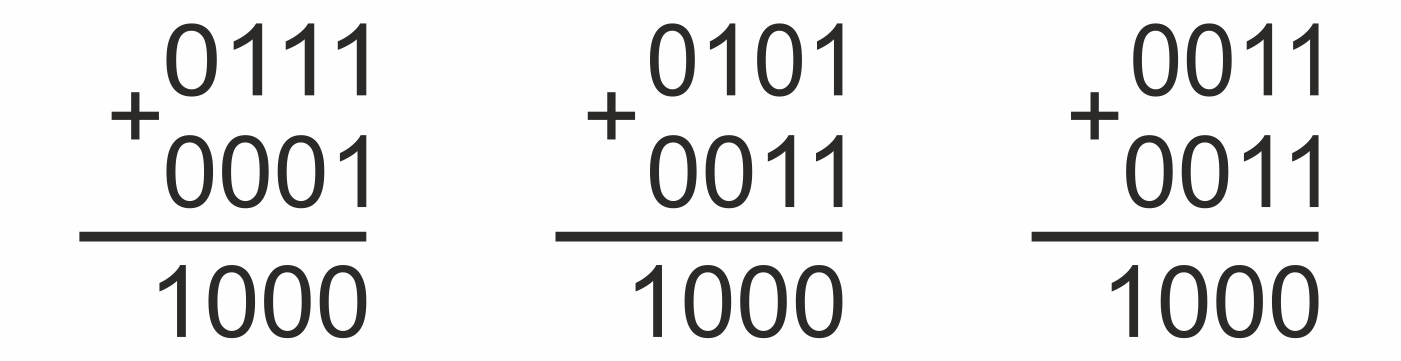
Теперь рассмотрим более сложный пример со складыванием четырехбитных двоичных чисел. В этих случаях все единицы младшего значащего разряда дают в сумме бит нуля с переносом единицы в следующие разряды. Напоминаю, разряды считаются от меньшего к большему (справа налево). В следующем разряде мы снова получаем две единицы от переноса и единицы в разряде. Процесс повторяется до самого старшего значащего бита.
Аналогично и с другими числами в среднем примере. В последнем примере вышедший из младшего разряда бит переноса дает единицу и в сумму, и в бит переноса. Как видишь, это работает точно так же, как с десятичными числами, а может, даже и проще.
Вычитание
Если при сложении нам нужно переносить числа, то при вычитании потребуется занимать. Работает это точно так же, как при десятичном вычитании в столбик.
Есть и другой метод вычитания — сложением двух чисел, при котором мы представим вычитаемое в виде отрицательного числа. Так, из 5 – 2 = 3 получим 5 + (–2) = 3.
Чтобы преобразовать двоичное число в отрицательное, используется дополнительный код. Принцип в следующем. К каждому двоичному числу (и положительному, и отрицательному) добавляется слева еще один бит. Если бит равен нулю, то все остальные биты обозначают положительное число, если равен единице, то отрицательное. Этот бит называется битом знака числа.
Таким образом, положительное число остается таким же, как и было, но с дополнительным нулем в начале, а отрицательное — с единицей слева, с инвертированными цифрами, соответствующими положительному числу, и с добавленной к младшему разряду единицей. То есть если десятичному числу 13 соответствует отрицательное –13, то двоичному значению тринадцати, записанного восемью разрядами, 0,0001101 (первый ноль — это и есть бит знака числа) соответствует отрицательное 1,1110010 + 1 = 1,1110011. Здесь единица слева — это знаковый бит, остальные цифры инвертированы, а к самому правому, младшему, разряду прибавлена единица.
Соответственно, для вычитания такие числа складываются.

Умножение
Умножение тоже выполняется по правилам десятичных чисел. Двоичные числа можно записать в столбик, а потом поразрядно перемножить второе на первое.

Можно заметить некоторые особенности. При умножении на единицу в любом из разрядов второго множителя записывается сам первый множитель со сдвигом на соответствующее количество битов. А при умножении на ноль в строку записываются все нули. Далее все промежуточные произведения складываются с соблюдением разрядности.
АРИФМЕТИКО-ЛОГИЧЕСКИЕ УСТРОЙСТВА
АЛУ — это блок процессора, выполняющий арифметические и логические операции с данными. В прошлой статье я подробно разбирал базовые блоки алгебры логики — если ты успел все забыть, рекомендую освежить знания.
Говоря про операции, мы начали со сложения, поэтому изучать АЛУ будем тоже с самого базового блока — сумматора.
Сумматор
Снова взглянем на комбинации при сложении.
0 + 0 = 00 + 1 = 11 + 0 = 11 + 1 = 10
Результат сложения двух однобитных чисел будет занимать максимум два бита — бит суммы и бит переноса.
Бит суммы для однобитных чисел можно сформировать с помощью вентиля логического исключающего ИЛИ, а бит переноса — с помощью И.
Теперь мы можем составить таблицу истинности для полусумматора, то есть буквально половины сумматора. Выход исключающего ИЛИ обозначается греческой буквой сигмой, Σ (если ты вспомнишь математику, там она обозначает сумму), а бит переноса — CO (Carry Output, выход переноса).

Почему только половина сумматора? Смысл в том, что такое устройство может складывать только однобитные числа, потому что у него нет входа для бита переноса из предыдущих разрядов. Редко когда требуется складывать числа, состоящие из одного бита, поэтому нам необходим полный сумматор.
Полному сумматору понадобится тот самый вход для бита переноса из предыдущих разрядов, он будет брать и прибавлять к нужному разряду число, «хранящееся в уме».
Совместив два полусумматора, мы получим полный сумматор. В его таблице истинности первые четыре строки точно такие же, как у полусумматора, а вот оставшиеся четыре заполняются так: ненулевой бит переноса суммируется с битами слагаемых. Интересна последняя строка, в ней складываются три единицы, что дает единицу и в сумме, и в переносе.

Если для сборки полного сумматора использовать два полусумматора, то нам понадобится еще вентиль логического ИЛИ, и выглядеть схема будет так.

Зная алгебру логики, мы можем упростить схему так, чтобы в ней использовалось всего два типа вентилей — И — НЕ и исключающее ИЛИ.

С помощью однобитного сумматора можно создавать сумматоры на любое количество битов, просто комбинируя их. Сумматоров надо взять столько, сколько разрядов в складываемых числах. На рисунке показан способ соединения сумматоров для четырехразрядного сумматора. Такое устройство называется параллельным сумматором, ведь все биты слагаемых на входы подаются одновременно, буквально параллельно.

На рисунке есть шины — многобитные сигналы. Они обозначаются при помощи квадратных скобок, в которых через двоеточие записаны старший и младший бит, например A[3:0], B[3:0].
INFO
В англоязычной литературе шина называется bus, что логично, ведь много одинаковых проводников собраны вместе, как пассажиры в автобусе. А вот название «шина», скорее всего, произошло от немецкого слова schiene (рельс).
На входы показанного на схеме сумматора подаются два слагаемых по четырехразрядным шинам A[3:0] и B[3:0]. Выходная шина суммы здесь обозначена Σ[3:0]. Внутри схемы каждый из сигналов побитно приходит на отведенный ему полный сумматор, который объединен со следующим полусумматором через сигнал переноса. Такую схему при необходимости легко дорастить до требуемой разрядности.
Параллельный сумматор — устройство простое, и его быстродействие невысоко. Бит переноса всего сумматора СО создается при последовательном прохождении сигналов от младшего значащего разряда к старшему. Таким образом, задержка будет определяться длиной всей этой цепочки. Поэтому параллельную схему применяют нечасто. Но для наших целей это более удобный вариант, чем продвинутые и быстрые, но сложные алгоритмы.
Универсальный сумматор-вычитатель
Аналогично сумматору можно создать двоичный вычитатель. Отличие в том, что вместо бита переноса в старший разряд в вычитателе есть бит займа. Все так же, как при вычитании в столбик на математике: ставим точку над более старшим разрядом, чтобы занять единицу, если в предыдущем разряде вычитаемое было больше уменьшаемого.
Чтобы не городить отдельный вычитатель, мы можем воспользоваться вычитанием через прибавление отрицательного числа. Думаю, ты помнишь, как делаются отрицательные двоичные числа: добавляем слева один бит, если он равен нулю, то все последующие биты кодируют положительное число, а если единице, то отрицательные. Биты отрицательных чисел инвертируются.
Например, +1 будет записано как 001, а –1 находится как его инверсия плюс единица: 110 + 1 = 111. Из положительной двойки +2 = 010 получится –2 точно таким же образом: 101 + 1 = 110
Теперь разберем непосредственно вычитание с помощью дополнительного кода. Возьмем пример 8 – 5. Восьмерка, четырехбитное число с пятым знаковым, будет 01000, а –5 в таком же формате — 11010 + 1 = 11011. Складываем эти два числа и получаем:
01000 + 11011 = 00011
Результатом будет +3, как и должно быть. Теперь попробуем из 5 вычесть 8:
00101 + 11000 = 11101
Результат — это дополнительный код числа –3, так что все правильно.

На рисунке сверху изображена схема универсального сумматора‑вычитателя, использующего дополнительный код. Вход MODE в ней служит переключателем режимов. Если его значение равно логическому нулю, то вся схема работает как сумматор.
Сигналы на выходах B[0] и B[1] дополнительных элементов исключающее ИЛИ (на схеме они слева от полных сумматоров) будут, соответственно, совпадать с сигналами на входах С[0] и C[1].
То же самое будет и с выходом СО полного сумматора (снизу на схеме), проходящего через свое исключающее ИЛИ. Таким образом, выход S в этом режиме продолжит работать как бит переноса.
Если же на MODE подать логическую единицу, то добавленные вентили исключающее ИЛИ инвертируют шины C[1:0] и к результату инверсии будет прибавлена единица, попадающая со входа MODE на вход CI первого полного сумматора. Это значит, что теперь шина A[1:0] задает уменьшаемое, а шина C[1:0] — вычитаемое, которое внутри схемы преобразуется в отрицательное число для сложения с уменьшаемым на этом же сумматоре. А выход CO нижнего сумматора будет играть роль знакового бита в дополнительном коде. В итоге все очень удобно: один и тот же сигнал используется и для переключения режимов работы, и для преобразования числа в дополнительный код.
Умножители
Переходим к умножению. Как умножать в двоичной системе, мы уже разобрались, осталось понять, как сделать умножитель из сумматора. Для этого нужно один из множителей побитно сдвигать влево и, если соответствующий бит второго множителя равен единице, прибавлять сдвинутый первый множитель к частичной сумме. Если же бит равен нулю, то прибавление пропускается. Это не единственная схема умножения, но такое сложение со сдвигом довольно эффективно.
Однако умножитель я здесь привел просто как пример АЛУ, собирать мы его сегодня не будем. Перед этим еще понадобится разобрать схемы временного хранения промежуточных результатов для частичных сумм и реализацию побитового сдвига, а это тема для отдельной статьи.
Переходим к АЛУ
Итак, на базе сумматора с разными дополнительными блоками в микросхемах создается арифметико‑логическое устройство, то есть вычислительное ядро процессора.

На этой схеме есть несколько входов, задающих выполняемую операцию, такую как сложение, умножение и так далее, а также операнды, над которыми эта операция выполняется. Также у АЛУ есть флаги — поступающие и выходящие из него служебные сигналы, которые дополняют или уточняют то или иное выполняемое действие.
Разрядность операндов обозначена на схеме красной чертой, которая пересекает обозначение входа. Рядом с чертой записывается количество разрядов.
СОБИРАЕМ АЛУ
От слов к делу. Берем в руки макетную плату, микросхемы, проводки, хорошее настроение — и вперед!
Однобитный полный сумматор
Начнем с самого простого — однобитного полного сумматора. Еще раз взгляни на его схему. Используя знания о микросхемах, превратим ее в принципиальную схему устройства, по которой уже можно собирать сумматор.
На макетной плате схема будет выглядеть так.

Нам потребуется всего две микросхемы: CD4070BE и CD4011BE. На схеме есть два светодиода. Верхний светодиод показывает значение бита суммы, а нижний — бита переноса. Горящий светодиод равен единице, не горящий — нулю.
Двухбитный сумматор
Теперь давай на основе прошлой схемы соберем двухбитный сумматор. В нашем исполнении один разряд будет полностью повторять второй. Первые два ползунка переключателя используются, чтобы задавать значение слагаемого A[1:0], а два последних — слагаемого B[1:0].
Наиболее корректно располагать биты в переключателях, сумматорах и индикаторах так же, как и в числах: чтобы младший разряд был слева, а старший — справа. На схеме синими проводами показаны подключения внутри полных сумматоров, а зелеными — индикаторные связи. Коричневый провод соединяет выходной бит переноса нулевого разряда с входным переносом первого. CI берется не с переключателя, а прямо с нужной шины питания.

Универсальный сумматор-вычитатель
Давай теперь переработаем предыдущую схему в сумматор‑вычитатель, основываясь непосредственно на его логической схеме. Используем оставшиеся в микросхеме CD4070BE вентили исключающего ИЛИ и немного поменяем расположение проводов.

Здесь нижний светодиод в режиме вычитания показывает знак числа, получившегося в результате вычисления.
ВЫВОДЫ
Сегодня мы наконец разобрали основу всей цифровой электроники — арифметико‑логические устройства. Дорабатывая сумматор, мы сможем получить новые АЛУ.
Читайте ещё больше платных статей бесплатно: https://t.me/hacker_frei