Греко-латинские квадраты Эйлера

Даже Эйлер, один из самых гениальных математиков всех времён и народов, смог ошибиться на своём профессиональном поприще! Нет, он не совершил математической ошибки, но сформулировал гипотезу, которая была опровергнута спустя почти два века. Опровержение гипотезы великого учёного, имеющего столь великолепную математическую интуицию, само по себе является значительным математическим событием.
Эйлер занимался латинскими квадратами. Это такие таблицы размером n×n, заполненные n различными символами, каждый из которых в каждой строке и в каждом столбце таблицы встречается ровно один раз. Само название «латинские квадраты» вдохновлено работами Эйлера, который для их заполнения использовал буквы латинского алфавита.
Сегодня латинские квадраты находят широкое применение в алгебре, комбинаторике, статистике, криптографии, теории кодов и многих других областях.
Существует ряд игр, в которых используются латинские квадраты. Наиболее известна из них судоку. В ней требуется частичный квадрат дополнить до латинского квадрата 9-го порядка, обладающего дополнительным свойством: все девять его подквадратов содержат по одному разу все натуральные числа от 1 до 9.

Внимание Эйлера к латинским квадратам было вызвано изучением более сложных математических объектов — греко-латинских квадратов. Для объяснения этого понятия рассмотрим на примере два различных латинских квадрата 4×4:
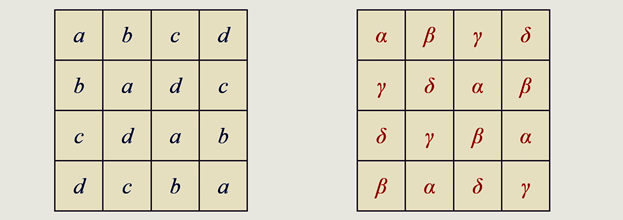
Если теперь совместить эти два латинских квадрата, то мы получим новый квадрат, такой что каждая латинская буква соединится с каждой греческой буквой один единственный раз:

Образованный таким образом квадрат называют греко-латинским, или квадратом Эйлера. А сами два латинских квадрата, обладающие свойством образовывать при соединении греко-латинский квадрат (т.е. не имеющий одинаковых пар), называют взаимно-ортогональными.
Приведённый греко-латинский квадрат представляет собой одно из решений старинной головоломки: расположить в сетку 4×4 выбранных из стандартной колоды карт всех валетов, дам, королей и тузов так, чтобы каждый ряд и каждая колонка содержали все 4 наименования и все 4 масти. Данное решение обладает дополнительным свойством — цветовые варианты расположены в шахматном порядке:

Имеется другое решение, удовлетворяющее иному дополнительному условию — две главные диагонали содержат все четыре масти и все четыре наименования:

Интересно, что сам Эйлер не придавал практического значения изучению греко-латинских квадратов. Однако в ХХ в. они нашли применение при планировании экспериментов в сельском хозяйстве, биологии, медицине, социологии, маркетинге и т. д.
Например, пусть имеется система, на которую действуют 4 различных параметра (скажем, воздействие n различных медикаментов на пациентов n различных возрастных групп, n различных весовых категорий и n различных стадий одной и той же болезни). Наиболее эффективной конструкцией, которую может использовать исследователь в данном случае, является греко-латинский квадрат n-го порядка, отобранный случайным образом из всех возможных квадратов этого порядка. (При необходимости исследования влияния большего количества переменных можно использовать наложение дополнительных латинских квадратов, хотя для любого порядка n существует не больше n – 1 взаимно ортогональных квадратов.) Тогда параметры будут соответствовать ряду, столбцу, первому и второму числу (это и есть 4 параметра). Таким образом, можно провести n² экспериментов, вместо n⁴ (в случае полного перебора вариантов, если бы учёные не знали про греко-латинские квадраты). Греко-латинский квадрат является просто моделью эксперимента. Его ряды представляют одну из переменных, колонки — другую, латинские буквы — третью, а греческие буквы — четвёртую.
Теперь самый главный вопрос: для каких значений n существуют греко-латинские квадраты?
Легко убедиться, что для n = 2 греко-латинского квадрата не существует. Для 3-го, 4-го, 5-го порядка они были известны во времена Эйлера. А что можно сказать о квадратах 6-го порядка?
Эйлер сформулировал (1779 г.) этот вопрос в виде задачи о 36 офицерах (а согласно неподтверждённой легенде, ему предложила решить эту задачу императрица Екатерина Великая):
Необходимо разместить 36 офицеров шести различных полков (скажем, уланов, драгунов, гусаров, кирасиров, кавалергардов и гренадёров) и шести различных воинских званий (полковников, подполковников, майоров, капитанов, поручиков и подпоручиков) в каре так, чтобы в каждой колонне и в каждом ряду был ровно один офицер каждого полка и каждого воинского звания.
Эта задача эквивалентна построению двух ортогональных латинских квадратов 6-го порядка. Эйлер предположил, но не смог доказать, что такие квадраты построить невозможно. Лишь спустя 122 года, в 1901 г., француз Гастон Терри, проанализировав все 9408 таких квадратов, показал, что при любом их сочетании невозможно построить пару ортогональных квадратов. И таким образом дал отрицательное решение задачи о 36 офицерах.
В своём мемуаре о греко-латинских квадратах Эйлер написал: «Я не сомневаюсь в том, что невозможно построить квадраты 6-го, 10-го, 14-го порядка и вообще, если порядок равен любому нечётно-чётному числу» (то есть числу вида n = 4k + 2). Эта гипотеза Эйлера в течение 180 лет считалась неопровержимой.
Но в 1959 г. она была опровергнута американцами Э.Т. Паркером, Р.К. Боусом и С.С. Шрикхендом, которым (конечно же с помощью компьютера) удалось построить греко-латинский квадрат 10 порядка. Вот он:

(символы одного латинского квадрата — первая цифра, а второго — вторая).
На рисунке вначале заметки приведена обложка журнала Scientific American за ноябрь 1959 года. На ней изображён греко-латинский квадрат 10-го порядка, в котором 10 цифр заменены 10 различными красками.
Позже также было установлено, что гипотеза Эйлера ошибочна для всех значений n > 6. Таким образом, существуют греко-латинские квадраты любого порядка, кроме 2-го и 6-го.
Новая эра головоломки Эйлера о 36 офицерах началась в 2021 г. Неожиданно она получила положительное «решение» с помощью странной физики кота Шрёдингера. В журнале Physical Review Letters группа квантовых физиков из Индии и Польши продемонстрировала, что можно расположить 36 офицеров таким образом, чтобы они соответствовали критериям головоломки Эйлера, но при условии, что офицеры могут иметь квантовую смесь званий и полков.
В явлении квантовой запутанности используется тот факт, что квантовые объекты, пока они не измерены, могут находиться в нескольких возможных состояниях. В классическом понимании один конкретный офицер может иметь только одно конкретное звание и принадлежать только к одному конкретному полку. А если задачу пытаться решить с помощью квантовой запутанности, то один и тот же офицер может принадлежать более чем одному полку и иметь разные звания одновременно до какого-либо момента. При этом состояние одного объекта информирует о состоянии другого: то есть, если первый офицер на самом деле является полковником кирасиров, то второй должен быть поручиком гусаров, и наоборот.
По мнению открывших это явление учёных, полученные результаты могут оказать реальное влияние на хранение квантовых данных. Запутанные состояния могут использоваться в квантовых вычислениях для обеспечения безопасности данных даже в случае ошибки — процесс, называемый квантовой коррекцией ошибок.
Вот мог ли Эйлер в XVIII в. помыслить о появлении квантовых офицеров, когда формулировал свою головоломку?