Global BP

Новая сеть. Назвал её условно Global BP.

* после того как сделал, понял, что она похожа на FFA, но я пришёл к идеи с другой стороны

Это бинарный классификатор на многослойной сети. Фишка в том, что ожидаемое значение (Y) дирижирует напрямую всеми нейронами в сети, а не одним единственным выходным нейроном.

Обучение

Делается прямой проход по сети (FF). При этом нормализация выхода слоя ускоряет обучение.

Далее каждый нейрон сети обновляет свои веса. Формула классическая (из BP):

𝐖 += 𝐗·delta;

, где delta считается от ошибки err и производной от функции активации.

Ошибка одинаковая для всех нейронов одного слоя.

e = 𝐘·0.5 - mean(Outs);
err = sign(e)·e^2;

, mean(Outs) – среднее значение выхода слоя, 𝐘 – ожидаемое на выходе сети бинарное значение.

Собственно и всё.

Сеть можно разбить на две условные: экстрактор фич и выходной слой из единственного нейрона.

Выходной нейрон видит только последний скрытый слой (последний слой экстрактора) и обучает веса по своей ошибке. Экстрактор же перестраивает свою структуру так, чтобы активность всех его нейронов была минимальной, когда Y равно нулю и максимальной, когда Y равно единице.

Обратной связи от выходного нейрона к нейронам экстрактора нет. Можно сказать они обучаются независимо, вначале можно обучить экстрактор, потом – выходной нейрон. В эксперименте я задействовал в обучении выходного нейрона только последний слой экстрактора, но намного лучше будет подключить этот нейрон ко всем нейронам экстрактора, что ускорит обучение.

Картинки

Конфигурация сети [3, 8, 8, 8, 1]. Обучалась XORу.

[x1, x2, x3] = y. y = x1^x2

0, 0, 0 = 0
0, 0, 1 = 0
0, 1, 0 = 1
0, 1, 1 = 1
1, 0, 0 = 1
1, 0, 1 = 1
1, 1, 0 = 0
1, 1, 1 = 0

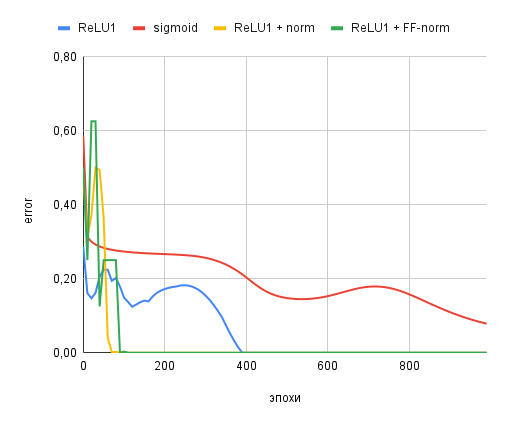
Тест с функциями активации сигмоида и ReLU1 и нормализацией. Наибыстрейшее обучение показал вариант ReLU1 с нормализацией во время FF-прохода.

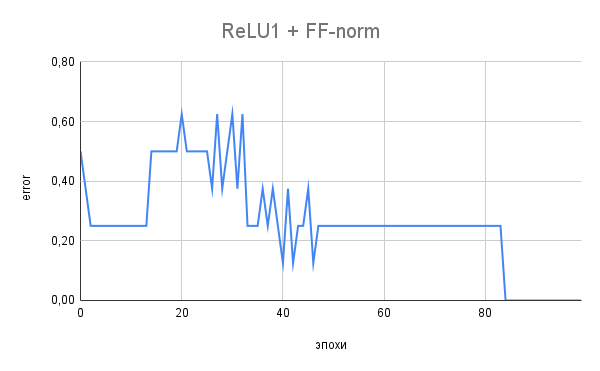
На следующем графике показан лучший вариант. Обратите внимание на "цифровой" характер смены ошибки. Она принимает "квантованные" значения:

0.625, 0.500, 0.375, 0.250, 0.125, 0.000