Функции потерь для классификации

Автор: Александр Лекомцев

Функция потерь — это численное выражение ошибки модели. Поскольку современные нейросети обучаются методом обратного распространения, эта функция должна быть дифференцируема. Из-за требования к дифференцируемости нам не подходят accuracy, precision и подобные метрики. В этом посте мы вспомним, какие есть распространенные функции потерь для задачи классификации.

Brier Score (MSE)

Если мы решаем задачу бинарной классификации, то на выходе из модели получаем единственное число — вероятность принадлежности к классу 1. Тогда почему бы не использовать знакомую по задаче регрессии mean squared error, сравнивая вероятность с меткой класса?

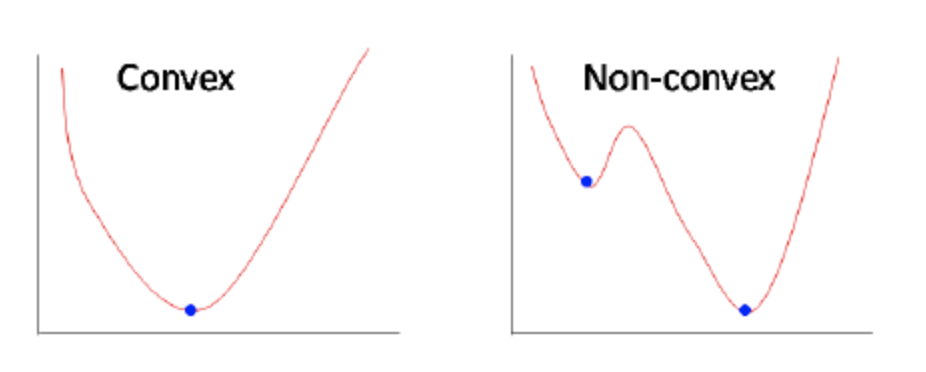
Мы знаем, что MSE (называемая Brier Score в задаче классификации) хорошо показывает себя при нормальном распределении таргета, но в задаче бинарной классификации таргет имеет распределение Бернулли. Кроме того, MSE не является выпуклой функцией при бинарной классификации, подробнее почему это так можно прочитать по ссылке. Но следствие из этого следующее: выпуклая функция потерь всегда имеет глобальный минимум, и все дороги ведут к нему, а вот в случае невыпуклой можно застрять в локальном минимуме.

Главное отличие классификации от регрессии — в классификации нельзя задать порядок на множестве классов. Нельзя сказать что “кошка больше собаки”. Но если в задаче присутствуют порядковые отношения, или вы решаете задачу регрессии, то MSE отлично подходит. Например, партия металла с концентрацией примесей выше порога является бракованной — можно рассматривать эту задачу и как классификацию (концентрация выше/ниже порога), и как регрессию (предсказание концентрации).

Если же в вашей задаче у классов все таки наблюдается какой-то порядок, то можно использовать weighted kappa loss. Он позволяет меньше штрафовать за ошибку между близкими классами.

Кстати, Brier Score можно использовать и при мультиклассовой классификации, тогда проявляется ещё одна интересная особенность — штраф за ответы (.8, .1, .1) (.8, .2, .0) при истинных метках (1, 0, 0) будет больше для второго, а для остальных лоссов в этой статье результат будет одинаковый.

Тут и далее в формулах N - количество элементов в выборке, pt - уверенность модели, yt - метка класса.

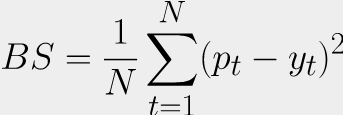
Binary Cross-Entropy

Можно вспомнить, как вообще появилась MSE в статистике. При обучении классической линейной регрессии оптимизация MSE эквивалентна нахождению ответа методом максимального правдоподобия. Что если мы пойдем тем же путем для задачи классификации на два класса? Мы получим бинарную кросс-энтропию! В этом плане MSE и BCE — продукты одного и того же метода, примененного к разным задачам. С помощью бинарной кросс-энтропии (она же logloss) можно решать и мультилейбл классификацию — достаточно для каждого класса завести отдельную голову, решающую относится ли объект к этому классу. Тогда итоговый лосс будет суммой бинарных кросс-энтропий для каждого класса. Короче говоря, очень универсальная штука с математическим обоснованием, не удивительно, что её используют чаще остальных функций.

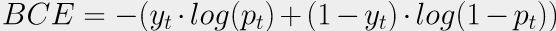
Cross-Entropy

Но что если стоит задача мультиклассовой классификации — классов больше, чем два, при этом они взаимоисключающие? Научиться классифицировать каждый класс отдельно и выбирать по максимальному скору не получится, из-за того, что уверенность в нейронных сетях не калибруется сама по себе. Находить argmax среди скоров и штрафовать за неверный индекс тоже не выйдет, так как максимум не дифференцируем. Но ничего не мешает нам обобщить бинарную кросс-энтропию до категориальной, называемой также просто кросс-энтропией. Для этого поменяем финальные функции активации. Несколько сигмоид (по одной для каждой головы) заменим на softmax. Уверенность всё ещё будет в диапазоне (0, 1), но сумма всех выходов даст единицу. И теперь мы можем считать лосс только для положительного класса, ведь остальные выходы участвуют в софтмаксе и через них градиент потечет в том числе. А уже после обучения, при инференсе, мы сможем просто выбирать максимум по всем скорам.

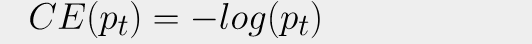
По сути, BCE тоже считается только для “позитивного” класса. Если таргет yt = 1, то позитивным считается “класс единица” и его вероятность равна pt. Если таргет yt = 0, то позитивным считается “класс ноль”, а его вероятность равна 1 - pt. Поэтому CE и BCE часто путают между собой :)

Weighted CE/BCE

Модели, обученные с CE/BCE при дисбалансе классов в обучающей выборке, могут начать выдавать метки только мажорного класса, либо очень редко предсказывать минорный. Но что делать, если нам одинаково важно учитывать все классы?

На помощь приходит взвешивание лосса.

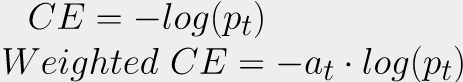
Focal Loss

Но и в Weighted CE/BCE осталась проблема.

В минорном классе могут быть простые объекты, которые сеть выучит легко и быстро. А в мажорном могут встречаться сложные паттерны, выучить которые гораздо труднее. Если дать минорному классу большой вес, то штраф за мелкие ошибки на легких примерах будет переоценен. Обратная ситуация возникнет на сложных примерах мажорного класса, когда из-за маленького веса мы будем прощать сильные ошибки на сложных сэмплах.

Интуиция подсказывает, что надо действовать следующим образом:

• если сеть выдает низкую вероятность верного класса, то надо штрафовать ее сильнее;
• если сеть выдает высокую вероятность верного класса, то можно не обращать на это внимание.

Focal Loss крут тем, что он решает проблему добавлением всего одного множителя! И теперь веса подбираются динамически для каждого объекта, исходя из уверенности в предсказании верного класса. Если из-за дисбаланса мы изначально плохо справляемся с объектами минорного класса, FL будет давать им больший лосс, но когда сеть начнет хорошо с ними справляться, то вес не будет “завышен”. Гиперпараметр гамма отвечает за то, какую уверенность считать достаточной, но зачастую можно оставить дефолтное значение gamma = 2.