♾ От миллиона до числа Грэма
WBWRUSОт миллиона до числа Грэма. Часть 4
Операция уровня 4 — Тетрация (↑↑)
Тетрация — это повторное возведение в степень. Прежде чем мы сможем понять, как получить цепочку возведений в степень так же, как возведение в степень составляет цепочку умножений, нам нужно понять, что вообще такое «цепочка возведений в степень».
Пока всё, что мы делали с возведением в степень, — это одно вычисление — брали основание и возводили его в степень. Но что, если мы соединим два таких вычисления вместе, например:
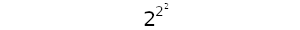
Мы получим степенную башню. Степенные башни невероятно мощны, потому что они начинаются сверху и набирают силу к низу. Так,
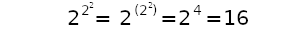
Пока ничего особенного, но зацените вот это:
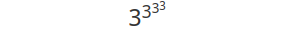
Воспользуемся скобками, чтобы акцентировать внимание на порядок операций сверху вниз:
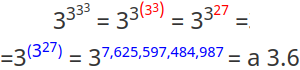
Помните, что гугол и его микроскопические мини-песчинки, заполняющие Вселенную, — это всего лишь 100-значное число? А теперь всё, что требуется, — это степенная башня из троек, уложенных 4 слоями друг над другом, чтобы затмить гугол, а также 10¹⁸⁵ — количество планковских объёмов, чтобы заполнить Вселенную и максимум нашего физического мира. Оно не такое большое, как гуголплекс, но мы можем легко разобраться с этим, просто добавив ещё одну тройку в стек:
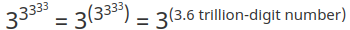
что намного больше, чем гуголплекс, который

Что касается самого гуголплекса, то степенные башни позволяют сразу же унизить его, записав следующим образом:
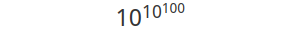
или ещё более наглядно:
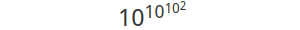
Теперь вы можете представить, какого рода числа вы получите, когда начнёте делать высокие степенные башни. Тетрация сильна.
Сейчас эти башни — это уровень 3, цепочки экспонент, точно так же, как 3 x 3 x 3 x 3 — это цепочка умножений уровня 2. Мы используем уровень 3, чтобы объединить эту цепочку второго уровня в 3⁴, или 3 ↑ 4. Итак, как мы можем использовать уровень 4 для объединения экспоненциальной цепочки? Двойные стрелки.
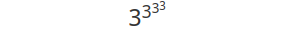
— это то же самое, что 3 ↑ (3 ↑ (3 ↑ 3)). Мы объединяем эти 4 однострелочных тройки в 3 ↑↑ 4.
Так же, 3 ↑↑ 5 = 3 ↑ (3 ↑ (3 ↑ (3 ↑ 3))) =
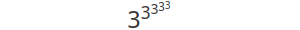
4 ↑↑ 7 = 4 ↑ (4 ↑ (4 ↑ (4 ↑ (4 ↑ (4 ↑ 4))))) = 7-этажная степенная башня четвёрок.
Вот общее правило:
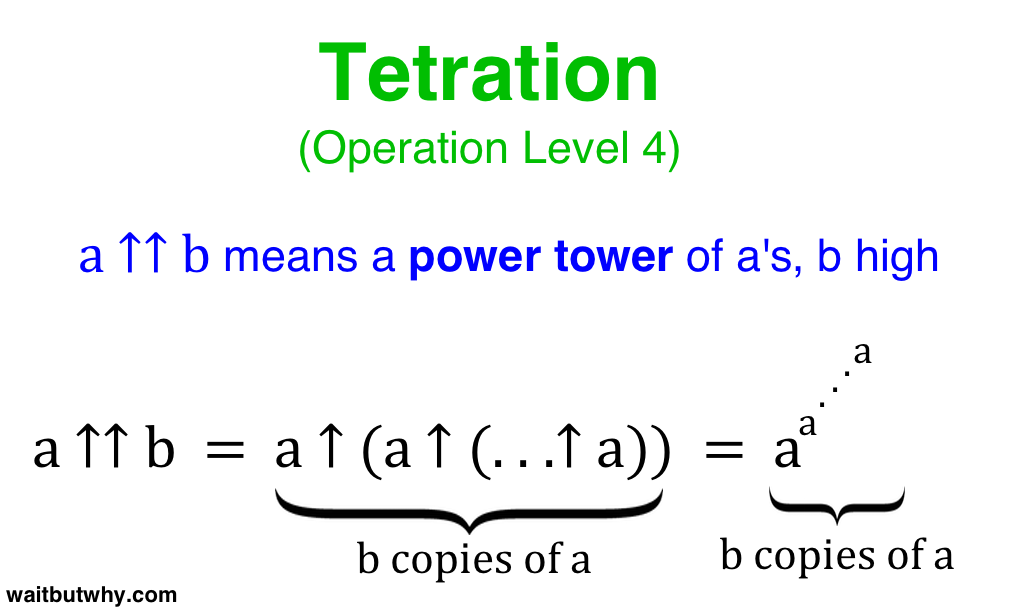
a ↑↑ b означает степенную башню из чисел a высотой b
Мы собираемся подняться на следующий уровень, и сложность повысится, поэтому, прежде чем мы двинемся дальше, убедитесь, что вы действительно разобрались с уровнем 4 и тем, что означает ↑↑ — просто помните, что a ↑↑ b — это степенная башня из а высотой b.
Операция уровня 5 — Пентация (↑↑↑)
Пентация, или повторная тетрация, объединяет цепочки с двойными стрелками в одну операцию.
Шаблон, который мы видели, состоит в том, что каждый новый уровень связывает цепочку предыдущего уровня вместе, используя выражение b в качестве длины цепочки. Например:
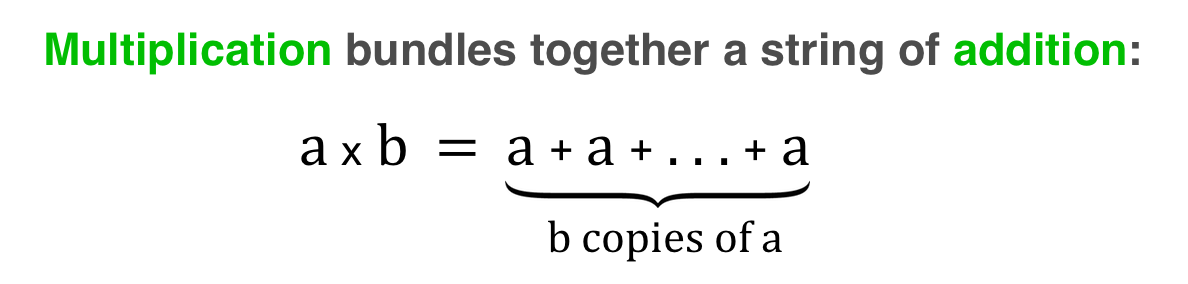
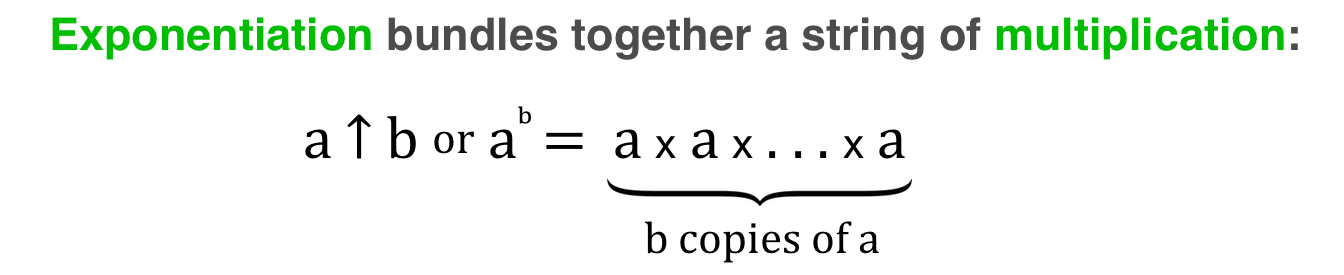
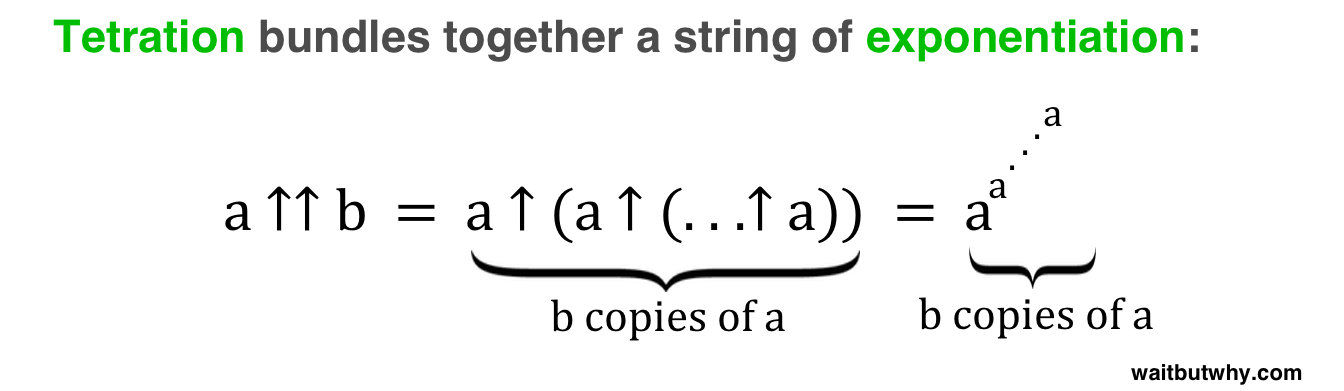
В каждом случае a — это основа, а b — длина объединяемой цепочки.
Так что же объединяет пентация? Как у вас может быть цепочка степенных башен?
Ответ заключается в том, что я называю «безумный пир степенных башен». Вот как это работает.
У вас есть ряд степенных башен, стоящих рядом друг с другом в определённом порядке, и все они используют одну и ту же основу. В чём между ними разница, так это в высоте каждой башни. Высота первой башни равна основе. Вы рассчитываете эту башню до её полного развёрнутого результата, и этот результат становится высотой следующей башни. Затем вы рассчитываете эту башню, и в результате получается высота следующей башни. И так далее. Результат каждой башни «вскармливает» следующую башню и становится её высотой — отсюда и безумный пир. Вот почему это происходит:
3 ↑↑↑ 4 означает последовательность операций (3 ↑↑ 3) длиной 4. То есть:
3 ↑↑↑ 4 = 3 ↑↑ (3 ↑↑ (3 ↑↑ 3))
Как вы помните, когда мы видим ↑↑, это означает, что это одна степенная башня высотой b, поэтому:
3 ↑↑↑ 4 =

Теперь вы, возможно, помните, что:
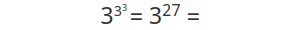
= 7 625 597 484 987. То есть:
3 ↑↑↑ 4 =

= 3 ↑↑ (3 ↑↑ 7 625 597 484 987)
Таким образом, первая башня высотой 3 превратилась в 7-триллионую башню. Следующие скобки, с которыми мы имеем дело, это (3 ↑↑ 7 625 597 484 987), где результат первой башни является высотой этой второй башни. И насколько высокой будет эта башня из 7 триллионов 3?
Что ж, если каждая 3 будет иметь высоту два сантиметра, а написанные мною тройки примерно такой высоты, башня поднимется примерно на 150 миллионов километров в высоту и коснётся солнца. Даже если бы мы использовали крошечные, напечатанные двухмиллиметровые тройки, наша башня достала бы до Луны, вернулась обратно на Землю и снова достала до Луны, и так — сорок раз. Если бы вместо этого мы написали крошечные тройки на поверхности планеты, башня обернулась бы вокруг Земли 400 раз. Назовём эту башню «солнечной башней», потому что она простирается до самого солнца. Итак, что у нас есть:
3 ↑↑↑ 4 =

= 3 ↑↑ (3 ↑↑ 7 625 597 484 987) = 3 ↑↑ (солнечная башня)
Эта последняя операция 3 ↑↑ (солнечная башня) — это степенная башня из 3, высота которой — это число, которое вы получите, если вычислите всю солнечную башню (и эта последняя башня, которую мы строим, даже близко не будет соответствовать наблюдаемой Вселенной). И мы не дойдём до нашего окончательного значения 3 ↑↑↑ 4, пока не вычислим эту последнюю башню.
Таким образом, использование ↑↑↑, или пентации, создаёт безумный пир степенных башен, когда по мере продвижения высота каждой башни начинает становиться непостижимой, не говоря уже о фактическом окончательном значении. Если обобщить:

a ↑↑↑ b означает безумный пир степенных башен из b башен a
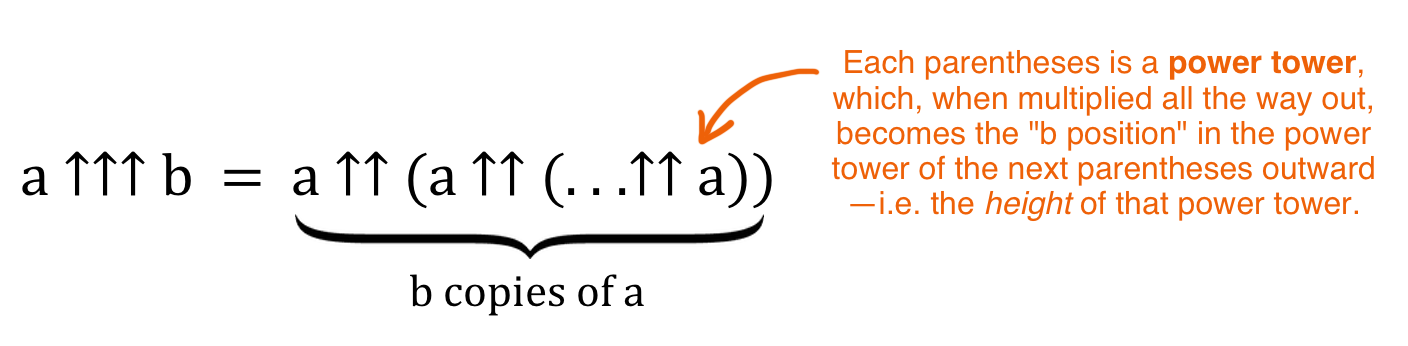
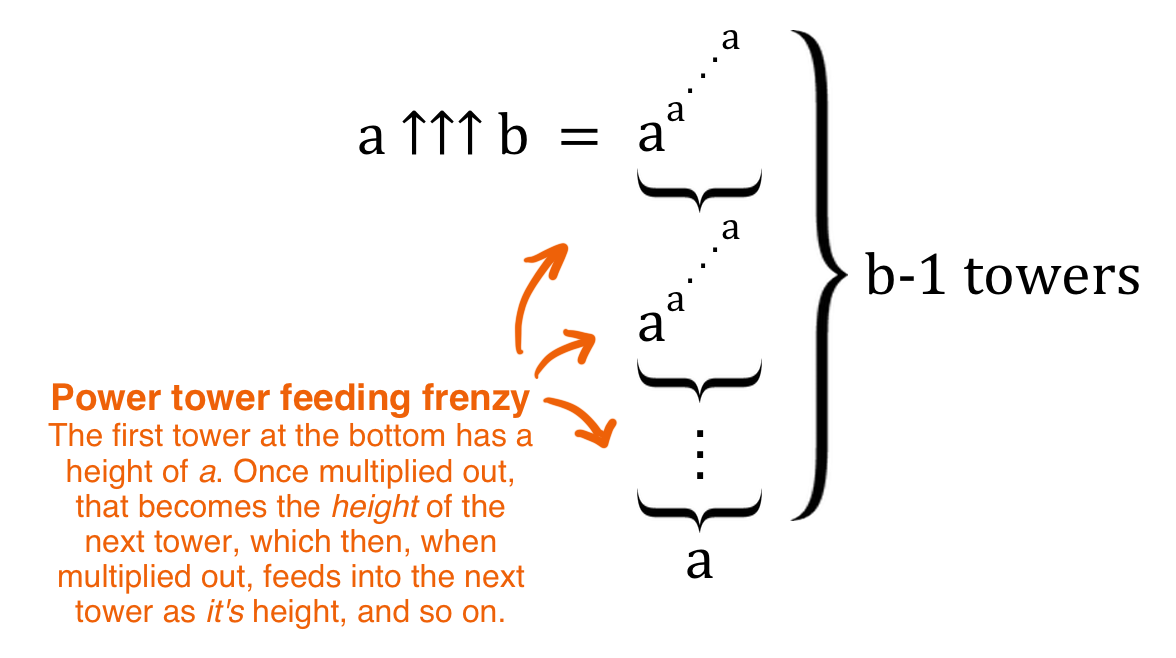
первая башня внизу имеет высоту a. Будучи рассчитанной, она становится высотой следующей башни, которая будучи рассчитанной в свою очередь становится высотой следующей башни и так далее
Мы собираемся подняться ещё на один уровень —
Операция уровня 6 — Гексация (↑↑↑↑)
Итак, на уровне 4 мы имеем дело с цепочкой экспонент третьего уровня — степенной башней. На уровне 5 мы имеем дело с цепочкой степенных башен четвёртого уровня — безумным пиром степенных башен. На уровне 6, также известном как гексация или повторная пентация, мы имеем дело с цепочкой безумных пиров степенных башен — то, что мы назовём «психофестивалем безумных пиров степенных башен». Вот основная идея:
Происходит безумный пир степенных башен. Последнее число, которое получилось в результате этого безумия, становится количеством башен в следующем безумном пире степенных башен. Затем происходит уже это безумие, и оно производит ещё более нелепое число, которое затем становится количеством башен для следующего безумия. И так далее.
3 ↑↑↑↑ 4 — это психофестиваль безумных пиров степенных башен, во время которого происходят все 3 ↑↑↑ безумных пира степенных башен, каждый из которых определяет количество башен в следующем. Так:
3 ↑↑↑↑ 4 = 3 ↑↑↑ (3 ↑↑↑ (3 ↑↑↑ 3))
Теперь вспоминаем, что 3 ↑↑↑ 3 — это то, что превращается в солнечную башню. Так:
3 ↑↑↑↑ 4 = 3 ↑↑↑ (3 ↑↑↑ (3 ↑↑↑ 3)) = 3 ↑↑↑ (3 ↑↑↑ (солнечная башня))
Поскольку ↑↑↑ означает безумный пир степенной башни, то наше 3 ↑↑↑ (солнечная башня), — это безумный пир из башен, число которых равно рассчитанной солнечной башне. Когда этот пир, наконец, заканчивается, результатом становится количество башен в последнем безумном пире. Психофестиваль заканчивается, когда этот последний безумный пир производит окончательный результат. Вот общее объяснение гексации:

a ↑↑↑↑ b означает психофестиваль безумных пиров степенных башен из b башен a
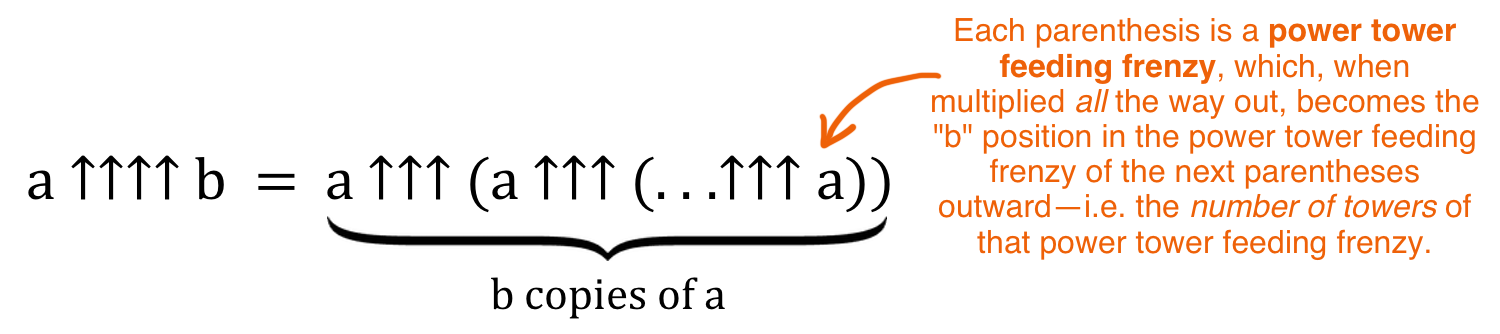
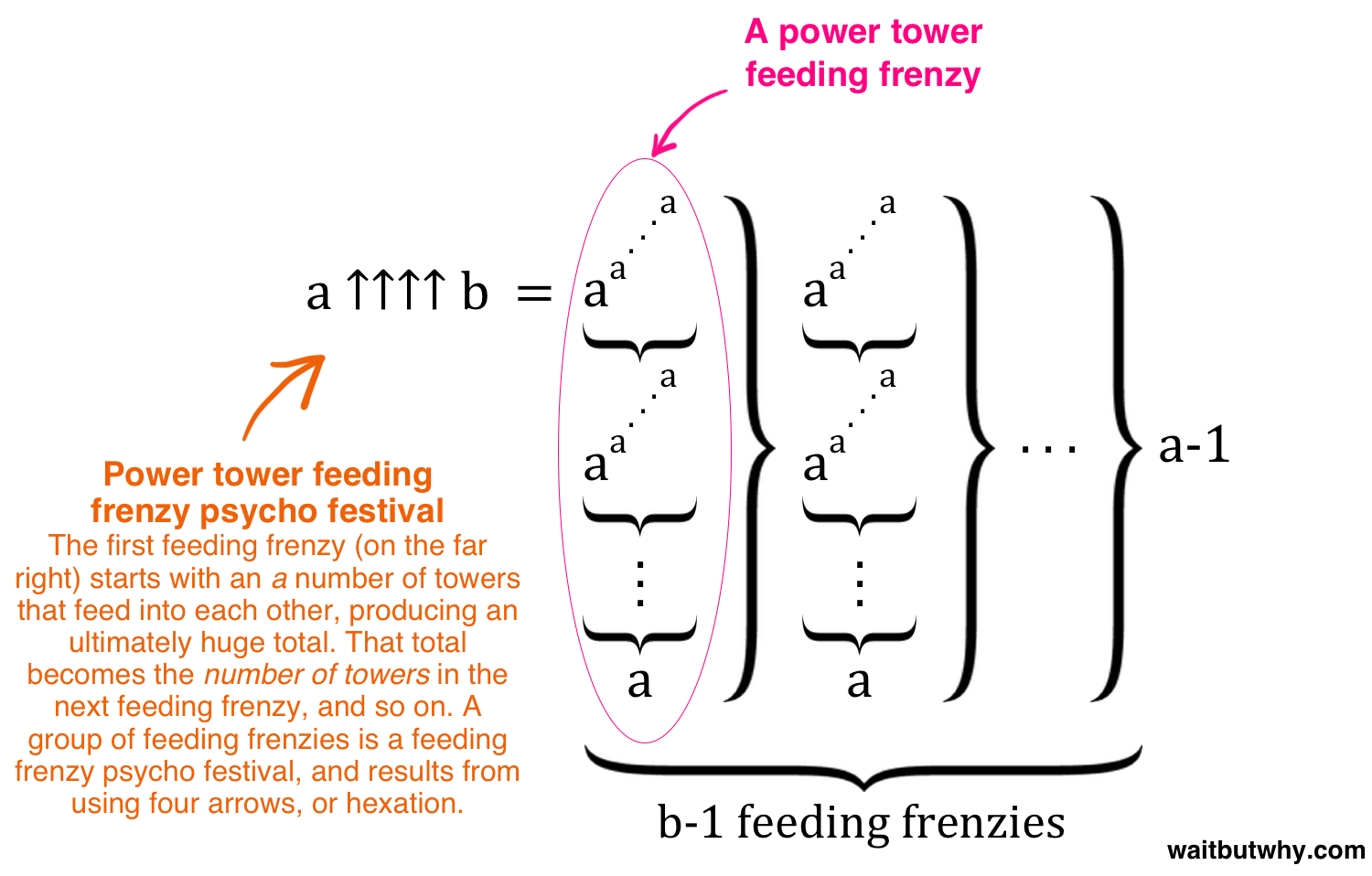
первый безумный пир (с правого края) начинается с a башен, вскармливающих друг друга, производя абсолютно огромное значение. Этот итог становистя числом башен в следующем безумном пире и так далее. Группа безумных пиров — это психофестиваль безумных пиров и результат использования четырёх стрелок, или гексация
Вот как работает последовательность гипероператоров. Вы можете увеличивать количество стрелок, и каждая добавленная вами стрелка радикальным образом расширяет область действия, с которой вы имеете дело. Пока что мы выполнили первые семь операций в последовательности, включая первые четыре уровня стрелок:
↑ = степень
↑↑ = степенная башня
↑↑↑ = безумный пир степенных башен
↑↑↑↑ = психофестиваль безумных пиров степенных башен
Итак, теперь, когда у нас есть инструментарий, давайте перейдём к числу Грэма.