Формулы Блэка – Шоулза

Стоимость любого будущего актива определяется будущим денежным потоком FV (Future Value), который он принесет, дисконтированным на временную стоимость денег e^(-RT). Это общее правило инвестиций позволяет определить стоимость опциона CALL, как:

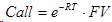
Напомним, что здесь R и T – безрисковая ставка и срок до исполнения опциона в долях года. И если безрисковая ставка и срок обращения опциона нам известен, то осталось найти лишь будущие выплаты по опциону, что позволит точно рассчитать теоретическую стоимость опциона CALL.

Функция выплат опциона CALL нам известна. Она равна внутренней стоимости опциона на экспирацию: S(T)-X. Где S(T) – цена базисного актива в момент экспирации.  Однако сама цена S(T) нам не известна и может в будущем с определенной вероятностью принять практически любое значение. Ниже приведен характерный рисунок, показывающий вероятности распределение цен в диапазоне.

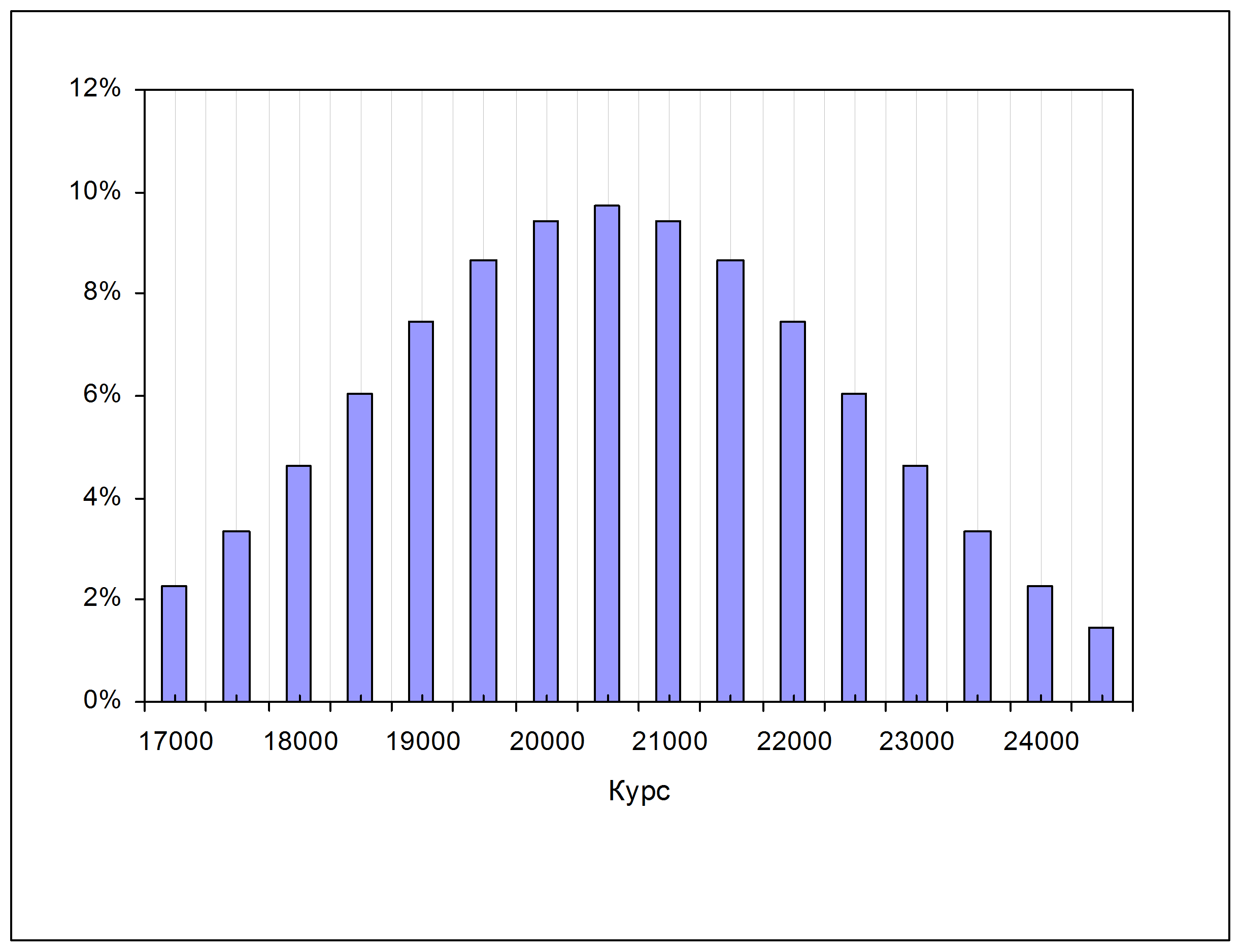
Видно, что вероятность значительного уклонения цены от «центра», определяемого текущим положением рыночной цены, резко уменьшается по мере удаления от этого центра.

Для расчета ожидаемого денежного потока остается перемножить эти вероятности на внутреннюю стоимость опциона для разных величин S(T) и все сложить.

Результат перемножения показан на следующем рисунке:

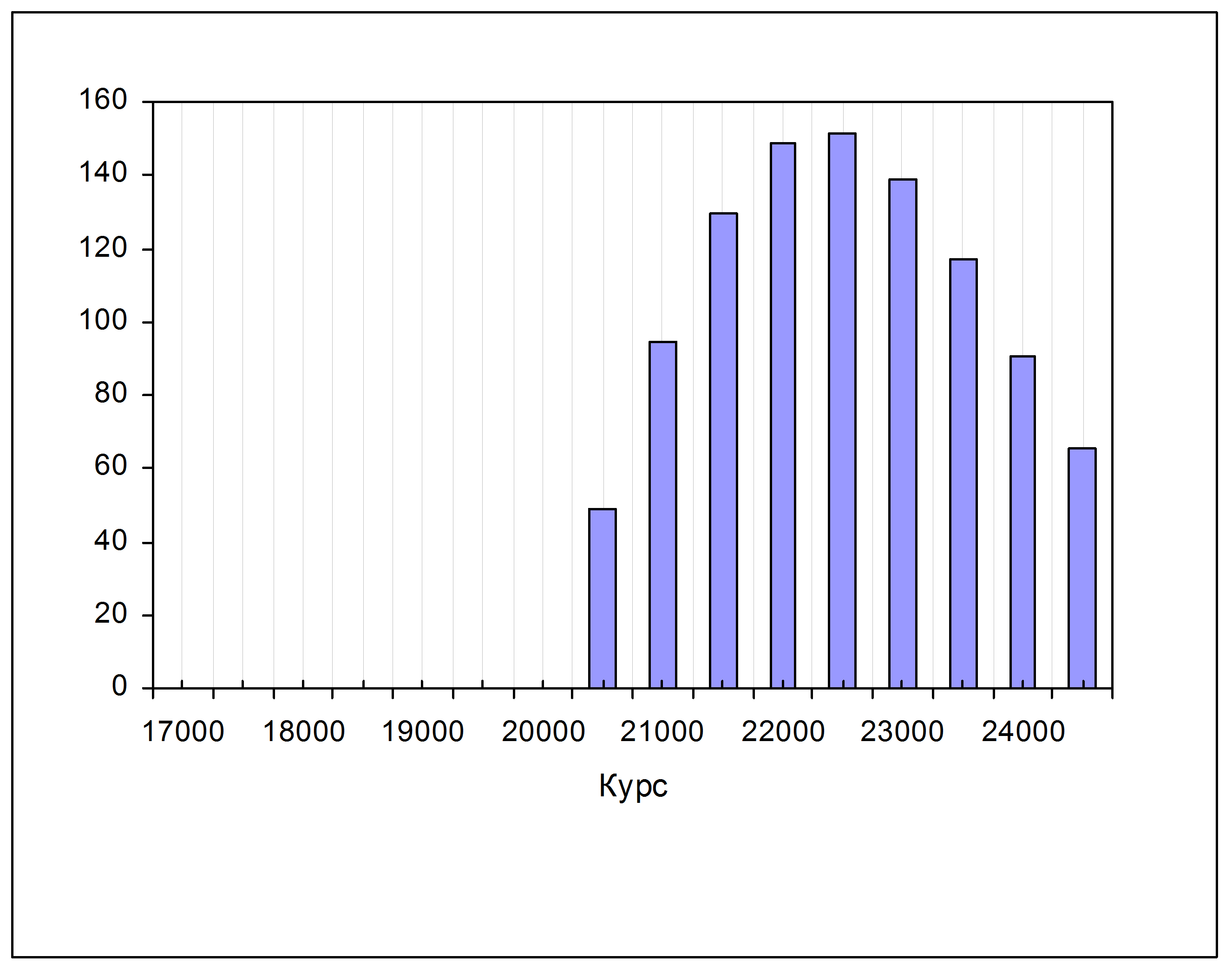
Видно, какой вклад в будущую стоимость дает каждое возможное значение цены. Хотя более высокие будущие цены дают большую стоимость опциона CALL, но вероятность их появления ниже, поэтому столбцы на результирующей гистограмме сначала возрастают, а потом, по мере падения вероятности – убывают.

Далее мы должны все столбцы просуммировать и это даст нам ожидаемое значение выплат по опциону CALL.

Это ожидаемое значение есть будущие наиболее вероятные выплаты. Напомним, что стоимость опциона CALL после этого получается приведением будущей стоимости к текущей стоимости путем дисконтирования на экспоненту с безрисковой ставкой R и со сроком T.

Впервые такую задачу решил Самюэльсон, а за ним Мертон, Фишер и Блэк. Формула для определения премии опционов европейского стиля на акции называется именами Блэка и Шоулза: 

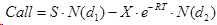
Где N(x) – интегральная функция нормального или Гауссового распределения с единичной дисперсией и нулевым средним, а ее аргументы определяются так:

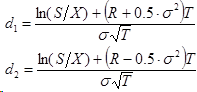
Присутствующий в формулах подгоночный параметр сигма ассоциируется с волатильностью базисного актива. Формула для премии опционов PUT выводится из принципа отсутствия арбитража, которое в случае опционного рынка называется правилом паритета опционов PUT и CALL:

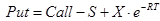
В какие предположения выведены эти формулы?

• Торговля БА ведется непрерывно, а поведение цены БА подчиняется модели геометрического броуновского движения с известными параметрами.
• По базисному активу дивиденды не выплачиваются в течение всего срока действия опциона.
• Нет транзакционных затрат, связанных с покупкой или продажей акции или опциона.
• Краткосрочная безрисковая процентная ставка известна и является постоянной в течение всего срока действия опциона.
• Любой покупатель ценной бумаги может получать ссуды по краткосрочной безрисковой ставке для оплаты любой части ее цены.
• Короткая продажа разрешается без ограничений, и при этом продавец получит немедленно всю наличную сумму за проданную без покрытия ценную бумагу по сегодняшней цене.