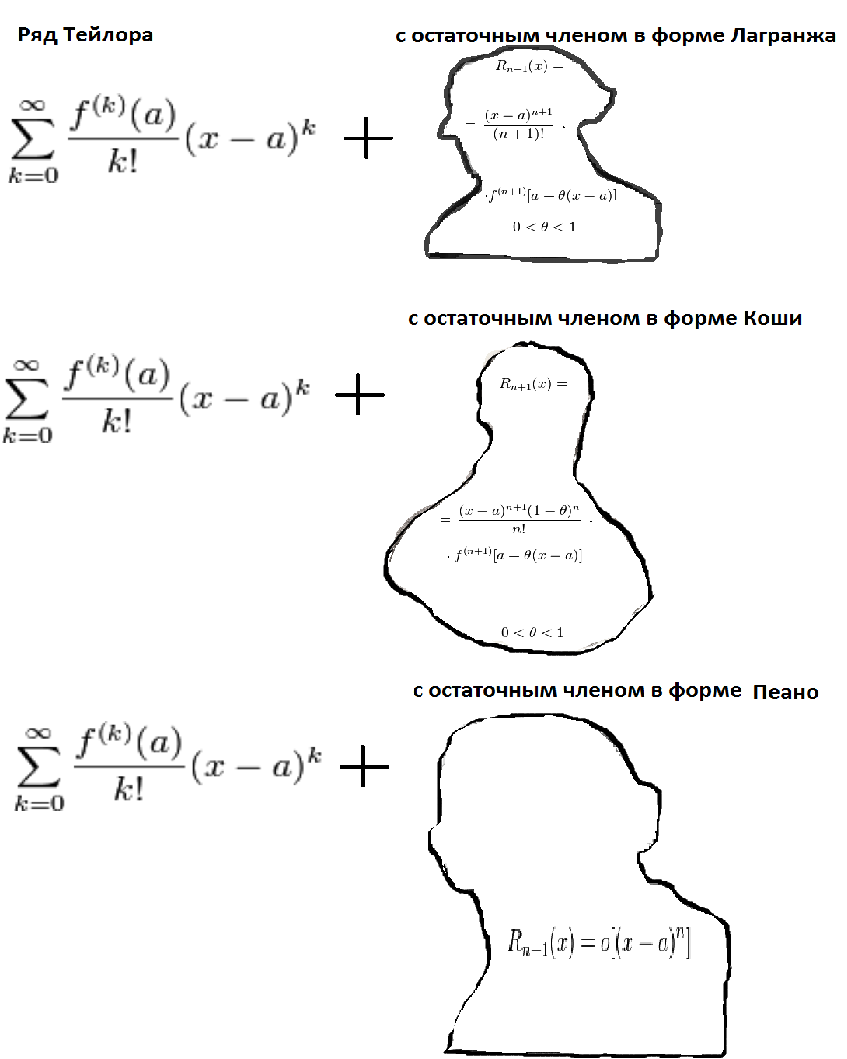
Формула Тейлора С Остаточным Членом В Форме Лагранжа
💣 👉🏻👉🏻👉🏻 ВСЯ ИНФОРМАЦИЯ ДОСТУПНА ЗДЕСЬ ЖМИТЕ 👈🏻👈🏻👈🏻
Формула Тейлора С Остаточным Членом В Форме Лагранжа
T
2
k
+
1
(
x
)
=
x
−
x
3
3
!
+
x
5
5
!
−
x
7
7
!
+
…
+
(
−
1
)
k
x
2
k
+
1
(
2
k
+
1
)
!
.
Рис. 22.1: Приближение
sin
x
тейлоровскими многочленами
T
n
(
x
)
=
(
x
−
1
)
−
(
x
−
1
)
2
2
+
(
x
−
1
)
3
3
−
(
x
−
1
)
4
4
+
…
+
(
−
1
)
n
(
x
−
1
)
n
n
.
Рис. 22.2: Приближение
ln
x
тейлоровскими многочленами
Чтобы найти первую производную в нуле, нам придётся воспользоваться определением — просто так применить стандартные правила дифференцирования не получится, т.к. функция по-разному опрделена в нуле и вне нуля.
Вторую производную тоже нужно находить по определению:
f
′′
(
0
)
=
lim
Δ
x
→
0
f
′
(
Δ
x
)
−
f
′
(
0
)
Δ
x
.
(22.1)
f
′
(
x
)
=
e
−
1
/
x
2
(
−
1
x
2
)
′
=
e
−
1
/
x
2
(
−
x
−
2
)
′
=
−
e
−
1
/
x
2
⋅
(
−
2
x
−
3
)
.
f
′′
(
0
)
=
lim
Δ
x
→
0
2
Δ
x
−
3
e
−
1
/
Δ
x
2
Δ
x
=
lim
Δ
x
→
0
2
Δ
x
−
4
e
−
1
/
Δ
x
2
.
Дальше можно продолжать в том же духе. Каждый раз будет получаться 0. (Докажите, что это действительно так!)
Итак, мы получаем, что все производные
f
в нуле равны нулю. Это означает, что тейлоровский многочлен этой функции тождественно нулевой: для всякого
n
,
T
n
(
x
)
=
0
для всех
x
.
Функция
f
при этом принимает ненулевые значения при всех
x
≠
0
. То есть о стремлении
T
n
(
x
)
к
f
(
x
)
при
n
→
∞
нет и речи.
Рис. 22.3: Функция с нулевыми производными. Кажется, что вблизи нуля у неё целый отрезок нулевых значений, но это иллюзия:
f
(
x
)
≠
0
при
x
≠
0
. Просто она стремится к нулю о-о-очень быстро.
Подведём промежуточный итог. Тейлоровские многочлены приближают функцию, по которой они построены, вблизи точки
x
0
, то есть когда
x
→
x
0
. Но это не означает, что для фиксированного значения
x
,
T
n
(
x
)
будет приближаться к
f
(
x
)
при больших значениях
n
. Хотя часто это верно. Когда именно? Об этом — следующая теорема.
f
(
b
)
=
T
n
(
b
)
+
f
(
n
+
1
)
(
c
)
(
n
+
1
)
!
(
b
−
a
)
n
+
1
.
(22.2)
Замечание 1. Если
n
=
0
,
T
n
(
b
)
=
f
(
a
)
и формула (22.2) превращается в формулу (17.3) из лекции 17, то есть наша теорема — это обобщение теоремы Лагранжа о конечных приращениях.
∣
∣
∣
∣
f
(
n
+
1
)
(
c
)
(
n
+
1
)
!
(
b
−
0
)
n
+
1
∣
∣
∣
∣
≤
|
b
|
n
+
1
(
n
+
1
)
!
.
Этот результат очень важен для практики. Собственно, когда вы просите компьютер посчитать значение синуса в какой-то точке, вместо синуса он вычисляет значение соответствующего тейлоровского многочлена достаточно большой степени.
Для начала, обозначим остаточный член (каким бы он ни был) через
R
n
(
x
)
:
Выберем теперь
q
таким образом, чтобы
H
(
b
)
=
0
. В этом случае
Значит существует такая точка
c
2
∈
(
a
,
c
1
)
, что
H
′′
(
c
2
)
=
0
.
Так мы можем продолжить до
n
-й производной: условия теоремы Ролля будут выполняться для
n
-й производной включительно (в частности, мы явно потребовали, чтобы
n
-я производная была бы непрерывна на отрезке
[
a
,
b
]
). Значит найдётся такая точка
c
n
∈
(
a
,
c
n
−
1
)
⊂
(
a
,
b
)
, что
H
(
n
+
1
)
(
x
)
=
f
(
n
+
1
)
(
x
)
−
T
(
n
+
1
)
n
(
x
)
−
q
(
n
+
1
)
!
=
f
(
n
+
1
)
(
x
)
−
q
(
n
+
1
)
!
.
Рассмотрим движение с постоянным ускорением. Пусть в момент времени
x
=
a
мы находились в точке
y
0
и в этот момент скорость движения составляла
v
0
. Пусть также на всём промежутке времени, который нас интересует, ускорение равнялось
A
. Тогда закон движения задаётся следующим образом:
Слагаемое
A
2
(
x
−
a
)
2
показывает, насколько сильно мы отклоняемся от движения с постоянной скоростью
v
0
к моменту времени
x
.
Рассмотрим теперь некоторый другой закон движения
y
=
f
(
x
)
, уже не обязательно происходящий с равномерным ускорением. Мы приближаем его движением с постоянной скоростью:
Пусть ускорение непрерывно, то есть
f
′′
непрерывно на всём отрезке
[
a
,
b
]
. В каких-то точках оно достигает своего максимума
A
max
и минимума
A
min
, а также принимает все значения из отрезка
[
A
max
,
A
min
]
.
Если я стартую в точке
f
(
a
)
с начальной скоростью
f
′
(
a
)
и всю дорогу буду двигаться с максимально возможным ускорением
A
max
, к моменту
b
я попаду в точку
T
1
(
x
)
+
A
min
2
(
b
−
a
)
2
≤
f
(
b
)
≤
T
1
(
x
)
+
A
max
2
(
b
−
a
)
2
.
Пусть
A
непрерывно меняется от
A
min
до
A
max
. Тогда для какого-то значения
A
=
A
∗
,
Аналогичным образом можно доказать эту формулу для любого
n
— только вместо ускорения нужно будет брать
(
n
+
1
)
-ю производную
f
. Заметим, что наше доказательство использует схожие идеи: функцию
H
можно записать в виде
Остаточный член в форме Лагранжа | Формула Тейлора
Формула Тейлора с остаточным членом в форме Лагранжа
Формула Тейлора с остаточным членом в форме Лагранжа.
Ряд Тейлора — Википедия
Теорема. Формула Тейлора с остаточным членом в форме Лагранжа
Даем определения производной и дифференциала. Разбираем правила дифференцирования и выводим формулы производных для основных функций. Рассказываем о формуле Тейлора и правиле Лопиталя.
Формула Тейлора с остаточным членом в форме Лагранжа.
Формула Тейлора с остаточным членом в форме Пеано.
Разложение основных элементарных функций по формуле Тейлора.
Примеры разложения функций по формулам Тейлора и Маклорена.
Вычисление пределов с помощью формулы Тейлора.
φ
(k)
(
x
0
)={
0,
k!,
если k≠m,
если k=m.
(3)
(3)φ(k)(x0)={0,если k≠m,k!,если k=m.
Пусть функции
f(x)
f(x)
и
ψ(x)
ψ(x)
определены в
δ
δ
-окрестности точки
x
0
x0
и удовлетворяют следующим условиям:
φ(
x
0
)=
φ
′
(
x
0
)=…=
φ
(n)
(
x
0
)=0,
ψ(
x
0
)=
ψ
′
(
x
0
)=…=
ψ
(n)
(
x
0
)=0;
(4)
(4)φ(x0)=φ′(x0)=…=φ(n)(x0)=0,ψ(x0)=ψ′(x0)=…=ψ(n)(x0)=0;
φ(x)
ψ(x)
=
φ
(n+1)
(ξ)
ψ
(n+1)
(ξ)
.
(5)
(5)φ(x)ψ(x)=φ(n+1)(ξ)ψ(n+1)(ξ).
φ(x)
ψ(x)
=
φ(x)−φ(
x
0
)
ψ(x)−ψ(
x
0
)
=
φ
′
(
ξ
1
)
ψ
′
(
ξ
1
)
x
0
<
ξ
1
0
δ>0
такое, что функция
f(x)
f(x)
имеет в
δ
δ
-окрестности точки
x
0
x0
производные до
(n+1)
(n+1)
-го порядка включительно.
f(x)=f(
x
0
)+
f
′
(
x
0
)
1!
(x−
x
0
)+…+
f
(n)
(
x
0
)
n!
(x−
x
0
)
n
+
f
(n+1)
(ξ)
(n+1)!
(x−
x
0
)
n+1
.
(8)
(8)f(x)=f(x0)+f′(x0)1!(x−x0)+…+f(n)(x0)n!(x−x0)n+f(n+1)(ξ)(n+1)!(x−x0)n+1.
r
n
(x)=f(x)−
P
n
(x).
(9)
(9)rn(x)=f(x)−Pn(x).
r
n
(
x
0
)=
r
′
n
(
x
0
)=…=
r
(n)
n
(
x
0
)=0.
(10)
(10)rn(x0)=rn′(x0)=…=rn(n)(x0)=0.
φ(x)
ψ(x)
=
r
n
(x)
(x−
x
0
)
n+1
=
r
(n+1)
n
(ξ)
(n+1)!
=
f
(n+1)
(ξ)
(n+1)!
,ξ∈Δ,
(11)
(11)φ(x)ψ(x)=rn(x)(x−x0)n+1=rn(n+1)(ξ)(n+1)!=f(n+1)(ξ)(n+1)!,ξ∈Δ,
Функцию
r
n
(x)=
f
(n+1)
(ξ)
(n+1)!
(x−
x
0
)
n+1
rn(x)=f(n+1)(ξ)(n+1)!(x−x0)n+1
называют остаточным членом формулы Тейлора в форме Лагранжа. Формула
(8)
(8)
справедлива и при
x=
x
0
x=x0
.
f(x)=
1
n!
(x−
x
0
)
n
f
(n)
(ξ).
f(x)=1n!(x−x0)nf(n)(ξ).
x−
x
3
3!
0.
(12)
(12)x−x33!0.
sinx=x−
x
3
3!
+
x
5
5!
sin(ξ+5
π
2
),
sinx=x−x33!+x55!sin(ξ+5π2),
f(x)=
∑
k=0
n
f
(k)
(
x
0
)
k!
(x−
x
0
)
k
+o((x−
x
0
)
n
), x→
x
0
.
(13)
(13)f(x)=∑k=0nf(k)(x0)k!(x−x0)k+o((x−x0)n), x→x0.
r
n
(x)
(x−
x
0
)
n
=
r
(n−1)
n
(ξ)−
r
n−1
n
(
x
0
)
n!(ξ−
x
0
)
,
(14)
(14)rn(x)(x−x0)n=rn(n−1)(ξ)−rnn−1(x0)n!(ξ−x0),
x
0
<ξЧлен В Гавне Порно Онлайн
Смотреть Порно Биби Джонс
Порно Фото В Пижаме
Сексопильные Японки
Ахуенное Порево