El universo en una taza de café
4. La búsqueda de nuestro lugar en el universo. Los griegos
Página 9 de 24
A Aristarco le siguió Arquímedes, considerado por muchos el mejor matemático y científico de la Antigüedad y uno de los tres mayores matemáticos de la historia junto con Newton y Gauss. Inventó el estudio de la hidrostática, la mecánica estática y la picometría, y se le suele apodar el padre del cálculo integral y el padre de la física matemática.
¿Y qué es esto de la física matemática?
De vez en cuando aparece alguien cuestionando por qué creemos tan ciegamente en las ecuaciones matemáticas y pone en duda su utilidad porque, al fin y al cabo, sólo son números.
Las ecuaciones matemáticas que aplicamos a la realidad no consisten en meter unos cuantos números en una fórmula sacada de la manga, hacer una serie de operaciones y creerte lo que dicen. En realidad, estas ecuaciones que describen el comportamiento de las cosas son el resultado directo de observar un fenómeno físico y cuantificar el efecto de todas las variables que intervienen en su desarrollo.
Por ejemplo, imaginemos que tenemos una bola en el suelo y le damos una patada. Observaremos que llegará más o menos lejos en función de lo fuerte que la hayamos golpeado. Por algún motivo tenemos interés en saber anticipadamente a qué distancia va a desplazarse la bola, así que vamos a poner una en el suelo y empezar a darle puntapiés para ver lo que pasa.
Tras el primer empujón, medimos lo lejos que ha llegado. Apuntamos la distancia, la recogemos y volvemos a colocar la bola en la misma posición inicial. Ahora le imprimimos el doble de fuerza y vemos que llega el doble de lejos. Con este segundo intento podemos deducir que, al doble de fuerza, doble de distancia recorrida. Para comprobar nuestra hipótesis, empujamos la bola con la mitad de la fuerza del primer intento y vemos que se para a la mitad de la primera distancia. A falta de más experimentos, podemos concluir que la distancia a la que la bola se desplaza aumenta proporcionalmente con la fuerza del golpe.
Por supuesto, ésta es una versión simplificada de las variables que intervienen en un experimento de verdad. Si quieres ser más exacto, hay que tener en cuenta cosas como la fricción del suelo con la superficie de la bola, el rozamiento con el aire, la pendiente del suelo, etc. ¿Que en vez de llegar el doble de lejos al empujarla con el doble de fuerza, la bola llega cuatro veces más lejos? Entonces la relación entre las dos variables hubiera sido proporcional al cuadrado del golpe inicial.
Y ésta es la realidad tras las ecuaciones matemáticas que se usan en física. En el fondo, no son más que la manera de describir cómo se comporta el mundo después de observar en qué proporción afecta cada variable al resultado final.
La cuestión es que Arquímedes fue el primero en observar la realidad y cuantificarla de esta manera. Midiendo las relaciones entre varios fenómenos podía modelar matemáticamente cuánta agua desplazaba un barco al ser depositado sobre ella o la fuerza que iba a realizar una palanca. Una vez encontradas estas relaciones, la vida se ve facilitada bastante, ya que permiten ahorrar en esfuerzo y recursos al ser capaces de predecir con antelación lo que se necesitará para abordar un problema.
Por ejemplo, en el caso de las palancas, Arquímedes postuló que la relación entre las fuerzas aplicadas en cada extremo es igual a la relación entre las distancias del punto de aplicación de cada fuerza al pivote.
De esta manera, si tienes que mover una carga más pesada de lo que puedes desplazar con tus propias manos y conoces más o menos su peso, puedes calcular la longitud de la palanca que necesitarás para moverla o la fuerza que tendrás que aplicar para conseguirlo. Esto te permite saber, antes de empezar el trabajo, a cuántos amigos tendrás que llamar exactamente para que te ayuden y reduce la cantidad de gente a la que harías perder el tiempo porque al final su ayuda no hacía falta, así que podrán aprovechar ese rato para seguir haciendo cosas más productivas.

Arquímedes no aportó gran cosa a la astronomía. En sus escritos, sólo se refiere al cielo para desaprobar la teoría de Aristarco, alegando que va en contra de todas las enseñanzas, para variar. Parece que, en particular, a Arquímedes no le gustaba la idea de que Aristarco colocara las estrellas tan lejos.
DATO CURIOSO
En su libro El contador de arena, Arquímedes proponía un sistema para enumerar cantidades inmensas. Como narrativa, en esta obra intentaba calcular cuántos granos de arena cabrían en el universo y para ello tenía que conocer el volumen que el universo ocupa. Por supuesto, nadie tenía ni idea en aquella época, pero existían varias teorías sobre el tamaño del universo, entre ellas la de Aristarco. Arquímedes comentó al respecto que:
Sus hipótesis [las de Aristarco] son que las estrellas y el Sol permanecen quietas, que la Tierra da vueltas alrededor del Sol sobre la circunferencia de un círculo y que la esfera de las estrellas fijas, cuyo centro se encuentra también en el Sol, es tan grande que el círculo en el que supone que la Tierra da vueltas tiene la misma proporción respecto a la distancia a las estrellas fijas como el centro de la esfera tiene a su superficie.
Al final, llegó a la conclusión de que el universo mide 100 billones de estadios de diámetro y que se necesitarían 1063 granos de arena para llenarlo. 1063 equivale, simplemente, a un 10 seguido de 63 ceros. En unidades modernas, Arquímedes calculó que el universo tenía un tamaño de unos 2 años luz. Ésa es, en realidad, la mitad de la distancia a la que se encuentra la estrella más cercana a la Tierra, a 4 años luz de distancia. De hecho, el universo observable mide entre 46 y 47 mil millones de años luz de diámetro… Un poco más grande de lo que Arquímedes podría haber imaginado.
¿Y por qué cuento todo esto, si en realidad tampoco tiene mucho que ver con la astronomía? Porque El contador de arena se la considera la primera publicación académica de investigación y exposición de la historia.
Sigamos con la historia y, más concretamente, con alguien que aportó más a la astronomía que el señor Arquímedes.
EL 29 DE FEBRERO
Un poco más tarde llegó Eratóstenes, quien demostró que la Tierra tiene forma de esfera e incluso hizo una aproximación de su diámetro. Por supuesto, la idea de que vivimos en un planeta esférico ya había surgido antes (¿recordáis a Aristarco?), pero por primera vez llegó alguien que aportó pruebas para respaldar su hipótesis.
Pero retomemos el asunto de demostrar que el planeta es esférico.
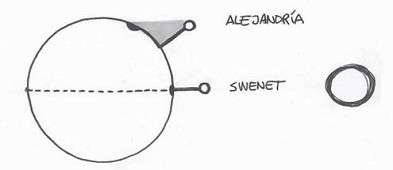
Eratóstenes vivía en Alejandría, pero había oído decir que en la ciudad egipcia de Swenet el Sol brillaba en el punto del cielo más alto posible, literalmente en el cénit, durante el mediodía del solsticio de verano. Por este motivo las cosas no proyectaban ninguna sombra en Swenet en ese preciso instante.
Pero Eratóstenes sabía que esto no ocurría en Alejandría el mismo día del año a la misma hora, así que observó la posición en la que se encontraba el Sol en su punto más alto, a mediodía, durante el solsticio de verano y descubrió que en Alejandría éste quedaba 7º 12’ al sur del cénit. La conclusión, para él, era obvia: la Tierra debía tener forma esférica.
DATO CURIOSO
Eratóstenes, además de inventar la disciplina de la geografía[25] con su obra Geographica, un tratado en el que describía todo el mundo habitado, llegó a ser el librero jefe de la biblioteca de Alejandría. Los funcionarios de esta biblioteca, la más importante de la Antigüedad, se tomaban tan en serio la misión de reunir la mayor cantidad de conocimiento posible que los barcos que llegaban a la ciudad tenían la obligación de dejarles los libros que trajeran consigo para que pudieran ser copiados. El resultado de tan concienzudo trabajo: una base de datos que se especula que albergaba entre 40.000 y 500.000 pergaminos en sus archivos.
Y digo albergaba porque, por desgracia para el futuro, la biblioteca fue consumida por el fuego. Las fuentes históricas que documentan su destrucción citan varias causas e incluso que no fue destruida en un solo incendio deliberado, sino en varios a lo largo de los años. La biblioteca pudo haber sido destruida por primera vez por Julio César en el año 48 a. C. y haber sufrido diversos destrozos hasta la conquista musulmana de Egipto en el año 642 d. C.
Si a veces nos cuesta recordar lo que hemos desayunado (el truco es desayunar siempre lo mismo), ya podéis ver lo difícil que es datar eventos que han tenido lugar hace más de un milenio y medio según los testimonios escritos por varias culturas. Todas ellas, probablemente, bastante poco imparciales.
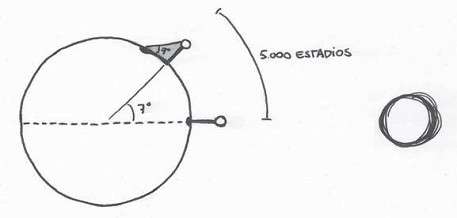
Eratóstenes también sabía que entre ambas ciudades existía una distancia de 5.000 estadios, una cifra obtenida a base de preguntar a mercaderes y viajeros cuánto tardaban en recorrer el camino entre ambas, así que con este dato ahora podría calcular las dimensiones del planeta.
Sabiendo que las dos ciudades estaban separadas por 7º 12’ y que la circunferencia de la Tierra, por ser esférica, tiene 360º, se puede deducir con una simple división que el ángulo entre Swenet y Alejandría representa una cincuentava parte de los 360º de la circunferencia terrestre. Por tanto, la circunferencia de la Tierra tenía que equivaler a 50 veces 5.000 estadios (la distancia entre ambas ciudades) o, lo que es lo mismo, 250.000 estadios.
Si bien el problema es que no sabemos con exactitud cuánto se acercó a la medida real del perímetro de la Tierra (que es de 40.008 kilómetros en el Ecuador), porque la longitud de los estadios variaba entre distintas culturas y no sabemos cuál de ellas usó Eratóstenes en sus cálculos. El valor que calculó podría estar entre 39.690 km y 46.620 km, lo que implicaría un error respecto al valor real de entre el 1,6 y el 16,3%.
En realidad, la aproximación a la cifra real es lo de menos. Incluso en el peor de los casos, su observación sirvió para demostrar definitivamente que la Tierra es esférica.
¡Eh! ¡No despaches el tema tan rápido, vaquero! ¡El Sol también proyectaría sombras con ángulos distintos en cada ciudad si la Tierra fuera plana!
Acompaño tu observación con una imagen, voz cursiva.

Sí, es verdad. No era suficiente basarse sólo en el experimento de Eratóstenes para afirmar con total seguridad que la Tierra era redonda. Pero existían otros fenómenos que otros filósofos ya habían observado con anterioridad y que respaldaban la teoría de la Tierra esférica. Por ejemplo, cuando alguien viaja largas distancias entre el norte y el sur algunas estrellas dejan de ser visibles y otras nuevas aparecen por el horizonte, lo que demuestra que estás desplazándote por una superficie curvada. Por otro lado, los griegos ya habían notado que los cascos de los barcos desaparecen tras el horizonte antes que los mástiles, lo que sólo puede ocurrir si se desplazan sobre una superficie curvada.
DATO CURIOSO
En realidad, la idea de que hasta hace poco la gente creía que la Tierra era plana tiene su origen en una campaña de desprestigio contra la Iglesia católica por parte de la Iglesia protestante en el siglo XVII. Desde el punto de vista de los protestantes, mucho más abiertos a las nuevas ideas y la ciencia que la doctrina católica, era una especie de insulto del estilo «¿Ah, sí? ¡Pues tu gente aún se piensa que la Tierra es plana!». La intención era mostrar desprecio porque, por supuesto, hacía dos mil años que todo el mundo sabía que no era así.
Pero, bueno, eso no quiere decir que no existan ejemplos recientes de gente que haya defendido que la Tierra es plana.
En 1906, el evangelista William Glenn Voliva sustituyó al antiguo pastor del pueblo de Zion, en Illinois (Estados Unidos). A su llegada, prohibió terminantemente fumar, beber, bailar o decir tacos, pero lo más llamativo fue su imposición en los colegios del pueblo de su propia doctrina que… Bueno, mejor reproduzco sus propias palabras:
La idea de un Sol de millones de millas de diámetro y a 91 millones de millas de distancia es ridícula. El Sol tiene un diámetro de 32 millas y no está a más de 3.000 millas de la Tierra. Es lógico pensar que sea así. Dios creó el Sol para iluminar la Tierra, y por tanto tiene que haberlo colocado cerca para cumplir la tarea para la que había sido diseñado. ¿Qué pensarías de un hombre que construye una casa en Zion y pone la lámpara para iluminarla en Kenosha, Winsconsin?
Dejando las curiosidades contemporáneas a un lado, volvamos a Grecia.
No contento con haber medido el diámetro de la Tierra, Eratóstenes se embarcó también en la misión de calcular la distancia a la que se encuentran la Luna y el Sol. De nuevo, sus cifras son polémicas porque no se sabe si la traducción original del texto en griego (σταδίων μυριάδας τετρακοσίας καί όκτωκισμνρίας, stadios miríadas tetrakosias kai oktokismirias) hace referencia a 400 estadios más 80.000 miríadas, que no es otra cosa que la manera que tenían los griegos de decir 10.000, lo que equivaldría a 4.080.000 estadios, o a 400 y 80.000 miríadas de estadios, es decir, 804.000.000 estadios.
Pero en cualquier caso, si la segunda interpretación fuera la correcta, entonces Eratóstenes de alguna manera habría predicho que la distancia al Sol es de unos 149 millones de kilómetros, una cifra que está sorprendentemente cerca del valor real de 149.597.870,7 kilómetros. Con la Luna no se acercó tanto, ya que calculó una distancia hasta ella de 780.000 estadios o 144.300 kilómetros, que es tres veces menos de lo que nos separa en realidad. También dijo que el Sol es 27 veces más grande que la Tierra, cuando la cifra real es 109 veces. La poca precisión de estos otros datos sugiere que también se equivocó con la distancia al Sol, dejándola en unos 22 millones de kilómetros.
Por otro lado, Eratóstenes fue el primero en dejar de lado los calendarios que dependían de la adición de meses al azar durante ciclos largos y complicados para que no se descuadraran las estaciones (os estoy mirando a vosotros, babilonios). Su gran innovación fue darse cuenta de que como cada año dura 365,25 días, bastaba con incluir un día extra cada cuatro años para paliar los efectos del día de retraso. Te damos las gracias, Eratóstenes, por habernos librado del sistema babilonio. ¡Hoy en día nuestros líderes no desatan el caos en los calendarios metiendo meses bisiestos cada dos por tres!
TODO GIRA EN TORNO A LA TIERRA, DE ESO NO HAY DUDA
Pese a que Eratóstenes pudo demostrar que la Tierra era esférica y calculó con bastante precisión su tamaño, no dejó de creer, al igual que el resto de los griegos en aquella época, que ésta era el centro del universo y que todo daba vueltas a su alrededor.
En tiempos de Erastótenes la teoría de que la Tierra se hallaba en el centro del universo estaba muy bien cimentada, sobre todo porque lo había dicho Platón, pero aun así la idea no quedó grabada con fuego en la conciencia de la gente hasta la llegada de Ptolomeo.
Ptolomeo vivió de los años 90 a 168 d. C., así que ya hemos superado la barrera del antes de Cristo.
En fin, Ptolomeo revolucionó el mundo de la astronomía escribiendo el Almagesto, un extenso tratado sobre el movimiento de los planetas y las estrellas en el cielo… Siempre desde la perspectiva geocéntrica, por supuesto. Sus postulados giraban alrededor de cinco principios básicos:
1. El reino celestial es esférico y se mueve como una esfera.
2. La Tierra es una esfera.
3. La Tierra está en el centro del cosmos, pero no en el centro exacto (como explicaré en un momento).
4. La Tierra, en comparación con la esfera de las estrellas, no tiene un tamaño apreciable y debe tratarse como un punto matemático.
5. La Tierra no se mueve.
En su modelo, basado en la idea de los epiciclos, los planetas, el Sol, la Luna y el firmamento se movían cada uno en su propia esfera, que a su vez contenía otra esfera alrededor de la cual también giraban. Esto explicaba fácilmente cómo algunos planetas podían cambiar de dirección durante su camino por el cielo. Hasta ahí puede parecer que no sugirió nada que Platón y Aristóteles no hubieran dicho ya, pero Ptolomeo añadió un pequeño detalle que mejoró mucho el sistema: no colocó la Tierra en el centro exacto del cosmos, sino un poco alejada de él.
Esta «solución» tan simple tenía su explicación. En el modelo geocéntrico en el que el Sol da vueltas alrededor de la Tierra en una órbita perfectamente circular, nuestra estrella se encuentra siempre a la misma distancia. El resultado de esto es que a lo largo del año todos los días deberían durar lo mismo y, bajo el punto de vista de los griegos, no debería haber cambios de estaciones porque la Tierra siempre recibiría la misma cantidad de calor. Podían solucionar este problema planteando que el Sol seguía una órbita elíptica alrededor de la Tierra en vez de circular, pero, claro, eso sería ir en contra de los círculos perfectos de Platón. Y todo lo que no eran círculos perfectos era impuro y no merecía la pena plantearlo.
Separando la Tierra del centro del cosmos, Ptolomeo consiguió el mismo efecto que conseguiría otorgando al Sol una órbita elíptica. El Sol no se encontraría siempre a la misma distancia que la Tierra y podría conservar su órbita circular.
Esto le servía de excusa para arreglar otro problema.
Las ideas de Platón obligaban a los astros no sólo a moverse en órbitas circulares, sino también a velocidades constantes e invariables. Por supuesto, esto no es lo que pasa en la vida real.
Como he explicado cuando hablábamos de Filolao, si se sigue el movimiento de los planetas a lo largo del año, veremos que éstos, además de ralentizarse y detenerse antes de cambiar de dirección, en ocasiones también aceleran repentinamente. Esto no sólo se debe a que desde nuestra perspectiva a veces adelantamos a otros planetas o éstos nos adelantan a nosotros, sino además a que se mueven a lo largo de órbitas elípticas. En el punto más cercano al Sol, los planetas son atraídos con más fuerza por su atracción gravitatoria y su velocidad se ve aumentada mientras que, a medida que se alejan, reducen la velocidad de nuevo.
Ptolomeo postuló que el movimiento de los planetas sí que es uniforme y perfecto, pero que lo es sólo respecto al punto opuesto a la Tierra, al otro lado del centro del universo. De esta manera, conservaba el movimiento platónico ideal, pero tenía la excusa de que desde la Tierra no podíamos apreciarlo debido a nuestra posición.
A este punto alrededor de lo que todo gira de manera uniforme lo llamó ecuante.
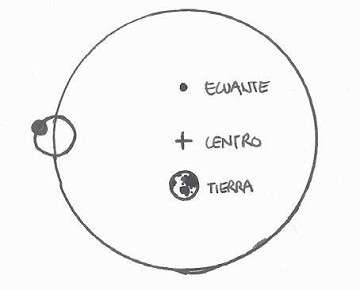
El sistema no era perfecto, pero podía predecir los movimientos de los planetas con una precisión muy respetable para la época y funcionaba mejor que cualquier otro modelo anterior. Dejando de lado las limitaciones que suponía tener que trabajar sólo con movimientos y formas perfectos a la hora de plantear una teoría, el concepto del movimiento uniforme de los astros respecto a un punto distinto a la Tierra para explicar sus cambios de velocidad era una manera muy inteligente de ajustar la teoría a las observaciones.
Usando las ideas de Platón y construyendo su modelo sobre el de Aristóteles (que, recordemos, era un berenjenal de 55 esferas celestiales), el sistema de Ptolomeo fue aceptado como verdad absoluta durante los siguientes doce siglos no sólo en Europa, sino también en el mundo musulmán.
La única pega de este sistema para explicar suficientemente bien las observaciones es que inducía a la gente a creer en la idea de que todo gira alrededor a la Tierra y, por tanto, de los seres humanos. Sobra decir que por aquel entonces mucha gente estaba demasiado cómoda con esta visión del universo y que frenaría cualquier intento por establecer un sistema distinto.