Эротосфена Решето

⚡ 👉🏻👉🏻👉🏻 ИНФОРМАЦИЯ ДОСТУПНА ЗДЕСЬ ЖМИТЕ 👈🏻👈🏻👈🏻

Все языки
Абхазский
Адыгейский
Африкаанс
Айнский язык
Акан
Алтайский
Арагонский
Арабский
Астурийский
Аймара
Азербайджанский
Башкирский
Багобо
Белорусский
Болгарский
Тибетский
Бурятский
Каталанский
Чеченский
Шорский
Чероки
Шайенского
Кри
Чешский
Крымскотатарский
Церковнославянский (Старославянский)
Чувашский
Валлийский
Датский
Немецкий
Долганский
Греческий
Английский
Эсперанто
Испанский
Эстонский
Баскский
Эвенкийский
Персидский
Финский
Фарерский
Французский
Ирландский
Гэльский
Гуарани
Клингонский
Эльзасский
Иврит
Хинди
Хорватский
Верхнелужицкий
Гаитянский
Венгерский
Армянский
Индонезийский
Инупиак
Ингушский
Исландский
Итальянский
Японский
Грузинский
Карачаевский
Черкесский
Казахский
Кхмерский
Корейский
Кумыкский
Курдский
Коми
Киргизский
Латинский
Люксембургский
Сефардский
Лингала
Литовский
Латышский
Маньчжурский
Микенский
Мокшанский
Маори
Марийский
Македонский
Коми
Монгольский
Малайский
Майя
Эрзянский
Нидерландский
Норвежский
Науатль
Орокский
Ногайский
Осетинский
Османский
Пенджабский
Пали
Польский
Папьяменто
Древнерусский язык
Португальский
Кечуа
Квенья
Румынский, Молдавский
Арумынский
Русский
Санскрит
Северносаамский
Якутский
Словацкий
Словенский
Албанский
Сербский
Шведский
Суахили
Шумерский
Силезский
Тофаларский
Таджикский
Тайский
Туркменский
Тагальский
Турецкий
Татарский
Тувинский
Тви
Удмурдский
Уйгурский
Украинский
Урду
Урумский
Узбекский
Вьетнамский
Вепсский
Варайский
Юпийский
Идиш
Йоруба
Китайский
Все языки
Абхазский
Адыгейский
Африкаанс
Айнский язык
Алтайский
Арабский
Аварский
Аймара
Азербайджанский
Башкирский
Белорусский
Болгарский
Каталанский
Чеченский
Чаморро
Шорский
Чероки
Чешский
Крымскотатарский
Церковнославянский (Старославянский)
Чувашский
Датский
Немецкий
Греческий
Английский
Эсперанто
Испанский
Эстонский
Баскский
Эвенкийский
Персидский
Финский
Фарерский
Французский
Ирландский
Галисийский
Клингонский
Эльзасский
Иврит
Хинди
Хорватский
Гаитянский
Венгерский
Армянский
Индонезийский
Ингушский
Исландский
Итальянский
Ижорский
Японский
Ложбан
Грузинский
Карачаевский
Казахский
Кхмерский
Корейский
Кумыкский
Курдский
Латинский
Лингала
Литовский
Латышский
Мокшанский
Маори
Марийский
Македонский
Монгольский
Малайский
Мальтийский
Майя
Эрзянский
Нидерландский
Норвежский
Осетинский
Пенджабский
Пали
Польский
Папьяменто
Древнерусский язык
Пушту
Португальский
Кечуа
Квенья
Румынский, Молдавский
Русский
Якутский
Словацкий
Словенский
Албанский
Сербский
Шведский
Суахили
Тамильский
Таджикский
Тайский
Туркменский
Тагальский
Турецкий
Татарский
Удмурдский
Уйгурский
Украинский
Урду
Урумский
Узбекский
Водский
Вьетнамский
Вепсский
Идиш
Йоруба
Китайский
        метод в теории чисел, назван по имени Эратосфена, заключающийся в отсеивании (например, путём зачёркивания) тех целых чисел заданной последовательности а1, a2,..., aN (например, натурального ряда чисел), которые делятся хотя бы на одно из простых чисел, меньших Nα (0 < α ≤ 1/2). Э. р. как теоретический метод исследования в теории чисел был введён в 1920 норвежским математиком В. Вруном.
Большая советская энциклопедия. — М.: Советская энциклопедия. 1969—1978.
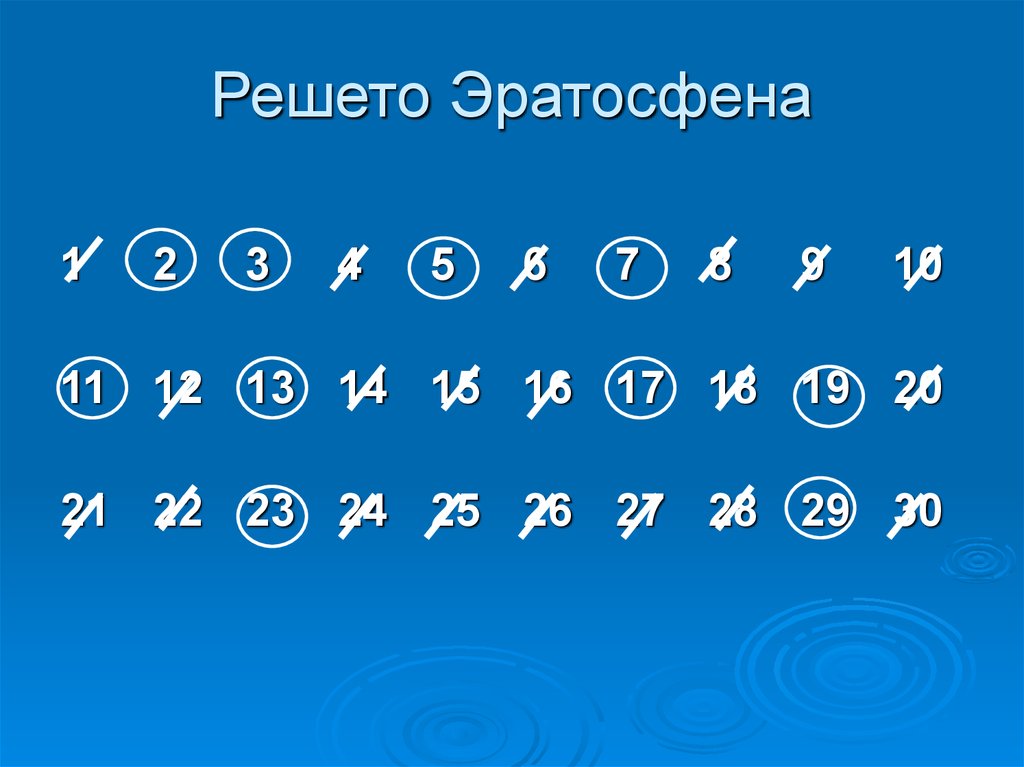
Эратосфена решето — Решето Эратосфена простой алгоритм нахождения всех простых чисел до некоторого целого числа n. Он был создан древнегреческим математиком Эратосфеном. Содержание 1 Пример для n = 20 2 См. также 3 Примеры реализации … Википедия
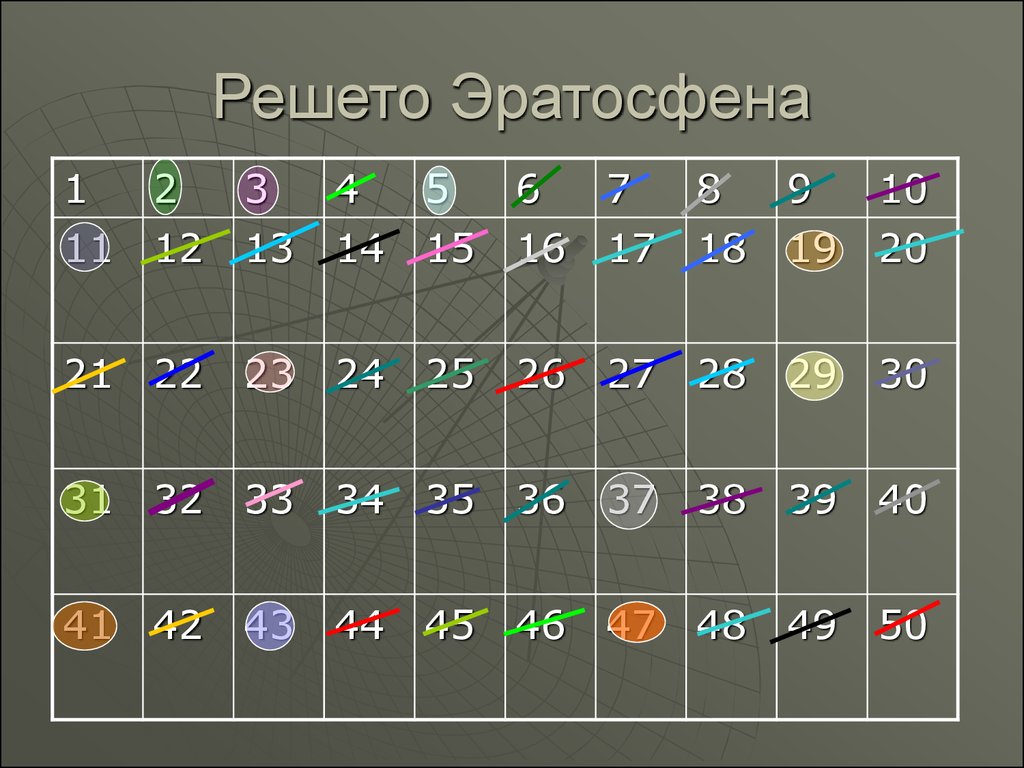
ЭРАТОСФЕНА РЕШЕТО — метод, разработанный Эратосфеном (3 в. до н. э.) и позволяющий отсеивать составные числа из натурального ряда. Сущность Э. р. заключается в следующем. Зачеркивается единица. Число 2 простое. Зачеркиваются все натуральные числа, делящиеся на 2.… … Математическая энциклопедия
Решето Аткина — В математике решето Аткина быстрый современный алгоритм нахождения всех простых чисел до заданного целого числа N. Основная идея алгоритма состоит в использовании неприводимых квадратичных форм (представление чисел в виде ax²+by²).… … Википедия
Решето Сундарама — В математике решето Сундарама детерминированный алгоритм нахождения всех простых чисел до некоторого целого числа . Разработан индийским студентом С. П. Сундарамом в 1934 году. Содержание 1 Описание 2 Обоснование … Википедия
Решето Эратосфена — алгоритм нахождения всех простых чисел до некоторого целого числа n, который приписывают древнегреческому математику Эратосфену Киренскому. Содержание 1 Алгоритм … Википедия
Решето Эратосфена — этим именем называют следующий способ получения ряда простых чисел. Из ряда чисел 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14... вычеркивают кратные двум; 4, 6, 8, 10, 12,... кратные трем: 6, 9, 12, 15,... кратные пяти: 10, 15, 20, 25, 30,...… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
БРУНА РЕШЕТО — один из решета методов в элементарной теории чисел, созданный В. Вруном [1]; является развитием Эратосфена решета. Метод Б. р. заключается в следующем: из последовательности натуральных чисел высеиваются (выбрасываются) числа с малыми простыми… … Математическая энциклопедия
Список алгоритмов — Эта страница информационный список. Основная статья: Алгоритм Ниже приводится список алгоритмов, группированный по категориям. Более детальные сведения приводятся в списке структур данных и … Википедия
Программируемые алгоритмы —     Служебный список статей, созданный для координации работ по развитию темы.  Данное предупреждение не устанавл … Википедия
Тест Миллера (теория чисел) — У этого термина существуют и другие значения, см. Тест Миллера. Не следует путать с «Тестом Миллера Рабина» вероятностным полиномиальным тестом простоты. Тест Миллера детерминированный полиномиальный тест простоты. В 1976 году Миллер… … Википедия
Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»

Включая результаты для "Эратосфена Решето".
Показывать только результаты для Эротосфена Решето?
https://ru.wikipedia.org/wiki/Решето_Эратосфена
Ориентировочное время чтения: 4 мин
Неограниченный, постепенный вариант
В этом варианте простые числа вычисляются последовательно, без ограничения сверху, как числа находящиеся в промежутках между составными числами, которые вычисляются для каждого простого числа p, начиная с его квадрата, с шагом в p (или для нечетных простых чисел 2p) . Может быть представлен символически в парадигме потоков данных как

используя нотацию
Неограниченный, постепенный вариант
В этом варианте простые числа вычисляются последовательно, без ограничения сверху, как числа находящиеся в промежутках между составными числами, которые вычисляются для каждого простого числа p, начиная с его квадрата, с шагом в p (или для нечетных простых чисел 2p) . Может быть представлен символически в парадигме потоков данных как

используя нотацию абстракции списков, где \ обозначает разницу между арифметическими прогрессиями.

Первое простое число 2 (среди возрастающих положительных целых чисел) заранее известно, поэтому в этом самореферентном определении нет порочного круга.

Псевдокод поэтапного отсеивания, в неэффективной, для простоты, реализации (ср. с нижеследующими вариантами):

Перебор делителей
Решето Эратосфена часто путают с алгоритмами, которые поэтапно отфильтровывают составные числа, тестируя каждое из чисел-кандидатов на делимость используя по одному простому числу на каждом этапе.

Широко известный функциональный код Дэвида Тёрнера 1975 г. часто принимают за решето Эратосфена, но на самом деле это неоптимальный вариант с перебором делителей (в оптимальном варианте не используются делители, большие квадратного корня тестируемого числа). В псевдокоде,

Сегментированное решето
Как замечает Соренсон, главной проблемой реализации решета Эратосфена на вычислительных машинах является не количество выполняемых операций, а требования по объёму занимаемой памяти (впрочем, его замечание относится к неактуальному сейчас компьютеру DEC VAXstation 3200, выпущенному в 1989 году). При больших значениях n, диапазон простых чисел может превысить доступную память; хуже того, даже при сравнительно небольших n использование кэша памяти далеко от оптимального, так как алгоритм, проходя по всему массиву, нарушает принцип локализованности ссылок .

Для решения представленной проблемы используется сегментированное решето, в котором за итерацию просеивается только часть диапазона простых чисел. Данный метод известен с 1970-х годов и работает следующим образом:
1. Разделяем диапазон от 2 до n на отрезки (сегменты) некоторой длины Δ ≤ √n.
2. Находим все простые числа в первом отрезке, используя обычное решето.
3. Каждый из последующих отрезков оканчивается на некотором числе m. Находим все простые числа в отрезке следующим образом:

Если число Δ выбрано равным √n, то сложность алгоритма по памяти оценивается как O(√n), а операционная сложность остаётся такой же, что и у обычного решета Эратосфена.

Для случаев, когда n настолько велико, что все просеиваемые простые числа меньшие √n не могут уместиться в памяти, как того требует алгоритм сегментированного сита, используют более медленные, но с гораздо меньшими требованиями по памяти алгоритмы, например решето Соренсона.

Решето Эйлера
Доказательство тождества Эйлера для дзета-функции Римана содержит механизм отсеивания составных чисел подобный решету Эратосфена, но так, что каждое составное число удаляется из списка только один раз. Схожее решето описано в Gries & Misra 1978 г. как решето с линейным временем работы (см. ниже).

Составляется исходный список начиная с числа 2. На каждом этапе алгоритма первый номер в списке берется как следующее простое число, результаты произведения которого на каждое число в списке помечаются для последующего удаления. После этого из списка убирают первое число и все помеченные числа, и процесс повторяется вновь:

Здесь показан пример начиная с нечетных чисел, после первого этапа алгоритма. Таким образом, после k-го этапа рабочий список содержит только числа взаимно простые с первыми k простыми числами (то есть числа не кратные ни одному из первых k простых чисел), и начинается с (k+1)-го простого числа. Все числа в списке, меньшие квадрата его первого числа, являются простыми.

В псевдокоде,

Решето только по нечётным числам
Поскольку все чётные числа, кроме 2, — составные, то можно вообще не обрабатывать никак чётные числа, а оперировать только нечётными числами. Во-первых, это позволит вдвое сократить объём требуемой памяти. Во-вторых, это уменьшит количество выполняемых алгоритмом операций (примерно вдвое).

Это можно обобщить на числа взаимно простые не только с 2 (то есть нечетные числа), но и с 3, 5, и т. д.

Уменьшение объёма потребляемой памяти
Алгоритм Эратосфена фактически оперирует с битами памяти. Следовательно, можно существенно сэкономить потребление памяти, храня переменных булевского типа не как байт, а как бит, то есть байт памяти.

Такой подход — «битовое сжатие» — усложняет оперирование этими битами. Любое чтение или запись бита будут представлять собой несколько арифметических операций. Но с другой стороны существенно улучшается компактность в памяти. Бо́льшие интервалы умещаются в кэш-память которая работает гораздо быстрее обычной так что при работе по-сегментно общая скорость увеличивается.

Решето Эратосфена с линейным временем работы
Этот алгоритм обнаруживает для каждого числа i в отрезке [2...n] его минимальный простой делитель lp[i] (lp от англ. least prime).

Также поддерживается список всех простых чисел — массив pr[], поначалу пустой. В ходе работы алгоритма этот массив будет постепенно заполняться.

Изначально все величины lp[i] заполним нулями.

Дальше следует перебрать текущее число i от 2 до n. Здесь может быть два случая:
• lp[i] = 0: это означает, что число i — простое, так как для него так и не обнаружилось других делителей.

Следовательно, надо присвоить lp[i] = i и добавить i в конец списка pr[].
• lp[i] ≠ 0: это означает, что текущее число i — составное, и его минимальным простым делителем является lp[i].

В обоих случаях дальше начинается процесс расстановки значений в массиве lp[i]: следует брать числа, кратные i, и обновлять у них значение lp[]. Однако основная цель — научиться делать это таким образом, чтобы в итоге у каждого числа значение lp[] было бы установлено не более одного раза.

Утверждается, что для этого можно поступить таким образом. Рассматриваются числа вида x = p ⋅ i, где p последовательно равно всем простым числам не превосходящим lp[i] (как раз для этого понадобилось хранить список всех простых чисел).

У всех чисел такого вида проставим новое значение lp[x] — оно должно быть равно p .

Псевдокод
https://e-maxx.ru/algo/eratosthenes_sieve
10.06.2008 · Решето Эратосфена . Решето Эратосфена — это алгоритм, позволяющий найти все простые числа в отрезке за операций.. Идея проста — запишем ряд …
https://dic.academic.ru/dic.nsf/bse/154360
Эратосфена решето — Решето Эратосфена простой алгоритм нахождения всех простых чисел до некоторого целого числа n. Он был создан древнегреческим математиком …
Занятие 14 Расширенный алгоритм Евклида Решето Эратосфена
Решето Эратосфена (часть 22) | Криптография | Программирование
Java. Решето Эратосфена. Проверка числа на простоту.
17.09.2015 · Решето Эратосфена Задачи и их решения / Решето Эратосфена Название алгоритма говорит о принципе его работы, то есть решето подразумевает фильтрацию, в …
https://ru.m.wikibooks.org/wiki/Реализации_алгоритмов/Решето...
В Википедии имеется статья по теме «Решето Эратосфена» Решето́ Эратосфе́на — алгоритм нахождения всех простых чисел, не превышающих некоторое натуральное …
https://ilovecalc.com/calcs/maths/eratosthenes-sieve/1278
16.11.2019 · Решето Эратосфена останавливается, когда квадрат числа, которое мы тестируем, больше, чем последнее число в сетке (в нашем случае 100). …
https://kvodo.ru/resheto-eratosfena.html
Решето Эратосфена. Вполне вероятно, что алгоритм, придуманный более 2000 лет назад греческим математиком Эратосфеном Киренским, был первым в своем роде.
https://scienceparadoxes.fandom.com/ru/wiki/Решето_Эратосфена
Решето Эратосфена — алгоритм нахождения всех простых чисел до некоторого целого числа ...
https://nsportal.ru/shkola/algebra/library/2015/09/15/resheto-eratosfena...
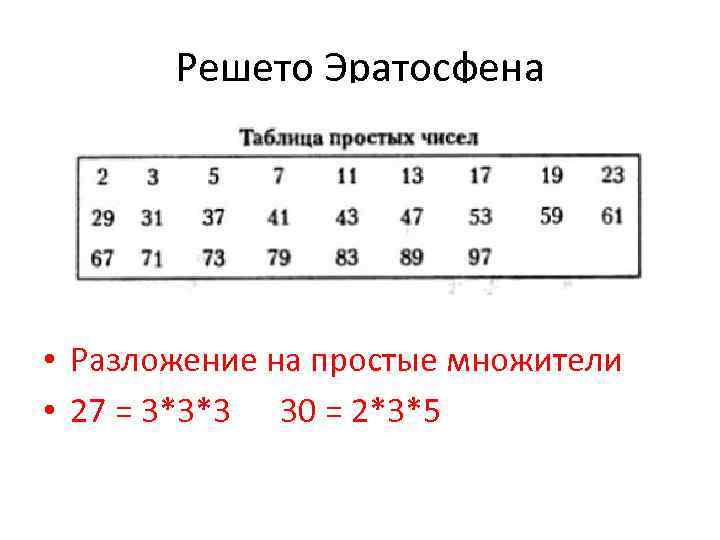
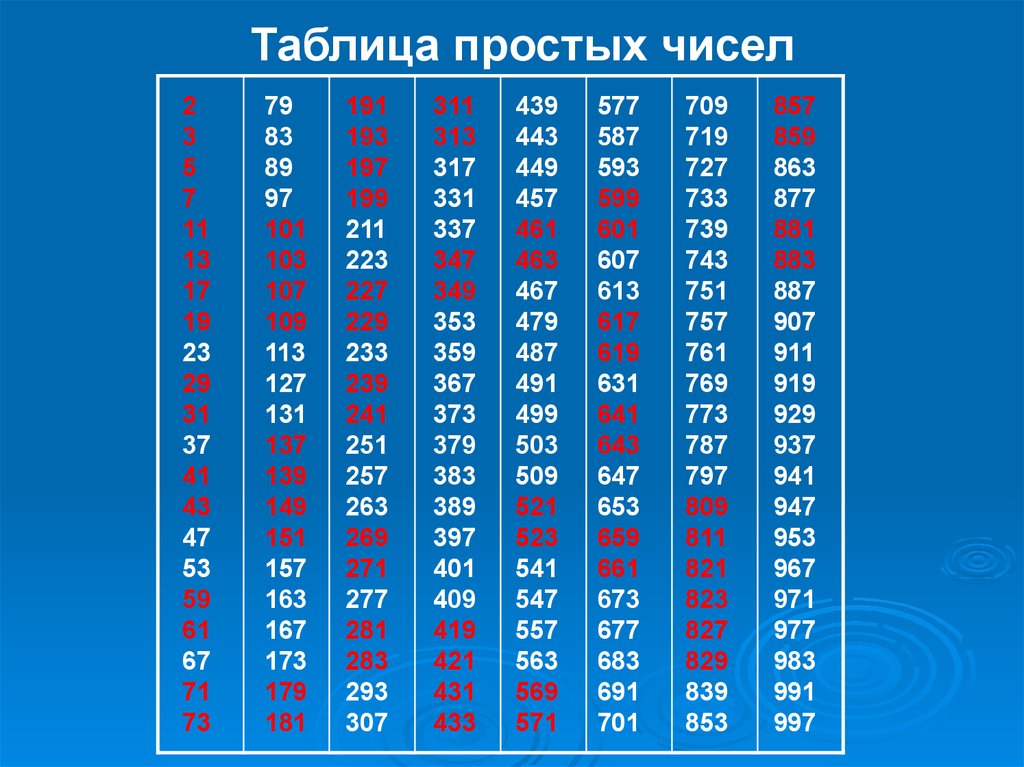
15.09.2015 · В арифметике Эратосфен стал вторым гроссмейстером (после Евклида). Он составил первую таблицу простых чисел («Решето Эратосфена») и заметил, что …
06.09.2011 · Решето Эратосфена с линейным временем работы . Дано число .Требуется найти все простые в отрезке .. Классический способ решения этой задачи — решето Эратосфена…
Не удается получить доступ к вашему текущему расположению. Для получения лучших результатов предоставьте Bing доступ к данным о расположении или введите расположение.
Не удается получить доступ к расположению вашего устройства. Для получения лучших результатов введите расположение.

Очко Сестри В Сперме
Негритянская Жопа
Сексопильные Японки
Фото Стоячих Членов Мужчин Крупно
Порнуха Видео Юные
Решето Эратосфена — Википедия
MAXimal :: algo :: Решето Эратосфена
Эратосфена решето - это... Что такое Эратосфена решето?
Решето Эратосфена
Реализации алгоритмов/Решето Эратосфена — Викиучебник
Решето Эратосфена - калькулятор онлайн | Математика ...
Решето Эратосфена. - Kvodo
Решето Эратосфена | Научные парадоксы Wiki | Fandom
Проект по алгебре (6 класс) на тему: Решето Эратосфена ...
MAXimal :: algo :: Решето Эратосфена с линейным временем ...
Эротосфена Решето