Деревья в SQL.Часть 2.
Coding
Множественная модель деревьев.
Множественная модель деревьев имеет некоторые свойства, которые я не упоминал в прошлом месяце.
Но сначала, давайте создадим таблицу для хранения информации о персонале. Я буду повсюду обращаться к этой таблице в остальной части этой статьи.
Дерево на рисунке 1(см. самый низ статьи) представлено как A) граф и Б) вложенные множества. Направление показываетя вложением, то есть Вы знаете, что кто-то - подчиненный кого-то еще в иерархии компании, если что левые и правые номера множества этого человека- между таковыми их боссов.
Другое свойство, которое я не упоминал в последний раз - то, что потомки- упорядоченны, т.е. Вы можете использовать номера элементов множества, чтобы упорядочить потомков.
Это свойство отсутствует в модели матрицы смежности, которая не имеет никакого упорядочения среди потомков.
Вы можете использовать этот факт при вставке, обновлении, или удалении узлов в дереве.
Одним из свойств дерева является то, что оно является графом без циклов. То есть никакой путь не замыкается, чтобы поймать Вас в бесконечной петле, когда вы следуете им в дереве. Другое свойство- то, что всегда имеется путь от корня до любого другого узла в дереве.
В модели вложенноых множеств, пути показываются как вложенные множества, которые представлены номерами множеств и предикатами BETWEEN.
Например, чтобы выяснить всех менеджеров, которым должен отчитываться рабочий, вы можете написать:
SELECT 'Mary', P1.emp, (P1.rgt - P1.lft) AS size FROM Personnel AS P1, Personnel AS P2 WHERE P2.emp = 'Mary' AND P2.lft BETWEEN P1.lft AND P1.rgt; Mary emp size ==== === ==== Mary Albert 27 Mary Charles 13 Mary Fred 9 Mary Jim 5 Mary Mary 1
Заметьте, что, когда size = 1, Вы имеете дело С Мэри как с ее собственным боссом. Вы можете исключить этот случай.
Модель вложенная множеств использует факт, что каждый вешний набор имеет больший size (size = right - left) чем множества, которые оно содержит. Очевидно, корень будет всегда иметь самый большой size.
JOIN и ORDER BY не нужны в модели вложенных множеств, как модели графа смежности. Плюс, результаты не зависят от порядка, в котором отображаются строки.
Уровень узла - число дуг между узлом и корнем. Вы можете вычислять уровень узла следующим запросом:
SELECT P2.emp, COUNT(*) AS level FROM Personnel AS P1, Personnel AS P2 WHERE P2.lft BETWEEN P1.lft AS P2 GROUP BY P2.emp; Этот запрос находит уровни среди менеджеров, следующим образом: emp level === ===== Albert 1 Bert 2 Charles 2 Diane 2 Edward 3 Fred 3 George 3 Heidi 3 Igor 4 Jim 4 Kathy 4 Larry 4 Mary 5 Ned 5
В некоторых книгах по теории графов, корень имеет нулевой уровнь вместо первого. Если Вам нравится это соглашение, используйте выражение "(COUNT(*)-1)".
Самообъединения в комбинации с предикатом BETWEEN- основной шаблон для других запросов.
Агрегатные функции в деревьях.
Получение простой суммы зарплаты подчиненных менеджера работает на том же самом принципе.
Заметьте, что эта общая сумма будет также включать зарплату босса:
SELECT P1.emp, SUM(P2.salary) AS payroll FROM Personnel AS P1, Personnel AS P2 WHERE P2.lft BETWEEN P1.lft AND P1.rgt GROUP BY P1.emp; emp payroll === ======= Albert 7800.00 Bert 1650.00 Charles 3250.00 Diane 1900.00 Edward 750.00 Fred 1600.00 George 750.00 Heidi 1000.00 Igor 500.00 Jim 300.00 Kathy 100.00 Larry 100.00 Mary 100.00 Ned 100.00
Следующий запрос будет брать уволенного служащего как параметр и удалять поддерево, расположенное под ним/ней.
Уловка в этом запросе - то, что Вы используете ключ, но Вы должны заставить работать левые и правые значения. Ответ - набор скалярных подзапросов:
DELETE FROM Personnel WHERE lft BETWEEN (SELECT lft FROM Personnel WHERE emp = :downsized) AND (SELECT rgt FROM Personnel WHERE emp = :downsized);
Проблема состоит в том, что после этого запроса появляются промежутки в последовательности номеров множеств. Это не мешает выполнять большинство запросов к дереву, т.к. свойство вложения сохранено.
Это означает, что Вы можете использовать предикат BETWEEN в ваших запросах, но другие операции, которые зависят от плотности номеров, не будут работать в дереве с промежутками.
Например, Вы не сможете находить листья, используя предикат (right-left=1), и не сможете найти число узлов в поддереве, используя значения left и right его корня.
К сожалению, Вы потеряли информацию, которая будет очень полезна в закрытии тех промежутков - а именно правильные и левые номера корня поддерева. Поэтому, забудьте запрос, и напишите вместо этого процедуру:
CREATE PROCEDURE DropTree (downsized IN CHAR(10) NOT NULL) BEGIN ATOMIC DECLARE dropemp CHAR(10) NOT NULL; DECLARE droplft INTEGER NOT NULL; DECLARE droprgt INTEGER NOT NULL; --Теперь сохраним данные поддерева: SELECT emp, lft, rgt INTO dropemp, droplft, droprgt FROM Personnel WHERE emp = downsized; --Удаление, это просто... DELETE FROM Personnel WHERE lft BETWEEN droplft and droprgt; --Теперь уплотняем промежутки: UPDATE Personnel SET lft = CASE WHEN lft > droplf THEN lft - (droprgt - droplft + 1) ELSE lft END, rgt = CASE WHEN rgt > droplft THEN rgt - (droprgt - droplft + 1) ELSE rgt END;END;
Реальная процедура должна иметь обработку ошибок, но я оставляю это как упражнение для читателя.
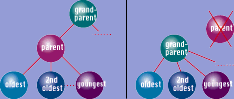
Удаление одиночного узла в середине дерева тяжелее чем удаление полных поддеревьев. Когда Вы удаляете узел в середине дерева, Вы должны решить, как заполнить отверстие.
Имеются два пути. Первый метод к повышает одного из детей к позиции первоначального узла (предположим, что отец умирает, и самый старший сын занимает бизнес, как показано на рисунке 2). Самый старший потомок всегда показывается как крайний левый дочерний узел под родителем.
Однако с этой этой операцией имеется проблема. Если старший ребенок имеет собственнх детей, Вы должны решить, как обработать их, и так далее вниз по дереву, пока Вы не добираетесь к листу.
Второй метод для удаления одиночного узла в середине дерева состоит в том, чтобы подключить потомков к предку первоначального узла (можно сказать, что мамочка умирает, и дети приняты бабушкой), как показано на рисунке 3. Это получается автоматически во модели вложенных множеств, Вы просто удаляете узел, и его дети уже содержатся в узлах его предка.
Однако, Вы должны быть осторожны, при закрытии промежутка, оставленного стиранием. Имеется различие в изменении нумерации потомков удаленного узла и изменения нумерации узлов справа. Ниже - процедура выполняющая это:
CREATE PROCEDURE DropNode (downsized IN CHAR(10) NOT NULL)
BEGIN ATOMIC
DECLARE dropemp CHAR(10) NOT NULL;
DECLARE droplft INTEGER NOT NULL;
DECLARE droprgt INTEGER NOT NULL;
--Теперь сохраним данные поддерева:
SELECT emp, lft, rgt
INTO dropemp, droplft, droprgt
FROM Personnel
WHERE emp = downsized;
--Удаление, это просто...
DELETE FROM Personnel
WHERE emp = downsized;
--Теперь уплотняем промежутки:
UPDATE Personnel
SET lft = CASE
WHEN lft BETWEEN droplft AND droprgt THEN lft - 1
WHEN lft > droprgt THEN lft - 2
ELSE lft END
rgt = CASE
WHEN rgt BETWEEN droplft AND droprgt THEN rgt - 1
WHEN rgt > droprgt THEN rgt -2
ELSE rgt END;
WHERE lft > droplft;
END;
Листинг 1
CREATE TABLE Personnel
(emp CHAR(10) PRIMARY KEY,
salary DECIMAL(8,2) NOT NULL CHECK(salary > = 0.00),
lft INTEGER NOT NULL,
rgt INTEGER NOT NULL,
CHECK(lft < rgt));
INSERT INTO Personnel VALUES ('Albert', 1000.00, 1, 28);
INSERT INTO Personnel VALUES ('Bert', 900.00, 2, 5);
INSERT INTO Personnel VALUES ('Charles', 900.00, 6, 19);
INSERT INTO Personnel VALUES ('Diane', 900.00, 20, 27);
INSERT INTO Personnel VALUES ('Edward', 750.00, 3, 4);
INSERT INTO Personnel VALUES ('Fred', 800.00, 7, 16);
INSERT INTO Personnel VALUES ('George', 750.00, 17, 18);
INSERT INTO Personnel VALUES ('Heidi', 800.00, 21, 26);
INSERT INTO Personnel VALUES ('Igor', 500.00, 8, 9);
INSERT INTO Personnel VALUES ('Jim', 100.00, 10, 15);
INSERT INTO Personnel VALUES ('Kathy', 100.00, 22, 23);
INSERT INTO Personnel VALUES ('Larry', 100.00, 24, 25);
INSERT INTO Personnel VALUES ('Mary', 100.00, 11, 12);
INSERT INTO Personnel VALUES ('Ned', 100.00, 13, 14);
Рисунок 1.
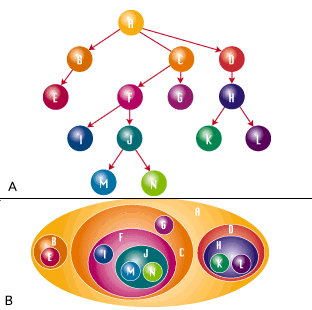
Рисунок 2.

Рисунок 3.