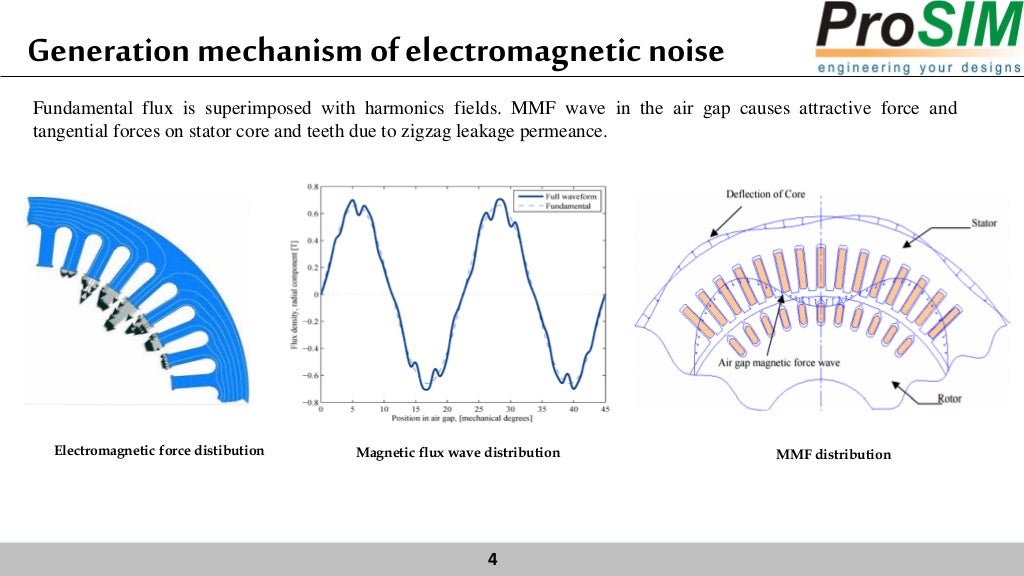
Coupled Analysis

👉🏻👉🏻👉🏻 ALL INFORMATION CLICK HERE 👈🏻👈🏻👈🏻

Coupled vs uncoupled analysis of one-way RC-slabs under nearby air explosions

The numerical techniques used for blast analysis of structures are categorized in “coupled” and “uncoupled” analysis methods. In a coupled analysis, the fluid–structure interaction is taken into account. Such analysis, although more accurate, is often complex and time consuming. In an “uncoupled” analysis, the blast loads are estimated by empirical equations and then applied to the structure in a separate analysis. Such an analysis is more cost effective, and of more interest for most practical design applications. The main objective of this study is to assess the efficiency of the empirical graphs prescribed by the UFC Code for uncoupled analysis of structures under the nearby air explosions of scaled distances between 0.4 and 0.7 kg/m1/3. The main characteristic of such explosions is the highly nonuniform distribution of blast-reflected pressure on the surface of structure. A method has been developed by the authors to address this nonuniform distribution in the uncoupled analysis. To examine the accuracy of analysis, the response values and the pattern of damages introduced on several reinforced concrete slabs under blast loads are compared with the results of a corresponding coupled analysis, and experimental observations. The uncoupled analysis described in this paper can be reasonably employed in the blast analysis and design of many structures.
Detonation of a high-explosive material results in a very rapid release of energy which often produces a significant light, heat, sound, and impulsive wave. The impulsive wave (i.e., a highly compressed spherical air that spreads outward from the source of explosion) may lead to catastrophic failure or progressive collapse and fragmentation. The numerical blast analysis of structures is categorized in “coupled” and “uncoupled” analysis methods. In a “coupled” analysis, the fluid–structure interaction (FSI) is taken into account. In fact, in addition to the structure itself, the finite-element model includes the explosive material (charge) and the air surrounding the structure in the analysis. The blast wave propagation and the structural response are coupled in such analysis. Therefore, it is required to account for interaction between the fluid (as a Eulerian material) and the solid domains in the finite-element analysis (Winget 2003). This requirement adds to the sophistications and cost of analysis. Alternatively, an “uncoupled” analysis may be employed in the response simulation of structures to blast loads as a more cost-effective analysis method. In an “uncoupled” analysis, the blast loads are evaluated with the aid of empirical equations and then applied separately on the structure. In fact, the fluid–structure interaction is eliminated in such analysis. An uncoupled analysis may be carried out in a static or a dynamic analysis approach. However, a coupled analysis is always a dynamic analysis. AUTODYN (2014) and LS-DYNA (Hollquist 2012) are two explicit dynamic finite-element software packages that have been successfully employed in both coupled and uncoupled blast response analysis of structures by many scholars.
A large number of research studies can be found in the literature, where in the response behavior of structures to blast loads or the impact of high-speed projectiles have been evaluated using the software packages mentioned in the previous paragraph. Given the focus of this paper, the recent studies relevant to the blast response of reinforced concrete (RC) slabs are reviewed as follows.
Zhou and Hao (2009) simulated the failure patterns induced in RC-slabs by contact detonations. Tai et al. (2011) examined the influence of the reinforcement ratio on the deflection and damage pattern of concrete slabs subjected to explosions of various charge weights. The dynamic response including the deflection and damages induced in RC-slabs to air explosions have been investigated by Kong et al. (2018), Yao et al. (2016), Zhao and Chen (2013), Wang et al. (2013), and Wei et al. (2007). Tham (2005) simulated the response of a RC-slab to the impact of a projectile, and concluded that the damage patterns at both sides of the slab were in good agreement with experimental observations. Nam et al. (2010) investigated the dynamic response of RC-slabs retrofitted by GFRP sheets through an experimental study that was followed by numerical simulation of the response. Li and Hao (2014) simulated the damages introduced in RC-slabs and RC-columns by explosives of various charge weights. Thiagarajan et al. (2015) investigated experimentally the central deflection and damages occurred in doubly reinforced concrete slabs using a shock tube to simulate the blast pressure. Dragos and Wu (2014) studied the interaction of direct shear and flexural deformations in the RC-slabs under blast loads. Xu et al. (2014) employed MATLAB (1996) to study the direct shear failure mode of RC-slabs under blast loads. Low and Hao (2002) studied numerically the shear and flexural failure modes of RC-slabs under blast loads. Koneshwaran et al. (2015) investigated the surface blast waves effect on tunnels buried under soil using two ALE and SPH numerical techniques. The response behavior of RC-slabs under blast loads has also been investigated by performing an uncoupled dynamic analysis on an SDOF model of the slab (Maazoun et al. 2018; Dragos and Wu 2014; Xu et al. 2014; Low and Hao 2002; Jones et al. 2009).
The response of structures in the research studies mentioned above has been either simulated by a coupled dynamic analysis (Zhao et al. 2018; Iannitti et al. 2018; Zhou and Hao 2009; Tai et al. 2011; Zhao and Chen 2013; Wang et al. 2013; Tham 2005; Koneshwaran et al. 2015) or an uncoupled dynamic analysis method (Yang et al. 2018; Wei et al. 2007; Nam et al. 2010; Li and Hao 2014; Thiagarajan et al. 2015). A coupled analysis usually leads to more accurate results; however, it is significantly more expensive and time consuming as compared to uncoupled analysis methods (Winget 2003). In the design of a structure to resist blast loads, it is not normally critical to control serviceability-related criteria such as deflection, crack width, and vibration. The primary design objective is to prevent catastrophic structural failure and hazardous fragmentations (Razaqpur et al. 2007). As such, uncoupled analysis methods are preferred in most design applications due to their lower computational complexity (UFC 2008). However, the accuracy of these methods may be highly affected by the flexibility of the target structure, the scaled distance, Z, of explosion, and the empirical equations that are used to evaluate both the magnitude of blast positive reflected pressure and the duration of the positive phase of blast pressure (UFC 2008).
The main objective of this paper is to examine the effectiveness of the uncoupled analysis method that is specified by the UFC Code (2008) in response analysis of RC-slabs under nearby air explosions with scaled distance values of 0.4 ≤ Z ≤ 0.7 kg/m1/3. Under such relatively small Z values, the distribution of blast-reflected pressure on the surface of structure will be highly nonuniform. A simplified approach is developed by the authors to account for this nonuniform distribution in the uncoupled analysis. The efficiency of the proposed simplified approach in improving the accuracy of the uncoupled analysis method prescribed by the UFC Code (2008) is examined through comparing the analysis results with the results of a corresponding coupled analysis, as well as previous experimental observations. The following section briefly introduces the RC-slabs that are investigated in this study.
The RC-slabs studied in this paper have been previously investigated in an experimental study conducted by Wang et al. (2013). Figure 1 illustrates the dimensions and reinforcing details of the slabs. The reinforcement includes a 75 × 75 mm mesh of steel rebars with 6 mm diameter in both x and y directions. The material properties of concrete are reported to be as follows: compressive strength = 39.5 MPa, tensile strength = 4.2 MPa, and Young’s modulus = 28.3 GPa. The yield strength and Young’s modulus of the reinforcing bars are 600 MPa and 200 GPa, respectively.
Geometry and the reinforcement of RC-slab test specimen (L = 1000 mm, h = 40 mm, d = 28 mm)
Table 1 contains the specifications and results of the tests carried out by Wang et al. (2013). As listed in this table, a total of 4 tests were conducted on the RC-slabs of identical dimensions. In each test, the RC-slab was placed horizontally on a special test setup, and the explosive material (TNT) was suspended above the center of the slab at a standoff distance of R = 400 mm. Given the different weight of the explosive material (W) used in each test, a different scaled distance (i.e., z = R/W1/3) for each test was calculated (see Table 1).
In the UFC Code (2008), the time history of blast-reflected pressure, Pr(t), is modeled conservatively as an idealized pressure–time blast load. As one of the objectives of current study is to compare the results of the uncoupled analysis with a corresponding coupled FSI analysis method, the time history of reflected pressure that is applied on the surface of the target structure is modeled using Eq. (1) as a more accurate equation (Friedlander 1946):
where parameters
P
rα
Prα
,
t
d
td
, and
t
A
tA
in Eq. (1) indicate the peak reflected pressure at an angle of incidence, α, the positive phase duration of blast pressure, and the time of arrival of blast wave, respectively. The coefficient b is a decay parameter defined as (Kinney and Graham 1985):
Equation (2) provides a reliable prediction for the decay parameter of blast loads (Wei et al. 2007). For a bulk of TNT material of weight
W
W
located at a standoff distance of R from the target structure, the value of parameters
P
rα
Prα
,
t
d
td
, and
t
A
tA
can be obtained using the UFC Code (2008).
This section deals with FE modeling of the experimental tests, as listed in Table 1. The response behavior of the RC-slabs to blast loads is simulated by both uncoupled and coupled finite-element (FE) dynamic analysis methods. The ANSYS AUTODYN software (2014) as an explicit non-linear finite-element program has been used for FE modeling of the RC-slabs. To examine the accuracy of FE analysis, the damage pattern and residual deflection at the center of the RC-slabs are simulated by the FE model and then compared with the experimental observations. The following subsections provide further details relevant to the FE modeling of the slabs.
In an uncoupled analysis, the reflected pressure on the slab is simulated by empirical methods. When a rigid slab is subjected to an explosion with a scaled distance value, Z, of greater than 3 m/kg1/3, one may assume a uniform distribution for the reflected pressure across the surface of slab (Wu et al. 2009). However, this assumption may not be reasonable for Z < 3 m/kg1/3.
A simplified method is developed to simulate the nonuniform distribution of the reflected pressure across the surface of a RC-slab. In the proposed method, the surface of slab is discretized into a set of square area segments of limited dimensions, as shown in Fig. 2. Next, a series of concentric arc circles are plotted such to intersect the area segments of the slab. The angle of incidence,
α
i
αi
, and the scaled distance, Zi, of each area segment i, are calculated using Eqs. (3) and (4), respectively:
where d represents the dimension of the area segment, and j is the order of the arc circle that intersects the area segment of interest. Parameters RA and Ri are the standoff distances of the explosive material from the center of slab and the area segment i, respectively. W is the total weight of explosive material.
Discretization of a ¼ of the RC-slab (L = 1000 mm, t = 40 mm, and d = 75 mm (into area segments to simulate nonuniform blast-reflected pressure
Having the scaled distance ZA (where ZA= RA/W1/3), and the angle of incidence,
α
i
αi
, evaluated for the area segment i, the peak reflected pressure at the given angle of incidence, and
P
rα
Prα
can be evaluated using the graphs provided by the UFC Code (2008). Furthermore, for any area segment i of scaled distance Zi, the time duration of positive phase of blast pressure,
t
d
td
, and the time of arrival of the blast wave,
t
A
,
tA,
can be evaluated by the UFC Code (2008). The decay parameter for any area segment i may be calculated using Eq. (2). Finally, the reflected pressure of the blast that is experienced by the area segment i is calculated using Eq. (1). On the basis of a sensitivity analysis carried out by Rasouli (2015), the area segments are selected to be squares of 75 × 75 mm in this paper.
A coupled analysis accounts for the nonuniform pressure distribution of blast loading in the analysis. Due to symmetry, only a quarter of the RC-slab, the explosive material, and the ambient air between the two are modeled in the finite-element (FE) analysis. In addition, the ambient air at the backward of concrete slab has been included in the finite-element model. The thickness of ambient air at the backward of the concrete slab is approximately twice of the maximum deflection expected to be experienced by the slab. This is to ensure that the deflected slab remains within the domain of the finite-element model. Figure 3 shows the 3D finite-element model of a quarter of the RC-slab in Test NRC-1, and the contour of air pressure at an early stage (approximately 0.4 ms) after detonation of the explosive material. As shown in this figure, the distribution of reflected pressure on the slab is nonuniform, as the fluid structure interaction is taken into account in the analysis.
Finite-element modeling of a ¼ of the RC-slab in Test NRC-1; a propagation of reflected pressure on the slab surface; b shockwave propagation in the air
Under blast loads, the mechanical properties of concrete will be significantly altered due to the high straining (loading) rate of material. Thus, it is quite essential to use a constitutive material model that addresses the high strain rate effects. The FE models presented in this paper employ the Riedel, Hiermaier and Thoma (RHT) (1999) dynamic damage model for the concrete material. The RHT model addresses various response mechanisms that are found in brittle materials. These include pressure and strain hardening, strain rate effects, third invariant dependence for compressive and tensile meridians, strain softening, and cumulative damage. The RHT model employs three strength surfaces which are: an elastic limit surface, a failure surface, and the remaining strength surface for the crushed material (Riedel et al. 1999). Figure 4 shows the strength surfaces of the model.
Strength surfaces defined for concrete material in the RHT model
The failure surface Y is defined as a function of pressure P, the load angle θ, and strain rate ἐ:
where
Y(p)=
f
c
[A(
P
∗
−
P
∗
spall
F
Rate
(
ε
,
)
)
N
]
Y(p)=fc[A(P∗−Pspall∗FRate(ε,))N]
, with
f
c
fc
being the compressive strength. Parameter A is a failure surface constant, N is a failure surface exponent, and
P
∗
P∗
is the pressure value normalized by
f
c
fc
, and
P
∗
spall
=
P
∗
(
f
c
/
f
t
)
Pspall∗=P∗(fc/ft)
. In addition,
F
Rate
(
ε
,
)
FRate(ε,)
is a function that accounts for the strain rates. The parameter
R(θ)
R(θ)
defines the third invariant dependency of the model as a function of the second and third stress invariants and a meridian ratio
Q
2
Q2
. The elastic limit surface is scaled from the failure surface:
where
F
e
Fe
is the ratio of the elastic strength to failure surface strength.
F
CAP(p)
FCAP(p)
is a function that limits the elastic deviatoric stresses under hydrostatic compression, varying within the range of (0, 1) for pressure between initial compaction and solid compaction pressures. A residual (frictional) failure surface is defined as
where B is the residual failure surface constant, and M is the residual failure surface exponent. Following the hardening phase, additional plastic straining of the material results in damage and strength reduction. Damage is accumulated by
where
D
1
D1
and
D
2
D2
are damage constants. The post-damage failure surface is then interpolated by
and the post-damage shear modulus is interpolated via
The strength and failure parameters adopted in this paper are as follows (AUTODYN 2014; Tu and Lu 2009): the reference density,
ρ
ρ
 = 2.75 g/cm3; shear modulus, G = 11.79 GPa; compressive strength,
f
c
fc
 = 39.5 MPa; tensile strength,
f
t
ft
 = 4.2 MPa; failure surface constant, A = 1.6; failure surface exponent, N = 0.61; meridian ratio, Q = 0.6805; the fractured strength constant, B = 1.6; the fractured strength exponent, M = 0.61; damage constants,
D
1
D1
 = 0.04, and
D
2
D2
 = 1,
ε
min
f
εfmin
 = 0.008; and residual shear modulus fraction is 0.13.
Concrete has a complex non-linear compression behavior because of its large-scale heterogeneity and a porosity of typically 10%. For this reason, the porous Equation of State (EOS) proposed by Herrmann (1969) is well adapted to capture the major macroscopic phenomena of concrete. In Herrmann’s p − 
α
α
model, the parameter
α
α
, which indicates the porosity of the material, is defined as
where
υ
υ
is the specific volume of the porous material and
υ
s
υs
is the specific volume of the material in the solid state at the same pressure and temperature. The magnitude of
υ
s
υs
is equal to 1/
ρ
s
ρs
at zero pressure, where
ρ
s
ρs
is the solid density of material which is the density at zero pressure of a fully compacted solid. The magnitude of
α
α
becomes unity when the material compacts to a solid. The compaction path,
α
α
(p, e), represents the volumetric stiffness of the porous material between initial compaction pressure
p
e
pe
and the fully compacted pressure
p
s
ps
as follows (Herrmann 1969):
In Eq. (12),
α
p
αp
is the porosity corresponding to the initial plastic yield, as shown in Fig. 5a, p is current pressure, and n is the compaction exponent, which can be 2 or 3 to allow for more flexibility to fit experimental data. In the present study, n is assumed to be 3. The solid EOS used here is polynomial, which has different analytic forms for states of compression and tension. The pressure is determined by compression after full compaction
μ
¯
μ¯
and specific internal energy e. The full compaction is defined as
μ
¯
=ρ/
ρ
s
−1
μ¯=ρ/ρs−1
, where
ρ
ρ
is density, and
ρ
s
ρs
is density at zero pressure and is related to full compaction (as shown in Fig. 5). For
μ
¯
>0
μ¯>0
, the material is under compression, and
For
μ
¯
<0
μ¯<0
, the material is under tension, and
Table 2 includes the default values of parameters used by AUTODYN (2014) for the eq
Naked Male Celebrity
Tits Dress
Bukkake Hd Sex
Natural Boobs Teen
Celebrity Hd Video
Coupled Analysis - an overview | ScienceDirect Topics
Coupled vs uncoupled analysis of one-way RC-slabs under ...
Coupled Structural/Thermal Analysis
Coupled Analysis | Scientific.Net
| Coupled Analysis - MIDASoft
Coupled analysis of floating wind turbines - DNV
Fully Coupled Analysis of an embankment during settlement
DNVGL-RP-0286 Coupled analysis of floating wind turbines
Coupled Analysis