Что за праздник Старый Новый Год?

Речь идёт о двух разных календарях. Первый — юлианский, он был введён на всей Римской Империи по указу Юлия Цезаря с 1 января 45 г. до Р.Х., его ещё называют «старым» стилем. Второй календарь — григорианский, узаконенный в 1582 г. римским папой Григорием XIII, или «новый» стиль.
Бытует мнение, что григорианский календарь является более правильным и точным, чем юлианский. Но говорить об этом столь же бессмысленно, как выяснять, какая единица измерения длины более истинная — вершок или дюйм: календарь — это просто система счисления больших промежутков времени.
Вместе с тем, установление календаря не является вопросом чисто техническим, поскольку связано в христианском мире с выбором дня празднования Христова Воскресения. А для него I Вселенским собором сформулировано следующее правило: Пасха празднуется в первый воскресный день, после первого полнолуния, которое наступит после первого равноденствия. Это значит, что Пасха должна попасть в особый день не только по солнечному, но и по лунному календарю, и эти календари должны быть как-то согласованы, т.е. по сути речь идёт о едином солнечно-лунном календаре.
В 325 году по решению Никейского собора весь христианский мир принял юлианский календарь. В то время день весеннего равноденствия приходился на 21 марта. Этот день был важной точкой отсчёта в определении дней христианских праздников, которые, в свою очередь, служили главными ориентирами в хозяйственном календаре.
Расчётная продолжительность года в юлианском календаре принимается ровно за 365 суток и 6 часов. На самом же деле Земля совершает свой оборот вокруг Солнца за немного меньшее время, и это время, хотя и очень медленно, но меняется. Его принято называть годом тропическим. В нашу эпоху средняя продолжительность тропического года равна примерно 365 суток 5 часов 48 минут и 45,2 секунды. В долях средних солнечных суток это составляет 365⁵²³¹³/₂₁₆₀₀₀, в десятичной записи примерно 365,2422. Однако, утверждение о том, что юлианский календарь отстаёт от точного времяисчисления на 11 минут в год, является распространённым научным суеверием.
Александрийские учёные-пасхалисты знали о расхождении юлианского и тропического годов: оно проявлялось, в частности, в том, что одно и то же положение Солнца, например, время весеннего равноденствия, постепенно сдвигалось на всё более ранние даты. Так, в годы земной жизни Христа оно попадало на 23 марта, а во времена I Вселенского собора 325 г. — уже на 21 число того же месяца. Именно поэтому они и положили включить в пасхальные вычисления условные расчётные даты, а не постоянно сдвигающиеся астрономические показатели: в этом проявилось их стремление привязать само время к годичному кругу служения Богу, а не к тварным светилам.
Сдвиг дня равноденствия в пределах единой человеческой жизни малозаметен: для юлианского календаря он составляет 1 сутки на 128 лет. Но к концу 16 века разница между астрономическим и расчётным равноденствием достигла уже 10 суток. И папа Григорий XIII (который сам был астрономом), вопреки постановлению Вселенского собора и несмотря на отрицательное отношение к этой затее многих учёных и католических клириков, включая польского астронома Николая Коперника (имевшего, как известно, духовный сан), провёл реформу календаря. Он «повелел», чтобы у католиков после 4 октября 1582 г. сразу наступило 15 октября, т.е. попросту выкинул из календаря 10 дней, со всеми памятными датами, днями рождений и проч. В Российской республике григорианский календарь в гражданский оборот был введён в 1918 г.; к этому моменту разрыв в календарях составлял уже 13 дней, и «не бывшими» были объявлены все дни с 1 по 13 февраля.
Отличие этих календарей состоит в счёте високосных лет. В юлианском календаре високосным является каждый четвёртый год, и исключения из этого правила нет. А в григорианском число високосных лет на протяжении четырёх столетий уменьшается на 3 по следующему правилу: если год делится на 4, то он високосный, но есть исключение: если он делится на 100, то не високосный, но есть исключение: если делится на 400, то всё же високосный. Так, 2000-й год попал под двойное исключение и был-таки високосным, а вот 2100-й по юлианскому календарю будет високосным, а по григорианскому не будет (делится на 100, но не делится 400), и разница с того момента на ближайшие 100 лет станет составлять уже 14 дней.
Григорианский календарь тоже длиннее тропического, но всего лишь на 26 секунд, расхождение в 1 сутки накапливается в нём за 3278 лет. Интересно, что папа Григорий свято верил в непогрешимость своего календаря и с гордостью написал в своей булле, что «отныне равноденствие и полнолуние никогда со своих мест не сдвинутся». Но сегодня мы хорошо знаем, что все три исходные движения, отмечающие ход времени — суточное вращение, лунный месяц и солнечный год — происходят вполне независимо друг от друга и не имеют наименьшего общего кратного, выражающегося приемлемым по величине числом. И потому во всех календарных расчётах всегда имеется некоторая неточность, которая неминуемо приведёт к нарастающему расхождению между ними и природными явлениями.
Немалая точность григорианским календарём, конечно, достигнута, то плата за неё довольно высока. Так, в григорианском летоисчислении разные столетия содержат разное количество суток, а в среднем григорианском столетии не содержится целого числа дней. Такие неравномерности и «подскоки» григорианского календаря исключают возможность его использования во многих случаях. Пересчёт из любого местного календаря (например, из лунного мусульманского или «звериного» китайского) для сопоставления с другими датами сперва всё равно производится в юлианский, и лишь после сопоставления с датой 1582 года — в григорианский.
И для александрийской пасхалии (для православных церквей, живущих по старому стилю), и для григорианской пасхалии (католических церквей и православных, принявших новый стиль) составлены специальные таблицы определения дня Пасхи. Для расчёта александрийской (православной старостильной) Пасхи имеется довольно простой алгоритм. Он основан на так называемом метоновом цикле (открытым афинским астрономом Метоном), состоящем в согласовании продолжительности лунного месяца и солнечного года: оказывается, с хорошей степенью точности (с погрешностью в несколько часов) 19 тропических лет равны 235 лунным месяцам. Это означает, что, с учётом високосного цикла юлианского календаря в 4 года и недельного цикла в 7 дней, александрийский календарь повторяется каждые 19‧4‧7 = 532 года.
Для расчёта православной Пасхи для года Y можно воспользоваться следующим простым правилом:
1) a = (19‧(Y mod 19) + 15) mod 30.
2) b = (2‧(Y mod 4) + 4‧(Y mod 7) + 6‧a + 6) mod 7.
Если (a + b) > 9, то Пасха приходится на (a + b – 9) апреля,
иначе — на (a + b + 22) марта ст. стиля.
Например, для 2024 года:
2024 mod 19 = 10;
a = (19‧10 + 15) mod 30 = 25;
2024 mod 4 = 0; 2024 mod 7 = 1;
b = (2‧0 + 4‧1+ 6‧25 + 6) mod 7 = 6;
(25 + 6) > 9, следовательно, православная Пасха (25 + 6 – 9) = 22 апреля по ст. стилю, или 5 мая по н. ст.
Для вычисления дня католической Пасхи можно воспользоваться алгоритмом, предложенным великим Гауссом:
1) A = Y mod 19;
2) B = Y mod 4;
3) C = Y mod 7;
4) K = Целая часть(Y mod 100);
5) P = Целая часть((13 + 8K) /25);
6) Q = Целая часть(K /4);
7) M = (15 – P + K – Q) mod 30;
8) N = (4 + K – Q) mod 7;
9) D = (19A + M) mod 30;
10) E = (2B + 4C + 6D + N) mod 7;
11) Дата Пасхи по новому стилю: 22 + D + E марта или D + E – 9 апреля.
Но есть 2 исключения:
если D = 29 и E = 6, то вместо 26 апреля будет 19 апреля,
если D = 28, E = 6 и (11M + 11) mod 30 < 19, то вместо 25 апреля будет 18 апреля.
Для 2024 года последовательно найдём:
A = 2024 mod 19 = 10;
B = 2024 mod 4 = 0;
C = 2024 mod 7 = 1;
K = Целая часть(2024 mod 100) = 20;
P = Целая часть((13 + 8‧20) /25) = 6;
Q = Целая часть(20 /4) = 5;
M = (15 – 6 + 20 – 5) mod 30 = 24;
N = (4 + 20 – 5) mod 7 = 5;
D = (19‧10 + 24) mod 30 = 4;
E = (2‧0 + 4‧1 + 6‧4 + 5) mod 7 = 5.
Католическая Пасха: (22 + 4 + 5) = 31 марта по н. ст.
Гаусс неоднократно корректировал этот алгоритм с 1800 по 1816 гг., находя сам и с помощью своего ученика Титтеля ошибки в нём. И, как видим, окончательный вариант получился не особо простым и понятным, содержащим к тому же исключения.
Католическая реформа календаря, проведённая папой Григорием XIII, была обусловлена позитивистским и рационалистическим стремлением уточнить «с помощью науки» то явление — календарь, которое помимо чисто утилитарного измерения имеет ещё и культурную и философско-религиозную составляющую. И в результате вместо «космической поэмы», имеющей ритмику (строгое повторение числовых характеристик) и цикличность (4-летний период), получилась «проза чисел» — «сухая бухгалтерия».
Но и в науке часто предпочтение отдают календарю юлианскому. Так, юлианский счёт жизненно важен в астрономии. Систему непрерывного счёта времени, связанную с повторяющимися природными явлениями, такими, как солнечные и лунные затмения, прилёты комет и др., разработал современник папы Григория XIII и решительный противник его нововведений французский учёный Жозеф Скалигер. С тех пор и поныне счёт дней в мировой научной хронологии производится в юлианской системе.
Ещё один интересный факт состоит в том, что юлианский календарь значительно ближе чем григорианский подходит к продолжительности оборота Земли вокруг Солнца, отмеренного относительно неподвижных звёзд (такой год называют сидерическим). Сидерический год связывает измерение времени со всем мирозданием, в то время как григорианский календарь — явление чисто земное. Длина юлианского года представляет собой среднюю величину между тропическим и сидерическим годами, и в этом сочетании космических ориентиров как бы символически отражается гармония космоса.
Интересно выяснить: существует ли календарь более простой, чем григорианский, но не менее точный? Ответ на этот вопрос можно получить, если использовать аппарат цепных дробей.
Разложим в цепную дробь продолжительность тропического года в солнечных сутках:
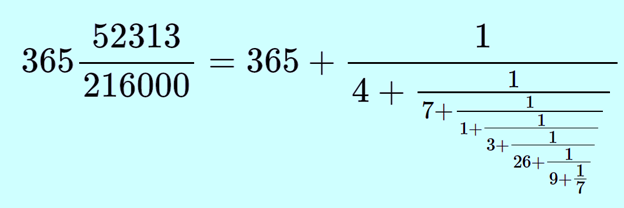
Числа, получаемые при «обрыве» цепной дроби, называют подходящими; они служат последовательными приближениями исходной дроби. Каждая из первых подходящих дробей даёт свой календарь:
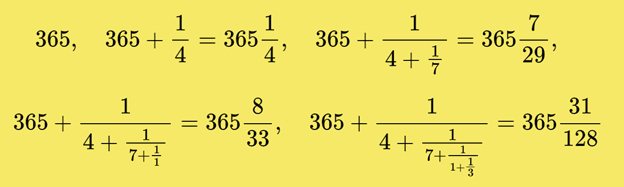
Последующие подходящие дроби имеют слишком большие знаменатели и по удобству мало отличаются от исходной дроби.
Представим результат в виде таблицы:
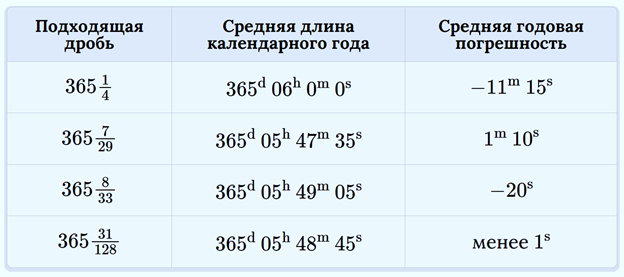
Правильные дроби в левом столбце сообщают главные свойства предлагаемого календаря. Знаменатель дроби — число лет в цикле. Если структуру календаря внутри цикла определять разделением на простые и високосные годы, то числитель дроби — это рекомендуемое число високосных лет в цикле.
Например, дробь 365¼ определяет юлианский календарь. Пользоваться приближением 365⁷/₂₉ никто не предлагал. Следующее приближение 365⁸/₃₃ даёт календарь почти той же сложности, но намного более точный, и более точный, чем григорианский! Использовать такой календарь (восемь високосных лет из каждых тридцати трёх) предлагал за полтысячелетия до григорианской реформы Омар Хайям (1048 —1131) — знаменитый поэт, математик и астроном. Как полагают, комиссия папы Григория XIII не пользовалась аппаратом цепных дробей.
Четвёртый вариант в 1864 году предложил немецкий астроном И. Г. фон Медлер. Этот календарь получается из юлианского по той же схеме, что и григорианский, но он даже проще: его цикл — 128 лет (а не 400), изменение количества високосных лет — минимальное — с 32 в юлианском до 31. Тем удивительнее, что этот календарь гораздо точнее — ошибка составляет менее 1 секунды!
Ещё один забавный факт, связанный с григорианским календарём. Если не принимать во внимание пасхалию (т.е. лунные циклы), то он имеет 400-летний цикл, содержащий 20871 неделю. За 400-летний цикл 13 число встретится 400‧12 = 4800 раз, но распределение по дням недели не будет одинаковым: понедельник встретится 685 раз, вторник — 685, среда — 687, четверг — 684, пятница — 688, суббота — 684, воскресенье — 687. Следовательно, за длительный период наблюдений среди тринадцатых чисел месяцев чаще других выпадает «пятница, тринадцатое». Такое расхождение в частотах связано с тем, что начало каждого цикла — вполне определённый день недели: понедельник (очередной цикл начался 1 января 2001 года).
Старый Новый Год — довольно интересное и самобытное явление, исключительно отечественное «изобретение». На Руси до революции, несмотря на все старания Петра I, Новый Год особо никто не праздновал — праздновали Рождество. Но когда Советская Россия стала отмечать Новый Год по григорианскому летоисчислению, как бы в пику этому событию возникла традиция, поддержанная церковью, встречать новолетие по «правильному» календарю. Ну и чисто психологически, в условиях затяжной зимы, можно понять стремление людей продлить ускользающие праздники.
Кстати, действительно имеется довольно большая несуразность в том, что Рождество (государственный праздник) идёт после Нового Года (государственного праздника). На самом же деле, само новое летоисчисление ведётся от Рождества (рождения) Богочеловека, но за отправную точку было принято не собственно появление на свет (25 декабря), а первое церковное событие, которое по этому поводу было совершено: согласно еврейскому закону восьмидневный младенец принял обрезание и был наречён именем Иисус. Этот восьмой день от рождения (1 января) и принят за начало нового летоисчисления. Наверное, можно иметь разные мнения о том, каким календарём лучше пользоваться, но трудно не согласиться с тем, что рождение всё же должно предшествовать обрезанию и наречению имени.