Честная игра?

В старинной индейской игре два игрока одновременно показывают один или два пальца. Если сумма чисел, показанная пальцами, чётна, то первый игрок выигрывает соответствующее число очков у второго — второй платит первому сумму, равную числу поднятых пальцев. Если же сумма нечётна, то, наоборот, второй выигрывает у первого сумму, соответствующую числу выкинутых пальцев.

Является ли эта игра честной? Как должен играть каждый игрок, чтобы обеспечить себе максимальный выигрыш?

Решение. Эта игра не является честной — она выгодна для второго игрока.

Обозначим первого игрока Р, второго Q. Матрица игры имеет вид:

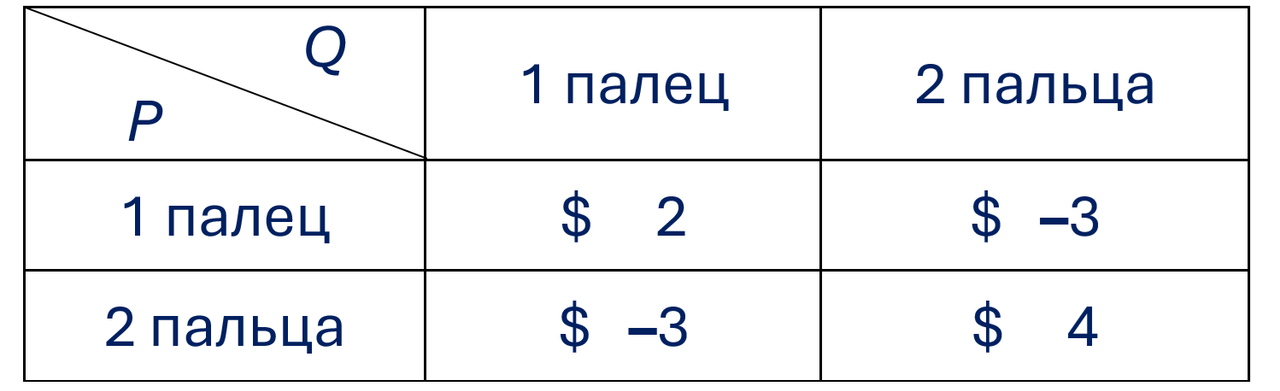
Предположим, что мы уже нашли оптимальные стратегии для обоих игроков, т.е. знаем, что лучшей стратегией для игрока Р является поднять один палец с вероятностью p₁ и два пальца — с вероятностью p₂ (очевидно, p₁ + p₂ = 1), и аналогично для Q наиболее выгодно поднять один палец с вероятностью q₁ и два пальца — с вероятностью q₂ (q₁ + q₂ = 1).

Поскольку оба игрока принимают решения независимо друг от друга, сумма денег, которую Q в среднем выплатит Р равна:

E = 2p₁q₁ – 3p₁q₂ – 3p₂q₁ + 4p₂q₂.

Игра была бы справедливой, если бы E = 0. Однако мы покажем, что  p₁ = q₁ = 7/12, p₂ = q₂ = 5/12, и тогда E = – 1/12.

Это означает, что Q выигрывает в среднем $1/12 после каждой игры, даже в том случае, если Р применяет оптимальную стратегию.

Подставим  q₁ = 1, q₂ = 0  в формулу для Е. Тогда E = Q₁ = 2p₁ – 3p₂. Аналогично, если q₁ = 0, q₂ = 1, то E = Q₂ = – 3p₁ + 4p₂. В этих обозначениях имеем: E = Q₁q₁ + Q₂q₂. Поскольку E — это средний проигрыш игрока Q, если он использует свою оптимальную стратегию,  Q₁ ≥ E  и Q₂ ≥ E, то

E = Q₁q₁ + Q₂q₂ ≥ q₁E + q₂E = (q₁ + q₂)E = E.

Поскольку ни q₁, ни q₂ не могут быть равны нулю, из предыдущего соотношения вытекает, что E = Q₁ = Q₂, т.е.

2p₁ – 3p₂ = – 3p₁ + 4p₂, откуда (вспоминая, что p₁ + p₂ = 1) имеем

p₁ = 7/12, p₂ = 5/12, и  E = – 1/12.

Аналогично, 2q₁ – 3q₂ = – 3q₁ + 4q₂, и, следовательно, q₁ = 7/12, q₂ = 5/12. Таким образом, доказано, что игра не является справедливой, и найдены оптимальные стратегии: для обоих игроков выгодно поднимать один палец с вероятностью 7/12.

Подставляя в формулу для среднего проигрыша второго игрока 1 – p₁ вместо p₂ и 1 – q₁  вместо q₂, получим:

E = 12p₁q₁ – 7p₁ – 7q₁ + 4.

Независимо от значения q₁ при p₁ = 7/12 имеем E = – 1/12. Аналогично, независимо от значения p₁ при q₁ = 7/12 имеем E = – 1/12. Таким образом, игроку всё равно, как играть, если он знает, что его противник использует оптимальную стратегию.

Данный парадокс разобран в книге Г.Секея «Парадоксы в теории вероятностей и математической статистике».