Алгоритмы поиска кратчайшего пути: Алгоритм Дейкстры

В прошлой статье мы рассмотрели алгоритм в поиска в ширину. Сегодня мы перейдем к следующему алгоритму поиска пути - алгоритм Дейкстры. Статья написана с расчетом на то, что вы прочитали предыдущую.

Здесь мы рассмотрим взвешенный неориентированный граф, который изображен ниже.

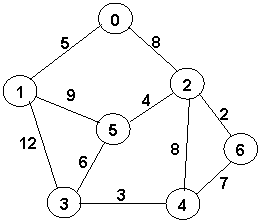
Алгоритм Дейкстры

В предыдущей статье я упоминал, что поиск в ширину очень важен и сейчас вы убедитесь в этом. Если вы разобрались с предыдущей статьёй, то алгоритм ниже для вас будет очевиден.

Единственное отличие алгоритма Дейкстры от поиска в ширину это наличие очереди с приоритетами. Приоритетом считается расстояние от начала пути до узла в очереди. Мы будем выполнять поиск лучшего (оптимального по расстоянию) пути.

Алгоритм выглядит следующим образом:

1. Добавляем первый узел в пустую очередь.
2. Удаляем из головы очереди узел и помечаем его текущим.
3. Помечаем узел как посещенный. Если узел тот, путь к которому мы искали, то останавливаемся.
4. Перебираем достижимые узлы из текущего.
5. Если достижимый узел не помечен как посещенный, то добавляем его в очередь в порядке приоритета и отмечаем, что достижимый узел достигнут из текущего. Заметьте, если в очередь был добавлен узел с расстоянием 5 от начала, а после этого узел с расстоянием 3 от начала, то второй узел окажется ближе к её голове, а значит на шаге 2 раньше покинет очередь.
6. Если очередь не пуста, то переходим к пункту 2.

Пример

Разберем поиск пути на графе выше из узла 0 в узел 3. Наша цель получить набор узлов по которым нам нужно пройти и при этом сумма весов рёбер, которые мы использовали была минимальна.

Добавим узел 0 в очередь.

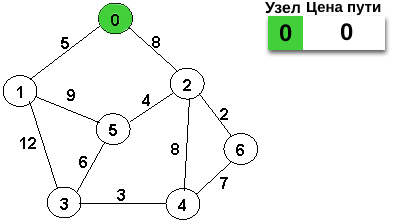
Удаляем из головы единственный узел, помечаем его посещенным и перебираем его соседние узлы. Добавляем их в очередь и упорядочиваем её по приоритету.

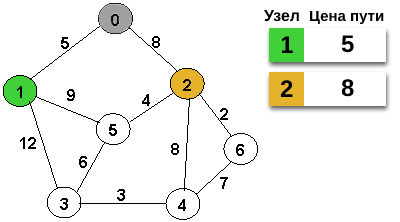
Очередь, не пуста и узел 1 - голова очереди, т.к. путь до него имеет минимальную длину 2.

Начнем обход соседей узла 1.

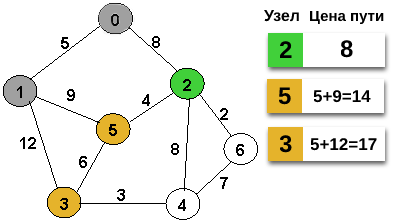
В результате добавления соседей, оказывается, что кратчайший необработанный путь на данный момент ведет к узлу 2. Это значит, что мы откладываем узлы 5 и 3 в порядке очереди и обрабатываем 2.

Обходим соседей узла 2 и при обходе обнаруживаем, что путь до узла 5 может быть обновлен до более короткого. Теперь мы можем достигнуть узла 5 через узел 2 с ценой 12 (8 + 4) и нам следует обновить очередь.

После обработки узла 2 мы оказываемся в ситуации, когда следуя алгоритму Дейкстры мы отдаляемся от финального решения. На очереди к обработке узел 6, но мы видим, что он не приведет нас оптимальному результату, однако, в такой ситуации хорошо справляется алгоритм А*, который мы разберем в следующей статье.

Начнем обработку узла 6. Из этого узла мы можем достигнуть вершины 4, однако это будет нам стоить 16 единиц, что хуже текущего известного решения, по этому мы не будем обновлять приоритет узла 4 в очереди.

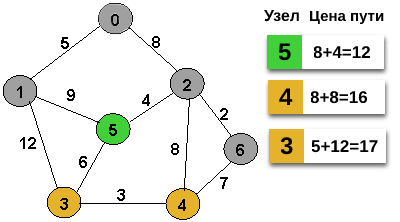
Путь из 5 в 1 мы не рассматриваем, т.к. узел 1 был уже обработан. Путь из узла 5 в узел 3 будет стоит 18 единиц (8 + 4 + 6). Это больше чем текущая стоимость пути в узел 3. Мы удаляем узел 5 из головы и на его месте оказывается узел 4.

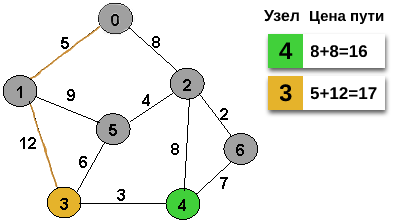
На графе выше обозначены оставшиеся узлы и лучший найденный путь из 0 в 3 на данный момент. При обработке узла 4 мы рассматриваем путь в узел 3. Цена этого пути 19 единиц, что больше текущего найденного пути через узел 1. Как вы видите, оптимальный маршрут был найден еще в самом начале, но только обработав весь граф мы смогли это доказать. Причина такого долгого поиска проста. Вес ребра между 1 и 3 равен 12 и это довольно сильный барьер для алгоритма, т.к. существует много других вариантов до которых добраться "жадным" способом быстрее.

Код алгоритма

Весь код вы найдете в репозитории по ссылке. В пакете demo расположены лаунчеры алгоритмов поиска пути, в пакете pathfinding расположены реализации алгоритмов. В пакете graph расположены реализации графов, а в пакете map - реализация простой игровой карты. Реализация алгоритма Дейкстры называется DejkstraSearch. Запустить поиск вы можете с помощью DejkstraSearchDemo.

Если код был вам полезен, вы можете поставить ⭐️ репозиторию и мне будет очень приятно.

Заключение

Сегодня мы с вами рассмотрели алгоритм Дейкстры, второй из трёх в нашем списке алгоритмов поиска пути. В следующей статье мы разберем отличия алгоритма А* и то, как он исправляет проблемы возникшие в нашем примере.

Исходники вы найдете в GitHub репозитории по ссылке.

Ссылки автора: Блог, GitHub