Алгоритмы. Обход дерева

Давно я не писал, как то все времени не находилось. Мы говорили про деревья, давайте теперь поговорим про обход деревьев. Обходы деревьев нужны собственно для того чтоб оптимально быстрой найти необходимый элемент в дереве.

Собственно обход дерева, как и все обходы графов ( а дерево это обычный неориентированный граф ) делается двумя методами: в глубину (Depth-first) и в ширину (Breadth-first).

Какой из методов использовать?

На самом деле споров достаточно много, и если зайти на различные форумы — то вы получите огромное количество ответов, каждый из которых не факт что будет полезен для вас. Потому, для себя я решил таким образом( взято кстати с треда на stackoverflow):

если вы знаете что решение где-то не далеко от вашей ноды — то лучше использовать обход в ширь, чтоб не закапываться глубоко в дерево
если дерево очень глубокое, а решение редки — то лучше все таки попробовать поиск в ширь
если дерево очень широкое, то можно попробовать поиск в глубь, потому как поиск в ширь может забрать слишком много времени.

Собственно, как я уже и писал, правильного ответа нет — потому надо пробовать разные варианты:) Эксперементировать всегда весело!

Так как мы будем пробовать на созданном бинарном дереве все алгоритмы, они редко бывают широкими, потому обсудим в начале поиск в глубь.

DFS. Алгоритмы в глубь имеют три типа обходов:

Pre-order

Pre-order стоит использовать именно тогда, когда вы знаете что вам нужно проверить руты перед тем как проверять их листья.

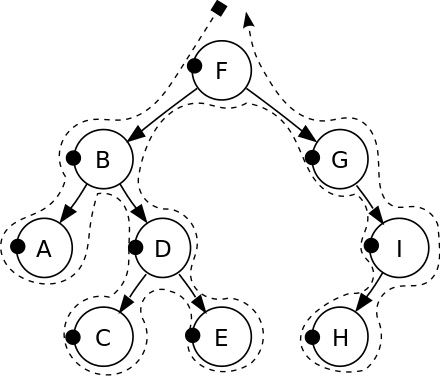
В результате Pre-order обхода мы получим такой порядок :

F, B, A,D,C,E,G,I,H

Код метода:

function preOrder(node){
  if (node == null) return;
  console.log(node.value);
  preOrder(node.left);
  preOrder(node.right);
}

2.In-order

In-order обход используется как раз когда нам надо проверять в начале детей и только потом подыматься к родительским узлам.

В таком случае мы получаем просто: A,B,C,D,E,F,G,H,I

function inOrder(node){
  if (node == null) return;
  inOrder(node.left);
  console.log(node.value);
  inOrder(node.right);
}

3.Post-order

Post-order самый забавный случай — это случай когда нам нужно начать-так сказать с листов и завершить главным узлом — тоесть разложить дерево на то, как оно строилось.

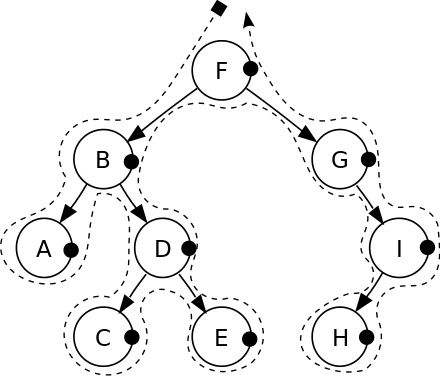
В таком случае мы полчаем: A, C, E, D, B, H, I, G,F

function postOrder(node){
  if (node == null) return;
  postOrder(node.left);
  postOrder(node.right);
  console.log(node.value);
}

Как видим — код очень похож:) просто разный порядок вызовов.

BFS.

BFS точно такой же как и в графах. Все достаточно просто — мы бегаем в начале по рут ноде, потом по всем ее детям, потом по всем детям детей, и так далее.

function bfs(node){
  var queue = [];
  var values = [];
  queue.push(node);
  while(queue.length > 0){
    var tempNode = queue.shift();
    values.push(tempNode.value);
    if (tempNode.left){
      queue.push(tempNode.left);
    }
    if (tempNode.right){
      queue.push(tempNode.right);
    }
  }
  return values;
}

Собственно на этом пока все:)

Как обычно: исходники примеров вы можете найти тут.

Источник: https://medium.com/@dimko1

Алгоритмы. Обход дерева

Report Page