Алгебраический подход к моделированию
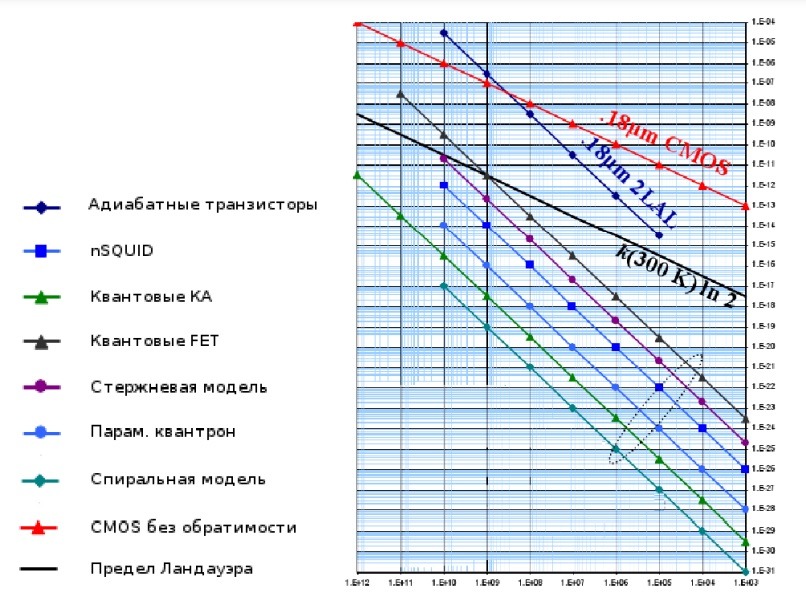
sergey shishkinТри барьера: График Эйсымонта

Выжимается ускорение грубой силой (количество процессоров) и технологическими трюками, Скорость света, Тепловыделение, Сложность программ.
Скорость света - Объективно ограничивает время вычислений снизу. Пока не видно возможности обойти этого зверя, но, если она появится, понадобится полная смена парадигмы.
Тепловыделение - Критическая проблема для суперкомпьютеров сейчас — выделение и отвод тепла. Затраты на энергию и охлаждение составляют большую часть стоимости.
Предел Ландауэра - Но одними технологическими ухищрениями не обойтись. Landauer, von Neumann: Термодинамическая нижняя граница для обработки информации. Обобщенный принцип Ландауэра — фон Неймана: Ediss > T × kB × ln P. kB постоянная Больцмана, T — абсолютная температура, P число состояний базового элемента. «Маленькая» тонкость - Ландауэр 1961: можно обойти предел, если наши действия обратимы. Bennett, 1973 Чтобы преодолеть предел Ландауэра, не только операции должны быть обратимы, но и управление тоже. Баллистические вычисления: автоматически развиваются, однажды стартовав. Все вычисления на молекулярном уровне и многие на нанокристаллическом обратимы. Квантовые вычисления обратимы. Сверхпроводящие вычисления обратимы. Так что никуда от обратимости не денемся.
Группы. Как представляют обратимые действия в науке? Группы: операция a ◦ b с единичным элементом e и обратными для каждого a−1: Ассоциативность: a ◦ (b ◦ c) = (a ◦ b) ◦ c; e ◦ a = a ◦ e = a; Обращение: a ◦ a−1 = a−1 ◦ a = e. Любое пространство обратимых функций — группа. Так что принято считать группы универсальным представлением обратимых операций.
Первые шаги в алгебру. Что вычисляет молекула или нанокристалл? Конечную группу. Так что с самого начала обратимые программы становятся недвоичными, нечисловыми, алгебраическими. Что в принципе можно алгебраически моделировать в конечных группах. Очень многое. Готова ли практика к этому? Нет. Готова ли теория к этому? Почти готова.
Гигатонны кода. Программные системы, как динозавры, задыхаются под тяжестью собственного кода. Считается, что процесс увеличения объема кода объективен. Объективно агрессивное невежество программистов.
Я изучал язык. Эффект агрессивного невежества проявляется уже для современных суперкомпьютеров. Разнородные процессоры и сложная топология не могут быть взяты топором-колуном C++∪MPI. Но программисты ИЗУЧАЛИ язык и он вбит им в голову как нечто абсолютное. Думать они могут лишь в терминах последовательных процессов и битов. Первые доклады о мире алгебраического программирования программисты практически не воспринимали . . . Это касается не только кодеров. Люди, занимавшиеся благородными Хаскеллом, Лиспом и Рефалом, тоже становились в тупик. А «железячники» быстро поняли, в чем суть.
Везде ли гигатонны? Математики (теоретические, чистые) уже давно и успешно борются с этим. Типичный случай развития новой математической теории — не разбухание под тяжестью новых никому не нужных пользователю и залатанных дыр, а свертывание первоначально длинных, сложных конструкций в простые ясные, но гораздо более абстрактные. Пример: теорема полноты классической логики. 200 страниц первоначального доказательства и пара страниц нынешнего, из которых лишь одна содержит конструкцию, а другая — необходимые понятия.
Но ведь это чисто техническая сложность, а не барьер? Барьер есть у каждого человека и сообщества: предел Чейтина. Чейтин (1968) установил, что каждая система (все равно, конечная или нет) не может понять объекты выше некоторой сложности. Переворачивать гигатонны — приближаться или превосходить свой предел Чейтина.
Как это делается? Д. Гильберт (1925): Хотя в принципе идеальные понятия могут быть устранены, наука не может без них развиваться. В некоторый момент бритва Оккама превращается в революционную бритву: гильотину. Это оставалось прозрением, не подтвержденным результатами, до 50-х годов.
Парадокс изобретателя. Д. Пойа: доказать простое утверждение часто можно лишь посредством сложных промежуточных лемм. Ван Хао (1954) В арифметике есть последовательность формул вида ∀x fn(x) = 0, где fi — элементарные вычислимые функции, для доказательства которых необходимы леммы с n переменами кванторов. В. Оревков (1968) Имеется последовательность формул логики An, такая, что для доказательства An без лемм необходимо 2 в степени 2 ... 2 (высота n) шагов, а для доказательства с леммами — 13 ∙ n + 7.
Пример эффекта Оревкова. Если у нас есть лишь исходная операция прибавления единицы, то вычисление экспоненты требует экспоненциального числа шагов. Если же записать ее неявное определение с помощью равенств ϕ(x, 0) = x + 1 и ϕ(x, y + 1) = ϕ(ϕ(x, y), y) то экспонента вычисляется в линейное число шагов.
Башня экспонент. Если теперь задать определение функции второго порядка Φ(ϕ, x, 0) = ϕ(0, x) и Φ(ϕ, x, y + 1) = Φ(ϕ, Φ(ϕ, x, y), y) то за линейное число шагов вычисляется уже суперэкспонента и так далее.
Возражение. Но ведь здесь рекурсия, и, более того, рекурсия по функциям над функциями! А как же накладные расходы на нее? Более аккуратным подбором примера (но при этом он значительно усложняется; см. например Митчелл 2010) можно избавиться от рекурсии; но функции высших порядков неустранимы.
Возражение 2. В примерах мы привязаны к конкретному объекту: натуральным числам. Избавляемся от чисел Идея примера взята из Митчелл 2010 Φ0 = f Φ1 = λf : (O → O)λx : O. f(f(x)). Φ1 в степени n (f)(x) = f(2 в степени n) (x). Φk+1 = λΨkλΨk−1. Ψk(Ψk(Ψk−1)).
Что может в принципе дать алгебраическое моделирование? Заменяя числа высокоуровневыми понятиями, можно сократить выкладки в башню экспонент раз (A. Оревков, 1968). Такой эффект в принципе недостижим грубой силой численных суперкомпьютеров. В алгебрах, основанных на бинарных операциях, функциональное программирование возникает с самого начала. Любой элемент a может рассматриваться как функция λx x ◦ a. Далее, соответственно, как преобразование функций.
Аналоговые вычисления? Алгебраические вычисления с самого начала естественно параллельны: каждый кристалл вычисляет свою групповую операцию независимо за один такт; разные кристаллы почти независимы. Это похоже на аналоговые компьютеры.
Единым махом. Таким образом, алгебраический подход одновременно атакует два барьера. А тогда, может быть, и что-то ещё? Да! Моделирование и теорию программирования.
Группы вместо дифуров. Как сейчас изучают дифуры в теории? Строят комплексы групп, описывающие их качественные свойства. Что нам нужно на практике? Чаще всего качественный ответ. Как он обычно получается? Переводим все на язык чисел, вычисляем. А затем пытаемся понять, что же содержательно получилось.
Числа избыточны??? Что следует из предыдущего? В принципе числа — избыточный промежуточный элемент. Почему же их везде используют? Привычно. Что же получилось? Числа стали идолом. “ Точное — то, что выражается числом” Рейтингопоклонничество и жертвы им уже приносят . . .
Обратимость
Влияние шума. Вероятность ошибки e в степени минус Esig/Ediss, Esig = 0.5 ∙ C ∙ V в степени 2. Формула энергии дана для электрического элемента. C — емкость элемента, V — разность напряжений при переключении, T — температура среды в градусах Кельвина. Для надежности нужно Esig > 100 ∙ T ∙ kB. Этот предел уже достигнут. А при делении ДНК имеем 40 ∙ T ∙ kB.
Споры вокруг Ландауэра. Доказательство — Plenio, Vitelli (2001). Опровержение — Norton (2004). Доказательство — Andrieux, Gaspard (2007). Доказательство — Ladyman et al (2007). Опровержение — Norton (2011).
И наконец эксперимент. Снайдер и другие (2012).

Три операции: копирование с сохранением информации, стирание с сохранением копии, стирание без копии.
Результаты эксперимента

Таким образом, подтверждена (правда, на самом простом случае: многократное повторение одной и той же операции) возможность обойти предел Ландауэра.
Теоретические расчеты
Обратимость с других точек зрения. Динамическая обратимость действий иллюстрируется моделью биллиардных шаров.
Любая динамическая система без диссипации по определению обратима.
Начинаются неприятности
А что же плохо? Могут групповые вычисления быть полны в смысле Тьюринга, как обычные языки программирования? Никогда. Можно ли иметь универсальную архитектуру обратимых процессоров для всех решаемых на них задач? Нельзя.
Аналогия с аналоговыми. Структура алгебраического процессора должна перестраиваться под задачу. Опять аналогия с аналоговыми машинами. Таким образом, в большинстве случаев алгебраический процессор должен быть специализированным устройством, работающим под управление традиционного. Таким образом, избавиться от чисел и битов не удастся. Но подвинуться их можно заставить.
Неприятности продолжаются. Можно использовать в алгебраическом программировании багаж накопленных численных алгоритмов? Почти ничего из него. И это хорошо, поскольку гарантирует от идиотских постановок задач типа ‘распараллелить существенно последовательную программу’.
О языках алгебраического программирования. Похож ли язык для алгебраического программирования на обычные? Совершенно другой. Можно ли переучить на алгебраическое тех, кто учился обычному? Ну, некоторые редкие личности способны понять совершенно новое . . .
Завершение постановки задачи. Подходят ли группы для описания действий обратимых программ и процессоров? Недостаточны. В соответствии с принципом баллистических вычислений Беннета, команды тоже должны обрабатываться обратимо. Есть естественная для обратимых процессоров и программ команда: взять обратный элемент или выполнить обратное действие (поменять вход и выход кристаллического элемента).
Проблема с обращением. Обращение может быть элементом группы лишь в случае. когда всегда a−1 = a (двоичная память из невзаимодействующих битов). Проваливается ассоциативность. Если M — элемент, осуществляющий обращение, то a ◦ (b ◦ M) не = (a ◦ b) ◦ M.
Назад к обычному программированию. На самом деле эта проблема возникает для обычных программ, но игнорируется в информатике. Рассмотрим команду UNDO. Тогда a; b; UNDO не то же, что {a; b}; UNDO. Так что нужен новый тип алгебр: алгебры программ.
Действия — не функции. В теории эффект операторов программ представляется как функция. Мы показали, что действия не могут так представляться. Они не образуют даже полугруппу, потому что не ассоциативны. Где подобный эффект наблюдался раньше? В функциональном программировании и комбинаторной логике. А мы показали, что он возникает даже в простейших языках скриптов. Но тем не менее в программе всегда есть структура полугруппы.
Предупреждение. Даже обратимые действия не обязательно дают обратимую программу. Пример: сборка кубика Рубика. Каждое действие обратимо, но информация об исходном состоянии безвозвратно теряется.
Некоторые выводы. Алгебраическое программирование и моделирование пробивает одновременно две стенки. Деться от него некуда. Люди, которые изучали языки программирования, переучиться на него не могут. Люди, которые овладевали системой знаний по информатике или математике — овладеть им иногда могут.
На что похожи обучавшиеся по стандартной методе? В принципе не могут выжить вне их горячего источника.
На что мы рискнули?
Формализм
Традиционные алгебраические представления. Любая полугруппа представляется как полугруппа функций, и, наоборот, любое пространство функций, замкнутое относительно композиции — как полугруппа. Глушков 1962 Maurer 1967 начинали с полугруппы и пополняли ее операциями алгоритмических языков. Обе этих линии развиваются до сегодняшнего дня.
Группоид. Мы установили, что действия, в отличие от функций, не всегда являются полугруппой. Можно гарантировать лишь бинарную операцию применения функции к аргументу (x * f). Этого достаточно для появления функционального программирования. a может рассматриваться как действие a: функция λx.(x * a). Далее как функция над функциями и т.п.
Использовались ли группоиды раньше? Стандартной алгебраизацией функционального программирования является комбинаторная алгебра. (x * (y * K)) = y; (x * (y * (z * S)) = ((x * y) * (x * z)). Её достаточно для выражения всех вычислимых функций и моделирования языков типа Lisp. Но к более абстрактным структурам не переходили.
Принципиальные недостатки комбинаторных алгебр. Барендрегт, предложение 5.1.15 Нетривиальные комбинаторные алгебры. Нетривиальные комбинаторные алгебры некоммутативны и не ассоциативны, бесконечны и не рекурсивны.
Чего не хватает в группоидах? Возможности создать сложное действие из простейших. Действие последовательности элементов a1, . . . , an: fa1, ..., an = λx.((x * a1) * ∙ ∙ ∙) * an). Не всегда действие последовательности выражается как действие одного элемента. Пример: алгебра «колодец, ножницы, бумага». Коммутативная с тремя элементами. (x * x) = x (w * p) = p (p * s) = s (s * w) = w.
Композиционный группоид. (f * ((g * (h * B)) = (f * (g * h)). Превращается в полугруппу, если задать дополнительное тождество. (f * ((g * (h * B)) * B)) = ((f * (g * B)) * (h * B)). Следствие: любой группоид вложим в полугруппу. Если группоид рекурсивен, то и эта полугруппа рекурсивна.
General algebraic program structure (GAPS)). Бигруппоид с ассоциативной операцией ◦ (последовательное исполнение) и не ассоциативной * (применение действия). ((x * f) * g) = (x * (f ◦ g)) (1) (0 * x) = (x * 0) = 0 (2) (x * e) = x (3).
Пополнение программы до GAPS. Теория алгебраической структуры — некоторое множество формул, истинных на этой структуре. ThP — теория Th, в которой все кванторы ограничены новым одноместным предикатом P. Теорема(2012–2013) Пусть система действий A описывается теорией Th1, и Th — теория полугруппы G, и есть гомоморфизм G → A, и P не принадлежит объединению сигнатур. Тогда G можно пополнить действиями A тогда и только тогда, когда теория Th1 ∪ ThP непротиворечива. Длина доказательства 5 страниц, использует теорию моделей и теорию алгебраических систем.
Представление λ-исчисления в GAPS. (x * (y * K)) = y; (x * (y * (z * S)) = ((x * y) * (x * z)). (f * ((g * (h * B)) = (f * (g * h)) (f * ((g * (h * B)) * B)) = ((f * (g * B)) * (h * B)). Поскольку полные по Тьюрингу языки (как традиционные, так и объектные и функциональные) описываются через λ-исчисление, они могут быть описаны как GAPS. За один шаг до этого остановились Böhm, Dezani-Ciancaglini 1972.
Brainfuck-like GAPS. Пусть все строки в алфавите A программы и их соединение — композиция программ (как в языке Brainfuck) e пустая программа = пустая строка. 0 не входит в A и интерпретируется как ошибка. Тогда действие s на t — просто результат применения программы s к данным t. Так что алгебры описывают и языки очень низкого уровня тоже.
Преимущества (полу)групповой семантики. Композиция a ◦ b может пониматься тремя способами: 1. выполняется действие a, а затем b; 2. применяем функцию b к a; 3. строим композицию функций a и b. Все эти интерпретации можно смешивать как угодно. Это главная особенность полугрупп как пространства элементов и действий.
Пример преобразования динамической системы в алгебру. Динамическую систему без диссипации Σ можно рассматривать как функционал, перерабатывающий элемент фазового пространства (начальное значение) в функцию, дающую положение системы в любой заданный момент времени. Уравнения Σ обратимы согласно законам динамики. Она порождает группу сдвигов, элементами которой являются функции λx.(t (xΣ)) сдвига текущего положения системы на t.
Продолжаем описание. Многообразие фазовых траекторий описывается методами алгебраической топологии как комплекс, у которого есть группы гомологий (группы n-мерных циклов из клеток многообразия). Фазовое пространство любой системы относительно некоторой совокупности преобразований координат (все равно, линейных или нет) образует группу преобразований. Если некоторое многообразие обладает симметриями, то они составляют группу. Все эти группы могут использоваться для определения того, в каком качественном состоянии находится система, именно поэтому исследование качественных свойств сложных систем сводится к исследованию порождаемых ими комплексов групп.
А если система диссипативна? Система, в которой ускорение трения задается формулой d2x / dt2 = if |dx / dt |> 0 then − a dx/dt |dx/dt| else 0 fi a > 0 — постоянная, дает группу гомотопий пространства (t, x, dx/dt) как конуса над x. Еще проще описать полугруппой, получаемой отождествлением всех точек фазового пространства, в которых система останавливается более чем за k секунд, от k до k − 1 и так далее до 0.
Полугруппа. Произведение n ◦ m — перейти к состояниям, получающимся через m секунд. Нильпотентная полугруппа с элементами {k, k − 1, . . . , 1, 0} и правилом умножения n ◦ m = if n > m then n − m else 0 fi. Если нас интересуют также области, в которых заканчивается процесс, то полугруппу легко модифицировать и на этот случай с помощью конструкции подпрямого произведения.
Algebra of fully invertible programs (AFIP)). Добавляем обращение: x ◦ (x * M) = e (x * M) ◦ x = e (4). Тогда ◦ задает группу, а M вычисляет обратный элемент. Для «железячников». Группа представляет кристаллики, * — их соединения.
Доказательство обратимости действий. Лемма. Отображение λx.(x * f) биективно для любого f. Доказательство. Инъективность. Пусть (x * f) = (y * f). Тогда ((x * f) * (f * M)) = ((y * f) * (f * M)) (x * (f ◦ (f * M))) = ((y * (f ◦ (f * M))) (x * e) = (y * e) = x = y. Сюръективность. Найдем для каждого x и f такое y, что (y * f) = x. ((x * f) * (f * M)) = ((y * f) * (f * M)) ((x * (f * M)) * f) = (x * ((f * M) ◦ f)) = (x * e) = x.
Когда группа становится алгеброй. Пусть группа G не является группой порядка 2. Пусть G0 — ее подгруппа, и не являющаяся группой порядка 2 (хотя она может содержать элементы порядка 2). Пусть X♠ замыкание множества X относительно групповых операций и многозначной частично-определенной операции извлечения корней нечетной степени из неединичных элементов внутри группы G. Существует алгебра AFIP G0 такая, что для всех f ∈ G0 (x ? f) = (x ◦ f) тогда и только тогда, когда есть элемент порядка 2, не входящий в G0 ♠, и не являющийся квадратом никакого элемента группы.
Примеры. Группа Z4 не может быть пополнена до AFIP, поскольку из единственного элемента второго порядка 2 извлекается корень: 2 = 1 ◦ 1. По аналогичным причинам не пополнимы R+ и R×. А Z6 может быть пополнена: λx.(x * 3) = λx.(x * 1) = λx.(x * 5) = λx. x−1 , λx.(x * 0) = λx.(x * 2) = λx.(x * 4) = λx. x. Могут быть пополнены все группы Z4n+2 и только они.
Пополнение произвольной группы. Превратим группу Z2 × G в AFIP Положим hx, ai*h0, bi = hx, a ◦ bi hx, ai*h1, ei = x, a−1 . Тогда имеем hx, ai * h1, bi = hx, ai ? (h1, ei ◦ h0, bi) = ((hx, ai * h1, ei) * h0, bi) = x, a−1 * h0, bi = x, a−1 ◦ b . (5)
Представление условного оператора. Пусть G — исходная группа команд, H — группа значений альтернатив. Z2 × G × G × H с операцией hz, a1, b1, c1i ◦ h0, a2, b2, c2i = hz, a1 ◦ a2, b1 ◦ b2, c1 ◦ c2i hz, a1, b1, c1i ◦ h1, a2, b2, c2i = hz ⊕ 1, a1 ◦ b2, b1 ◦ a2, c1 ◦ c2i (6) представляемая как (G × G) o (Z2 × H).
Математические задачи. Классификация конечных AFIP хотя бы над простейшими конечными группами. Методы декомпозиции AFIP. Приближение бесконечных AFIP последовательностями конечных (алгебраический аналог метода сеток) Алгебраические структуры «почти обратимых» действий: в реальности каждая программа заканчивается необратимым действием чтения результатов. Кроме того, система может быть обратимой на подпространствах с необратимым переключением в особых точках.
Логические задачи. Исследование конструктивной пропозициональной логики AFIP. Основное семантическое понятие “элемент a реализует формулу A” 1. arA ⇒ B , ∀b ∈ G(brA ⊃ (b ? a)rB). Итак, a преобразует решения A в решения B. 2. a ◦ brA&B , arA ∧ brB. Решение B применяется к решению A. 3. ar ∼ A , a−1rA. a аннулирует решение A либо препятствует ему.
Алгебра полуобратимых программ. Рассмотрим полугруппу с правыми обратными. (0 * x) = (x * 0) = 0 (7) f в минус 1= 0 ⊃ (f * M) = f −1 (8) ∀x, f((x ? f) в минус 1= 0 ⊃ (x * (f ◦ f −1 )) = x ◦ f ◦ f −1 ) (9) Тогда все действия у нас полуобратимы (инъективны). В такой алгебре 0 представляет ошибку, а делители нуля — программы, которые по отдельности работают, а в сборке — нет.
Понятия из теории полугрупп. Элементы a и b взаимно обратны, если a ◦ b ◦ a = a, b ◦ a ◦ b = b. Полугруппа инверсная, если у каждого ненулевого элемента есть единственный обратный. Тогда для обратного используется традиционное обозначение a в−1. Элемент a полный, если a ◦ a в −1 = e. Если a не равно 0, b не равно 0, a ◦ b = 0, то a называется левым делителем нуля, b — правым. a — делитель нуля, если есть такие b и c, что a ◦ b ◦ c = 0.
Понятия из теории полугрупп 2. Частичная функция — такая функция, что для некоторого ненулевого a (a * f) = 0. В инверсной полугруппе a является ограничением b (a меньше или равно b), если a ◦ b в−1= a ◦ a в−1. a — частичная единица, если a = b ◦ b в−1 для некоторого b не равно 0.
Результаты

Этих результатов в литературе нет
Результаты 2

Эти результаты или эквивалентные им есть в литературе.
Частичная инъективность. ∀a, b, f ((a*f) = (b*f) ≡ (a?(f◦f в −1 )) = (b*(f◦f в −1 ))). Очевидно. Полной инъективности ожидать нельзя. Пусть f определена лишь на натуральных числах, y совпадает с x на натуральных числах, но различается на отрицательных, хотя все функции инъективны. Тогда (x ◦ f) = (y ◦ f)&x не равно y.
Ещё результаты. ∀x, f ((x * f) = 0 ≡ x ◦ f = 0). Доказательство. Пусть (x * f) = 0, f 6= 0. Тогда 0 = (0?f в −1 ) = ((x*f)*f в −1 ) = ((x*(f◦f в −1 )) = x◦f◦f в −1 = Повторяя эту последовательность преобразований в обратную сторону, получаем вторую часть доказываемой эквивалентности. Лемма. Каждая инверсная полугруппа с нулем, единицей и хотя бы одним элементом второго порядка, может быть продолжена до APIP. Лемма. Каждая инверсная полугруппа с нулем, единицей и хотя бы одним элементом второго порядка, может быть продолжена до APIP. Лемма. Пусть G0 — подмоноид инверсной полугруппы с нулем G, не совпадающий с нею самой и с {0, e} и в G \ G0 есть хотя бы один элемент второго порядка. Тогда его можно продолжить до APIP G0, такой, что для всех f ∈ G0 (x * f) = (x ◦ f).
Полупрямое произведение. В программах обычно целесообразно выделять команды и данные. Этим условиям удовлетворяет конструкция полупрямого произведения, известная для групп и обобщаемая здесь на полугруппы и программные алгебры. Полупрямое произведение полугруппы команд C и полугруппы данных D есть полугруппа C o D, носитель которой C × D, а операция умножения определяется следующим образом. Задан гомоморфизм ϕ : C → Hom(D, D) полугруппы команд в полугруппу гомоморфизмов полугруппы данных. hc1, d1i ◦ hc2, d2i = hc1 ◦ c2, d1 ◦ (d2 (c2 ϕ))i. Полупрямое произведение программных алгебр C и D определяется аналогично с дополнительным условием на *: <c1, d1> * <c2, d2> = <c1 * c2, d1 * (d2 (c2 ϕ))>.
Алгебра завершающихся программ (ANP). Пусть G строго нильпотентная полугруппа, т. е. такая, что для любой последовательности ai существует n, при котором П n i=1 ai = 0. Тогда все последовательности действий также ведут к 0 и любой процесс заканчивается за конечное число шагов.
Были ли алгебры программ раньше? Начиная с 60-х годов. Маурер и Глушков. Эти два направления развиваются и до сих пор. Но все алгебры в качестве примитивов рассматривали алгебраические образы операторов языка программирования (как минимум, условного и цикла). У нас ортогональная система: программы классифицируем по свойствам, а не по операторам.
- Непейвода Н.Н.: Уроки конструктивизма. Geidelberg: Lambert Academic Publishing, 98 pp. (2011)
- Непейвода Н.Н.: Реверсивные конструктивные логики. Логические исследования, 15, 150–168 (2009)
- Непейвода А. Н.: О сюрьективной импликации в реверсивной логике. VI Смирновские чтения по логике (2009)
- Непейвода А. Н. Элементы реверсивных вычислений Управление большими системами труды VI всероссийской школы-семинара молодых ученых, Ижевск (2009)
- Непейвода А. Н.: О реверсивной альтернативе традиционным вычислениям. Трехмерная визуализация научной, технической и социальной реальности. Технологии высокополигонального моделирования : труды Второй междунар. конф., Ижевск (2010).
- Непейвода А. Н.: Функциональное программирование над группой. Системный анализ и семиотическое моделирование: труды первой всероссийской конференции, 2011, Казань (2011)
- Nepejvoda N. N. Reversivity, reversibility and retractability. Third Int. Workshop on Metacomputation. Pereslavl, 2012, pp 203–227.
- Непейвода Н. Н. От численного моделирования к алгебраическому РАСО‘2012 т. 1 М.: 2012 стр. 93–103.
- Непейвода А Н. Реверсивные вычисления: обзор мирового опыта РАСО‘2012 т. 2 М.: 2012 ISBN стр. 129–142.
- Непейвода Н. Н. Абстрактные алгебры различных классов программ. Аппликативные Вычислительные Системы 3-я международная конференция АВС 2012 Москва, С. 103–128.