AI -1

techworldthink

Q1. Applications of artificial intelligence

Robotic vehicles

Speech recognition

Autonomous planning and scheduling

Game playing

Spam fighting

Logistics planning

Robotics

Machine translation

Agriculture

Cybersecurity

Finance

Healthcare

Artificial general intelligence.
Planning.
Computer vision.
General game playing.
Knowledge reasoning.
Machine learning.
Natural language processing.
Robotics.

Q2. Solve the cryptarithmetic problem

S E N D + M O R E = M O N E Y

Cryptarithmetic Problem

Cryptarithmetic Problem is a type of constraint satisfaction problem where the game is about digits and its unique replacement either with alphabets or other symbols. In cryptarithmetic problem, the digits (0-9) get substituted by some possible alphabets or symbols. The task in cryptarithmetic problem is to substitute each digit with an alphabet to get the result arithmetically correct.

We can perform all the arithmetic operations on a given cryptarithmetic problem.

The rules or constraints on a cryptarithmetic problem are as follows:

There should be a unique digit to be replaced with a unique alphabet.
The result should satisfy the predefined arithmetic rules, i.e., 2+2 =4, nothing else.
Digits should be from 0-9 only.
There should be only one carry forward, while performing the addition operation on a problem.
The problem can be solved from both sides, i.e., lefthand side (L.H.S), or righthand side (R.H.S)

Let’s understand the cryptarithmetic problem as well its constraints better with the help of an example:

Given a cryptarithmetic problem, i.e., S E N D + M O R E = M O N E Y

In this example, add both terms S E N D and M O R E to bring M O N E Y as a result.

Follow the below steps to understand the given problem by breaking it into its subparts:

Starting from the left hand side (L.H.S) , the terms are S and M. Assign a digit which could give a satisfactory result. Let’s assign S->9 and M->1.

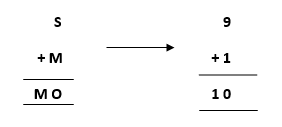
Hence, we get a satisfactory result by adding up the terms and got an assignment for O as O->0 as well.

Now, move ahead to the next terms E and O to get N as its output.

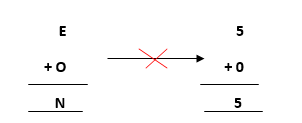
Adding E and O, which means 5+0=0, which is not possible because according to cryptarithmetic constraints, we cannot assign the same digit to two letters. So, we need to think more and assign some other value.

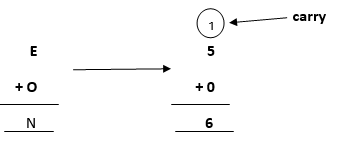
Note: When we will solve further, we will get one carry, so after applying it, the answer will be satisfied.

Further, adding the next two terms N and R we get,

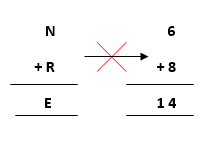
But, we have already assigned E->5. Thus, the above result does not satisfy the values

because we are getting a different value for E. So, we need to think more.

Again, after solving the whole problem, we will get a carryover on this term, so our answer will be satisfied.

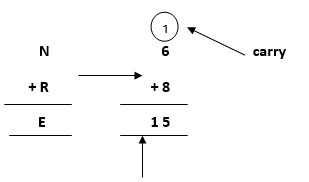
where 1 will be carry forward to the above term

Let’s move ahead.

Again, on adding the last two terms, i.e., the rightmost terms D and E, we get Y as its result.

where 1 will be carry forward to the above term

Keeping all the constraints in mind, the final resultant is as follows:

Below is the representation of the assignment of the digits to the alphabets.

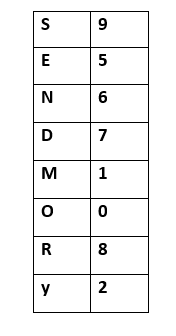
Q3. Iterative Deepening Search(IDS) or Iterative Deepening Depth First Search(IDDFS)

There are two common ways to traverse a graph, BFS and DFS. Considering a Tree (or Graph) of huge height and width, both BFS and DFS are not very efficient due to following reasons.

DFS first traverses nodes going through one adjacent of root, then next adjacent. The problem with this approach is, if there is a node close to root, but not in first few subtrees explored by DFS, then DFS reaches that node very late. Also, DFS may not find shortest path to a node (in terms of number of edges).

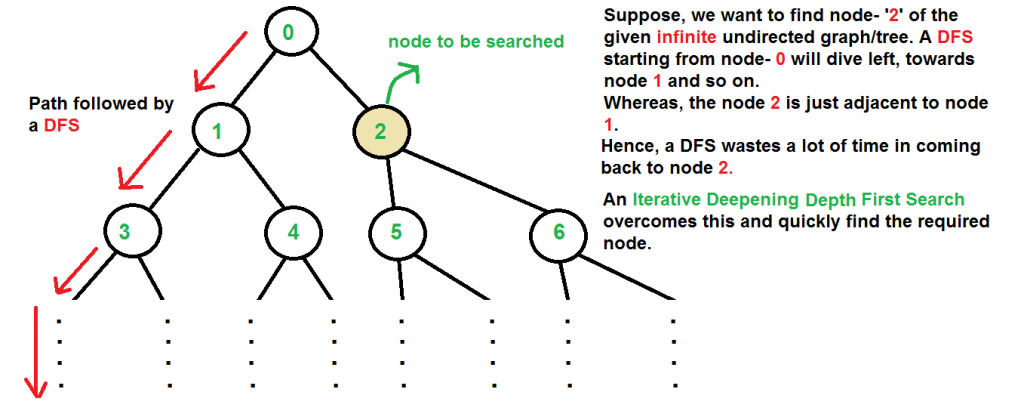
BFS goes level by level, but requires more space. The space required by DFS is O(d) where d is depth of tree, but space required by BFS is O(n) where n is number of nodes in tree (Why? Note that the last level of tree can have around n/2 nodes and second last level n/4 nodes and in BFS we need to have every level one by one in queue).

IDDFS combines depth-first search’s space-efficiency and breadth-first search’s fast search (for nodes closer to root).

How does IDDFS work?

IDDFS calls DFS for different depths starting from an initial value. In every call, DFS is restricted from going beyond given depth. So basically we do DFS in a BFS fashion.

An important thing to note is, we visit top level nodes multiple times. The last (or max depth) level is visited once, second last level is visited twice, and so on. It may seem expensive, but it turns out to be not so costly, since in a tree most of the nodes are in the bottom level. So it does not matter much if the upper levels are visited multiple times.

There can be two cases-

a) When the graph has no cycle:

This case is simple. We can DFS multiple times with different height limits.

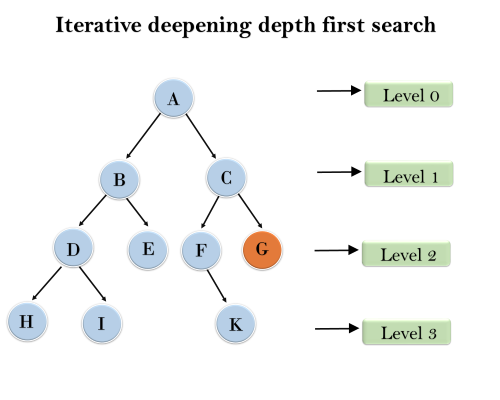
1'st Iteration-----> A

2'nd Iteration----> A, B, C

3'rd Iteration------>A, B, D, E, C, F, G

4'th Iteration------>A, B, D, H, I, E, C, F, K, G

In the fourth iteration, the algorithm will find the goal node.

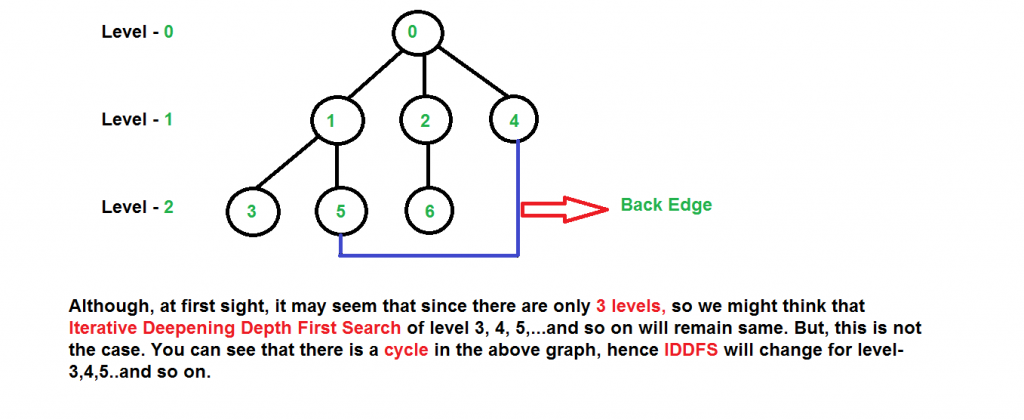
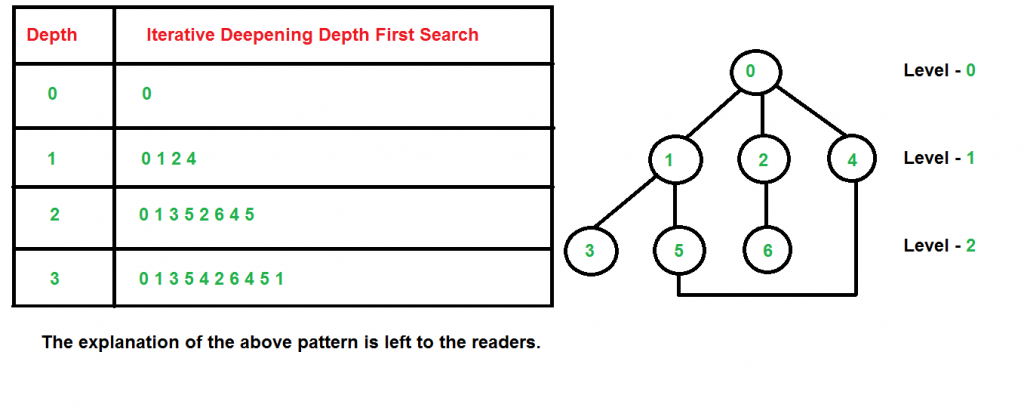
b) When the graph has cycles.

This is interesting as there is no visited flag in IDDFS

Q4. Disadvantages of hill climbing

Hill Climbing is a heuristic search used for mathematical optimization problems in the field of Artificial Intelligence.

Given a large set of inputs and a good heuristic function, it tries to find a sufficiently good solution to the problem. This solution may not be the global optimal maximum.

In the above definition, mathematical optimization problems implies that hill-climbing solves the problems where we need to maximize or minimize a given real function by choosing values from the given inputs. Example-Travelling salesman problem where we need to minimize the distance traveled by the salesman.
‘Heuristic search’ means that this search algorithm may not find the optimal solution to the problem. However, it will give a good solution in reasonable time.
A heuristic function is a function that will rank all the possible alternatives at any branching step in search algorithm based on the available information. It helps the algorithm to select the best route out of possible routes

Disadvantages of Hill Climbing

It is not an efficient method.
It is not suited to problems where the value of the heuristic function drops off suddenly when the solution may be in sight.
It is a local method as it looks at the immediate solution and decides about the next step to be taken rather than exploring all consequences before taking a move.
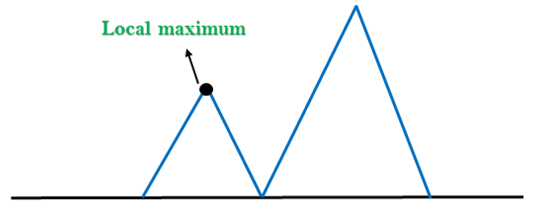
Local Maximum: A local maximum is a peak state in the landscape which is better than each of its neighboring states, but there is another state also present which is higher than the local maximum.

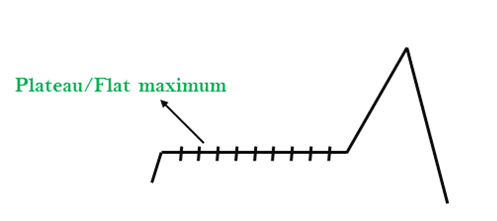
Plateau: A plateau is the flat area of the search space in which all the neighbor states of the current state contains the same value, because of this algorithm does not find any best direction to move. A hill-climbing search might be lost in the plateau area.

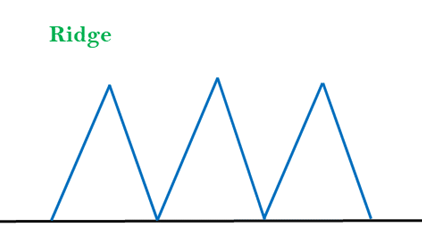
Ridges: A ridge is a special form of the local maximum. It has an area which is higher than its surrounding areas, but itself has a slope, and cannot be reached in a single move

Q5. Two player zero sum game

Zero-sum: A zero-sum game is defined as one where the total payoff to all players is the same for every instance of the game.

In zero-sum game, every game has the total payoff(consequence) of either 0 + 1

Example 1: Chess The best known example of a game considered in AI is chess.

In chess, the outcome is a win, loss, or draw, with values +1, 0, or 1/2. It is a zero-sum game because every game has the total payoff of either 0 + 1, 1 + 0 or 1/2 + 1/2.

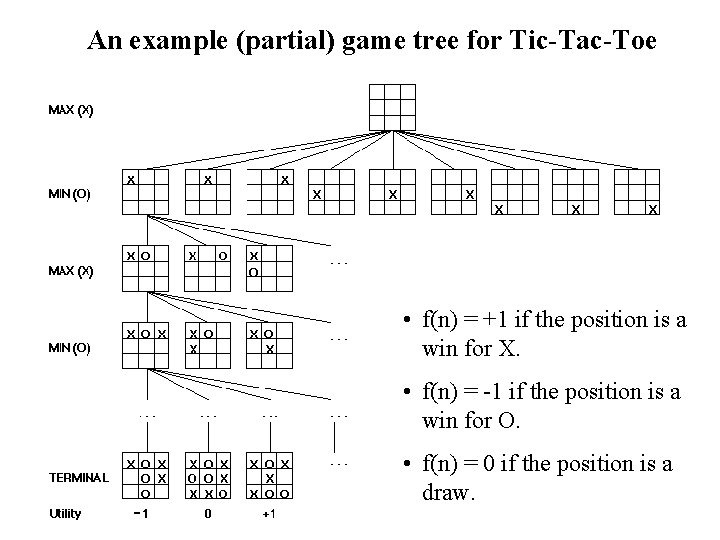
Example 2: Tic-tac-toe

Tic-tac-toe or noughts and crosses is a paper-and-pencil game for two players, X and O, who take turns marking the spaces in a 3 × 3 grid. The player who succeeds in placing three of his/her marks in a diagonal, horizontal, or vertical row is the winner

Initial state(S0): which specifies how the game is set up at the start

TO-MOVE(s): The player whose turn it is to move in state s .

ACTIONS(s) : The set of legal moves in state s.

RESULT (s, a): The transition model, which defines the state resulting from taking action a in state s.

IS-TERMINAL(s): A terminal test, which is true when the game is over and false otherwise.States where the game has ended are called terminal states.

UTILITY(s, p): A utility function (also called an objective function or payoff function),which defines the final numeric value to player p when the game ends in terminal state s. In chess, the outcome is a win, loss, or draw, with values 1, 0, or ½. Some games have a wider range of possible outcomes—for example, the payoffs in backgammon range from 0 to 192.

Consider Tic-tac-toe game, MIN and MAX are players in game

MAX plays by placing an X and MIN plays by placing an O in a cell in the

grid

Play alternates between Max placing an X and Min placing an O

High values are assumed to be good for MAX and bad for MIN (That is

how the players get their names)

Since it is a zero-sum game, one player’s gain is opponent’s loss.

The player who is trying to maximize the gain is called the maximizing

player(MAX) and the player who is trying to minimize the loss is called

the minimizing player(MIN).

“minimax strategy” is used to solve these types of problem; the player

MAX chooses a move that would maximize his minimum gain and player

MIN chooses a move which would minimize his maximum loss. The

procedure based on this strategy known as the “Minimax algorithm”

Q6. Conceptual dependencies

There are several knowledge representation systems such as the following.

• Semantic networks

• Frames

• Conceptual dependencies

• System based on logic

Conceptual dependency (CD) is a theory of knowledge representation developed by Roger Schank and his teammates at Yale University in the 1970’s. It is a theory to represent natural language sentences in such way that:

• It is independent of the language in which the sentences are stated.

• It facilitates drawing inferences from sentences.

The model uses the following basic representational tokens

real world objects, each with some attributes.
real world actions, each with attributes
times
locations

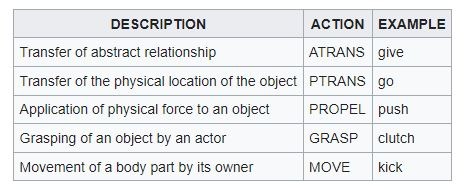
A sentence such as "John gave a book to Mary" is then represented as the action of an ATRANS on two real world objects John and Mary.

Q7. Inference rules in FOPL(First order predicate logic)

In first order predicate logic, also called simply predicate logic, we are

concerned with statements which will be applicable to the elements in some

set of objects and about the truth values of such statements.

Rules

Universal instantiation (UI)

Existential instantiation (EI)

Generalised modus ponens (GMP)

Resolution inference rule

Q8. Components of a planning system

The following are the components of a planning system:

1. Choosing rules to apply

2. Applying rules

3. Detecting a solution

4. Detecting dead ends

5. Repairing an almost correct solution

Q9. Role of Expert System

Expert systems of today support many problem solving activities such as decision making, knowledge fusing, designing, and planning, forecasting, regulating, controlling, monitoring, identifying, diagnosing, prescribing, interpreting, explaining, training etc.

The basic role of an expert system is to replicate a human expert and replace him or her in a problem-solving activity.

Four interactive roles form the activities of the expert system:

diagnosing
interpreting
predicting
instructing

Q10. fuzzy Operations

Let A and B be two fuzzy sets in a universe U.

1. Equality A and B are said to be equal, denoted by A = B, if µA(x) = µB(x) for all x in U.

2. Union The union of A and B, denoted by A ∪ B, is the fuzzy set C whose membership function is defined by µC(x) = max{µA(x), µB(x)}, x ∈ U.

3. Intersection The intersection of A and B, denoted by A∩B, is the fuzzy set D whose membership function is defined by µD(x) = min{µA(x), µB(x)}, x ∈ U.

4. Complement The complement of A, denoted by A, is the fuzzy set E whose membership function is defined by µE(x) = 1 − µA(x), x ∈ U.